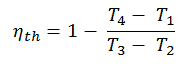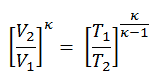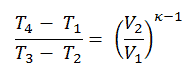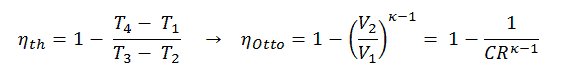Taux de compression – Moteur Otto
Le taux de compression , CR , est défini comme le rapport entre le volume au point mort bas et le volume au point mort haut. C’est une caractéristique clé pour de nombreux moteurs à combustion interne. Dans la section suivante, nous montrerons que le taux de compression détermine le rendement thermique du cycle thermodynamique utilisé du moteur à combustion. En général, on souhaite avoir un taux de compression élevé, car cela permet à un moteur d’atteindre un rendement thermique supérieur.
Par exemple, supposons un cycle d’Otto avec un taux de compression de CR = 10: 1. Le volume de la chambre est de 500 cm³ = 500 × 10 -6 m 3 (0,5 l) avant la course de compression. Pour ce moteur un ll requis volumes sont connus:
- V 1 = V 4 = V max = 500 × 10 -6 m 3 (0,5 l)
- V 2 = V 3 = V min = V max / CR = 55,56 × 10 -6 m 3
Notez que (V max – V min ) x nombre de cylindres = cylindrée totale du moteur.
Efficacité thermique pour le cycle d’Otto
En général , le rendement thermique , η e , d’un moteur thermique est définie comme étant le rapport entre le travail qu’elle fait, W , à la chaleur d’ entrée à la température élevée, Q H .
Le rendement thermique , η e , représente la fraction de la chaleur , Q H , qui est converti pour fonctionner . Etant donné que l’ énergie est conservée en fonction de la première loi de la thermodynamique et de l’ énergie ne peut pas être converties pour fonctionner complètement, l’apport de chaleur, Q H , doit être égal au travail effectué, W, ainsi que la chaleur qui doit être dissipée sous forme de chaleur perdue Q C dans le environnement. Par conséquent, nous pouvons réécrire la formule pour l’efficacité thermique comme suit:
La chaleur absorbée se produit pendant la combustion du mélange carburant-air, lorsque l’étincelle se produit, à peu près à volume constant. Puisqu’au cours d’un processus isochore, aucun travail n’est effectué par ou sur le système, la première loi de la thermodynamique dicte ∆U = ∆Q. Par conséquent, la chaleur ajoutée et rejetée est donnée par:
Q add = mc v (T 3 – T 2 )
Q out = mc v (T 4 – T 1 )
En substituant ces expressions à la chaleur ajoutée et rejetée dans l’expression pour l’efficacité thermique, on obtient:
Nous pouvons simplifier l’expression ci-dessus en utilisant le fait que les processus 1 → 2 et de 3 → 4 sont adiabatiques et pour un processus adiabatique la formule p, V, T suivante est valide:
On peut déduire que:
Dans cette équation, le rapport V 1 / V 2 est appelé taux de compression CR . Lorsque nous réécrivons l’expression de l’efficacité thermique en utilisant le taux de compression, nous concluons que l’ efficacité thermique du cycle d’Otto standard de l’ air est fonction du taux de compression et de κ = c p / c v .
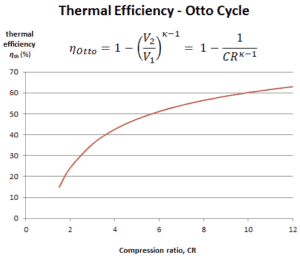
C’est une conclusion très utile, car il est souhaitable d’atteindre un taux de compression élevé pour extraire plus d’énergie mécanique d’une masse donnée de mélange air-carburant. Un taux de compression plus élevé permet d’atteindre la même température de combustion avec moins de carburant, tout en prolongeant le cycle de détente. Cela crée plus de puissance mécanique et abaisse la température d’échappement . L’abaissement de la température d’échappement provoque l’abaissement de l’énergie rejetée dans l’atmosphère. Cette relation est représentée sur la figure pour κ = 1,4, représentant l’air ambiant.
……………………………………………………………………………………………………………………………….
Cet article est basé sur la traduction automatique de l’article original en anglais. Pour plus d’informations, voir l’article en anglais. Pouvez vous nous aider Si vous souhaitez corriger la traduction, envoyez-la à l’adresse: translations@nuclear-power.com ou remplissez le formulaire de traduction en ligne. Nous apprécions votre aide, nous mettrons à jour la traduction le plus rapidement possible. Merci