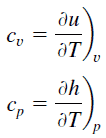Was ist der erste Hauptsatz der Thermodynamik – Definition

Erster Hauptsatz der Thermodynamik

Die Zunahme der inneren Energie eines geschlossenen Systems entspricht der dem System zugeführten Wärme abzüglich der von ihm geleisteten Arbeit.

∆E _int = Q – W.

Dies ist der erste Hauptsatz der Thermodynamik und es ist das Prinzip der Erhaltung der Energie , was bedeutet , dass Energie kann weder erzeugt noch vernichtet werden , sondern in verschiedene Formen als Fluid umgewandelt in dem Steuerraum wird untersucht.

Es ist das wichtigste Gesetz für die Analyse der meisten Systeme und das Gesetz, das quantifiziert, wie Wärmeenergie in andere Energieformen umgewandelt wird . Daraus folgt, dass Perpetual-Motion-Maschinen der ersten Art unmöglich sind.

Prinzip der Energieeinsparung

Eine der wunderbarsten Eigenschaften des Universums ist, dass Energie von einem Typ in einen anderen umgewandelt und von einem Objekt auf ein anderes übertragen werden kann. Darüber hinaus ist die Gesamtenergiemenge immer gleich , wenn sie von einem Typ zu einem anderen transformiert und von einem Objekt zu einem anderen übertragen wird . Es ist eine der elementaren Eigenschaften des Universums.

In der Thermodynamik wird das Energiekonzept erweitert, um andere beobachtete Änderungen zu berücksichtigen, und das Prinzip der Energieerhaltung wird um eine Vielzahl von Arten der Interaktion von Systemen mit ihrer Umgebung erweitert. Die Energie eines geschlossenen Systems kann nur durch Energieübertragung durch Arbeit oder Wärme verändert werden . Basierend auf den Experimenten von Joule und anderen ist ein grundlegender Aspekt des Energiekonzepts, dass Energie erhalten bleibt. Dieses Prinzip ist als  erster Hauptsatz der Thermodynamik bekannt . Der erste Hauptsatz der Thermodynamik kann in verschiedenen Formen geschrieben werden:

In Worten:

Gleichungsform:

∆E _int = Q – W.

Dabei steht E _int für die innere Energie des Materials, die nur vom Zustand des Materials (Temperatur, Druck und Volumen) abhängt . Q ist die Netto-Wärmezufuhr an das System und W ist das Netz durch geleistete Arbeit das System. Wir müssen vorsichtig und konsequent sein, wenn wir die Vorzeichenkonventionen für Q und W befolgen. Da W in der Gleichung die vom System geleistete Arbeit ist, ist W negativ und E _int nimmt zu , wenn am System gearbeitet wird.

In ähnlicher Weise ist Q positiv für die dem System zugeführte Wärme. Wenn also Wärme das System verlässt, ist Q negativ. Dies sagt uns Folgendes: Die interne Energie eines Systems steigt tendenziell an, wenn Wärme vom System absorbiert wird oder wenn positive Arbeit am System geleistet wird. Umgekehrt neigt die interne Energie dazu, abzunehmen, wenn das System Wärme verliert oder wenn negative Arbeiten am System ausgeführt werden. Es muss hinzugefügt werden, dass Q und W pfadabhängig sind, während E _{int pfadunabhängig} ist.

Differentialform:

dE _int = dQ – dW

Die interne Energie E _int eines Systems nimmt tendenziell zu, wenn Energie als Wärme Q hinzugefügt wird, und nimmt tendenziell ab, wenn Energie als vom System geleistete Arbeit W verloren geht.

Erstes Gesetz in Bezug auf die Enthalpie dH = dQ + Vdp

Die Enthalpie ist definiert als die Summe aus der seinen inneren Energie E plus das Produkt des Druck p und Volumen V . In vielen thermodynamischen Analysen erscheint die Summe der inneren Energie U und des Produkts aus Druck p und Volumen V, daher ist es zweckmäßig, der Kombination einen Namen, eine Enthalpie und ein eindeutiges Symbol H zu geben.

H = U + pV

Siehe auch: Enthalpie

Der erste Hauptsatz der Thermodynamik in Bezug auf die Enthalpie zeigt uns, warum Ingenieure die Enthalpie in thermodynamischen Kreisprozessen verwenden (z. B. Brayton-Zyklus oder Rankine-Zyklus ).

Die klassische Form des Gesetzes ist die folgende Gleichung:

dU = dQ – dW

In dieser Gleichung dW gleich dW = pdV und ist bekannt als die Grenz Arbeit .

Da H = U + pV ist , ist dH = dU + pdV + Vdp und wir setzen dU = dH – pdV – Vdp in die klassische Form des Gesetzes ein:dH – pdV – Vdp = dQ – pdV

Wir erhalten das Gesetz in Bezug auf die Enthalpie:

dH = dQ + Vdp

oder

dH = TdS + Vdp

In dieser Gleichung ist der Begriff Vdp eine Flussprozessarbeit. Diese Arbeit,   Vdp , wird für Open-Flow-Systeme wie eine Turbine oder eine Pumpe verwendet, bei denen ein „dp“ vorliegt , dh eine Druckänderung. Es gibt keine Änderungen in der Lautstärke . Wie zu sehen ist, vereinfacht diese Form des Gesetzes die Beschreibung der Energieübertragung . Bei konstantem Druck entspricht die Enthalpieänderung der Energie , die durch Erhitzen aus der Umgebung übertragen wird:

Isobarer Prozess (Vdp = 0):

dH = dQ      →      Q = H ₂ – H ₁

Bei konstanter Entropie , dh im isentropischen Prozess, entspricht die Enthalpieänderung der am oder vom System durchgeführten Flussprozessarbeit :

Isentropischer Prozess (dQ = 0):

dH = Vdp      →      W = H ₂ – H ₁

Es ist offensichtlich, dass es bei der Analyse sowohl der in der Energietechnik verwendeten thermodynamischen Kreisprozessen, dh des Brayton-Zyklus als auch des Rankine-Zyklus, sehr nützlich sein wird.

Beispiel: Erster Hauptsatz der Thermodynamik und des Brayton-Zyklus

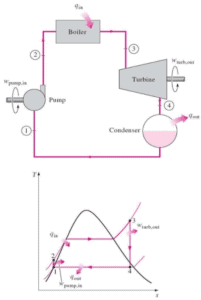
Nehmen wir den idealen Brayton-Zyklus an , der die Funktionsweise einer Wärmekraftmaschine mit konstantem Druck beschreibt . Moderne Gasturbinentriebwerke und luftatmende Strahltriebwerke folgen ebenfalls dem Brayton-Zyklus. Dieser Zyklus besteht aus vier thermodynamischen Prozessen:

1. 

   isentropische Kompression – Umgebungsluft wird in den Kompressor gesaugt und dort unter Druck gesetzt (1 → 2). Die für den Kompressor erforderliche Arbeit ist gegeben durch W _C = H ₂ – H ₁ .

2. isobare Wärmezufuhr – Die Druckluft strömt dann durch eine Brennkammer, in der Kraftstoff verbrannt und Luft oder ein anderes Medium erwärmt wird (2 → 3). Es ist ein Prozess mit konstantem Druck, da die Kammer zum Ein- und Ausströmen geöffnet ist. Die hinzugefügte Nettowärme ist gegeben durch Q _add = H ₃ – H ₂
3. isentropische Expansion – Die erwärmte Druckluft dehnt sich dann auf der Turbine aus und gibt ihre Energie ab. Die von der Turbine geleistete Arbeit ist gegeben durch W _T = H ₄ – H ₃
4. isobare Wärmeabgabe – Die Restwärme muss abgeführt werden, um den Kreislauf zu schließen. Die abgegebene Nettowärme ist gegeben durch Q _re = H ₄ – H ₁

Wie zu sehen ist, können wir solche Kreisprozessen (ähnlich für den Rankine-Zyklus ) unter Verwendung von Enthalpien beschreiben und berechnen (z. B. thermodynamische Effizienz) .

Innere Energie

In der Thermodynamik wird innere Energie (auch als Wärmeenergie bezeichnet ) als die Energie definiert, die mit mikroskopischen Energieformen verbunden ist . Es handelt sich um eine umfangreiche Menge , die von der Größe des Systems oder der Menge der darin enthaltenen Substanz abhängt. Die SI-Einheit der inneren Energie ist das Joule (J) . Es ist die im System enthaltene Energie, ausgenommen die kinetische Bewegungsenergie des gesamten Systems und die potentielle Energie des Systems. Mikroskopische Energieformen umfassen solche aufgrund von Rotation , Vibration, Translation und Wechselwirkungenunter den Molekülen einer Substanz. Keine dieser Energieformen kann direkt gemessen oder bewertet werden, es wurden jedoch Techniken entwickelt, um die Änderung der Gesamtsumme all dieser mikroskopischen Energieformen zu bewerten.

Zusätzlich kann Energie in den chemischen Bindungen zwischen den Atomen gespeichert werden, aus denen die Moleküle bestehen. Dieser Energiespeicher auf atomarer Ebene umfasst Energie, die mit Elektronenorbitalzuständen, Kernspin und Bindungskräften im Kern verbunden ist.

Mikroskopische Energie

Interne Energie beinhaltet Energie im mikroskopischen Maßstab . Es kann in mikroskopische potentielle Energie, U- _Pot und mikroskopische kinetische Energie, U- _Kin , Komponenten unterteilt werden:

U = U _Topf + U _Kin

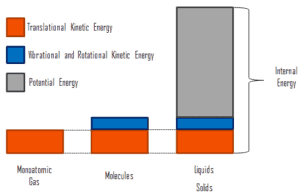wobei die mikroskopische kinetische Energie U _kin die Bewegungen aller Partikel des Systems in Bezug auf den Schwerpunktrahmen umfasst. Für ein ideales einatomiges Gas ist dies nur die translatorische kinetische Energie der linearen Bewegung der Atome. Monoatomare Partikel drehen oder vibrieren nicht. Das Verhalten des Systems wird durch die kinetische Theorie der Gase gut beschrieben. Die kinetische Theorie basiert auf der Tatsache, dass während einer elastischen Kollision zwischen einem Molekül mit hoher kinetischer Energie und einem Molekül mit niedriger kinetischer Energie ein Teil der Energie auf das Molekül mit niedriger kinetischer Energie übertragen wird. Für mehratomige Gase gibt es jedoch Rotations- undauch kinetische Schwingungsenergie .

Die mikroskopische potentielle Energie U _pot beinhaltet die chemischen Bindungen zwischen den Atomen, aus denen die Moleküle bestehen, die Bindungskräfte im Kern und auch die physikalischen Kraftfelder innerhalb des Systems (z. B. elektrische oder magnetische Felder).

In Flüssigkeiten und Feststoffen gibt es einen signifikanten Anteil der potentiellen Energie, die mit den intermolekularen Anziehungskräften verbunden ist .

Hitze und Arbeit

Wir haben gesehen , dass die innere Energie mit ändert sich Q , die das ist Netto-Wärmezufuhr an das System und W , was das ist Netto-Arbeit erledigt das System. Wir untersuchen nun, wie die Arbeit und die Wärme, die dem System während eines thermodynamischen Prozesses zugeführt wird, von den Einzelheiten des Prozesses abhängen.

Wärme in der Thermodynamik

Während sich innere Energie auf die Gesamtenergie aller Moleküle im Objekt bezieht, ist Wärme die Energiemenge, die aufgrund ihres Temperaturunterschieds spontan von einem Körper zum anderen fließt . Wärme ist eine Energieform, aber es ist Energie auf dem Transportweg . Wärme ist keine Eigenschaft eines Systems. Die Energieübertragung als Wärme erfolgt jedoch auf molekularer Ebene infolge eines Temperaturunterschieds .

Stellen Sie sich einen Metallblock mit hoher Temperatur vor, der aus Atomen besteht, die stark um ihre Durchschnittspositionen schwingen. Bei niedrigen Temperaturen schwingen die Atome weiter, jedoch mit geringerer Intensität . Wenn ein heißerer Metallblock mit einem kühleren Block in Kontakt gebracht wird, geben die stark oszillierenden Atome am Rand des heißeren Blocks ihre kinetische Energie an die weniger oszillierenden Atome am Rand des kühlen Blocks ab. In diesem Fall findet eine Energieübertragung zwischen diesen beiden Blöcken statt und durch diese zufälligen Vibrationen fließt Wärme vom heißeren zum kühleren Block.

Wenn zwei Objekte in thermischen Kontakt gebracht werden , fließt im Allgemeinen Wärme zwischen ihnen, bis sie sich im Gleichgewicht befinden . Wenn ein Temperaturunterschied besteht, fließt die Wärme spontan vom wärmeren System zum kälteren System . Die Wärmeübertragung erfolgt durch Wärmeleitung oder durch Wärmestrahlung . Wenn der Wärmefluss stoppt , haben sie angeblich die gleiche Temperatur . Sie sollen sich dann im thermischen Gleichgewicht befinden .

Wie bei der Arbeit hängt die übertragene Wärmemenge vom Pfad ab und nicht nur von den Anfangs- und Endbedingungen des Systems. Es gibt tatsächlich viele Möglichkeiten, das Gas von Zustand i zu Zustand f zu bringen.

Ebenso wie bei der Arbeit ist es wichtig, zwischen Wärme , die einem System von seiner Umgebung zugeführt wird, und Wärme, die von einem System an seine Umgebung abgegeben wird, zu unterscheiden. Q ist positiv für die dem System zugeführte Wärme. Wenn also Wärme das System verlässt, ist Q negativ. Da W in der Gleichung die vom System geleistete Arbeit ist, ist W negativ und E _int nimmt zu , wenn am System gearbeitet wird.

Das Symbol q wird manchmal verwendet, um die Wärme anzuzeigen, die einem System pro Masseneinheit hinzugefügt oder von diesem abgeführt wird . Dies entspricht der Gesamtwärme (Q), die hinzugefügt oder entfernt wird, geteilt durch die Masse (m).

Wärmekapazität

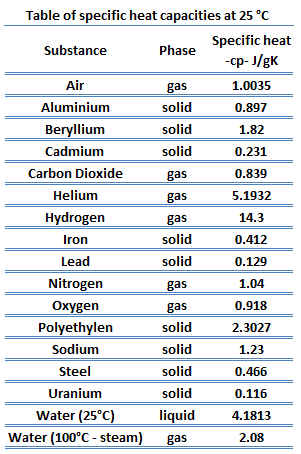Verschiedene Substanzen sind betroffen unterschiedliche Größen durch die Zugabe von Wärme . Wenn verschiedenen Substanzen eine bestimmte Wärmemenge zugesetzt wird, steigen ihre Temperaturen um unterschiedliche Mengen. Diese Proportionalitätskonstante zwischen der Wärme Q , die das Objekt absorbiert oder verliert, und der resultierenden Temperaturänderung T des Objekts ist als Wärmekapazität C eines Objekts bekannt.

C = Q / ΔT

Die Wärmekapazität ist eine umfangreiche Eigenschaft der Materie, dh sie ist proportional zur Größe des Systems. Die Wärmekapazität C hat die Energieeinheit pro Grad oder Energie pro Kelvin. Wenn das gleiche Phänomen wie eine intensive Eigenschaft ausgedrückt wird , wird die Wärmekapazität durch die Menge an Substanz, Masse oder Volumen geteilt, sodass die Menge unabhängig von der Größe oder dem Ausmaß der Probe ist.

Spezifische Wärmekapazität

Die Wärmekapazität eines Stoffes pro Masseneinheit wird als spezifische Wärmekapazität (c _p ) des Stoffes bezeichnet. Der Index p gibt an, dass die Wärmekapazität und die spezifische Wärmekapazität gelten, wenn die Wärme bei konstantem Druck hinzugefügt oder abgeführt wird .

c _p = Q / m & Dgr; T.

Spezifische Wärmekapazität des idealen Gases

Im Idealgasmodell werden die intensiven Eigenschaften c _v und c _p für reine, einfache kompressible Substanzen als partielle Ableitungen der inneren Energie u (T, v) bzw. der Enthalpie h (T, p) definiert :

wobei die Indizes v und p die Variablen bezeichnen, die während der Differenzierung festgehalten werden. Die Eigenschaften c _v und c _p werden als spezifische Wärme (oder Wärmekapazität ) bezeichnet, da sie unter bestimmten besonderen Bedingungen die Temperaturänderung eines Systems mit der durch Wärmeübertragung hinzugefügten Energiemenge in Beziehung setzen. Ihre SI – Einheiten sind J / kg K oder J / mol K . Für Gase sind zwei spezifische Wärmemengen definiert, eine für konstantes Volumen (c _v ) und eine für konstanten Druck (c _p ) .

Nach dem ersten Hauptsatz der Thermodynamik beträgt für einen Prozess mit konstantem Volumen mit einem einatomigen idealen Gas die molare spezifische Wärme:

C _v = 3 / 2R = 12,5 J / mol K.

da

U = 3 / 2nRT

Es kann abgeleitet werden, dass die molare spezifische Wärme bei konstantem Druck ist:

C _p = C _v + R = 5 / 2R = 20,8 J / mol K.

Dieses C _p ist größer als die molare spezifische Wärme bei konstantem Volumen C _v , da nun nicht nur Energie zugeführt werden muss , um die Temperatur des Gases zu erhöhen, sondern auch, damit das Gas funktioniert, da sich in diesem Fall das Volumen ändert.

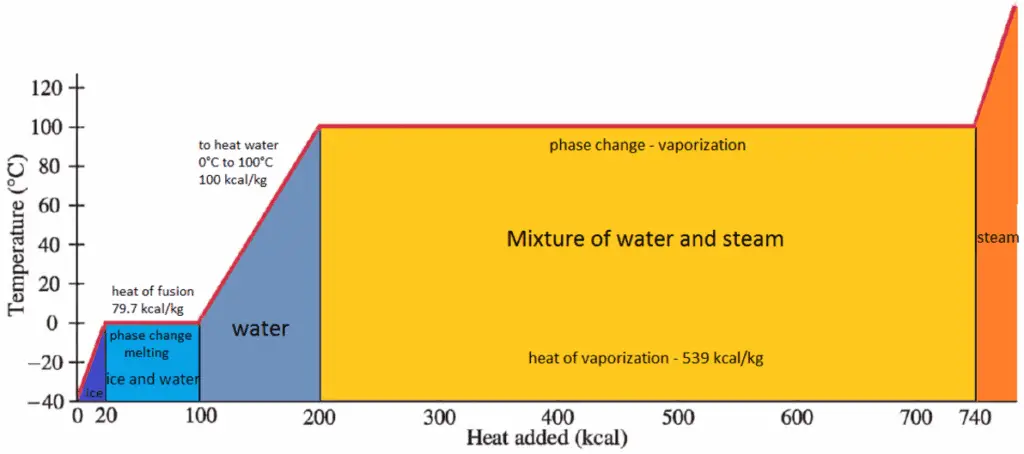
Latente Verdampfungswärme

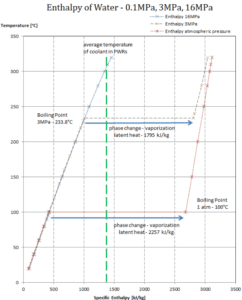
Wenn ein Material die Phase von fest zu flüssig oder von flüssig zu gasförmig ändert, ist im Allgemeinen eine bestimmte Energiemenge an dieser Phasenänderung beteiligt. Im Falle eines Phasenwechsels von Flüssigkeit zu Gas wird diese Energiemenge als Verdampfungsenthalpie (Symbol ∆H _vap ; Einheit: J) bezeichnet, die auch als (latente) Verdampfungswärme oder Verdampfungswärme bezeichnet wird. Latente Wärme ist die Wärmemenge, die einer Substanz hinzugefügt oder von ihr entfernt wird, um eine Phasenänderung zu erzeugen. Diese Energie baut die intermolekularen Anziehungskräfte auf und muss auch die Energie liefern, die zur Expansion des Gases erforderlich ist (die pΔV-Arbeit). Wenn latente Wärme hinzugefügt wird, tritt keine Temperaturänderung auf. Die Verdampfungsenthalpie ist eine Funktion des Drucks, bei dem diese Umwandlung stattfindet.

Latente Verdampfungswärme – Wasser mit 0,1 MPa (atmosphärischer Druck)

h _lg = 2257 kJ / kg

Latente Verdampfungswärme – Wasser mit 3 MPa (Druck in einem Dampferzeuger)

h _lg = 1795 kJ / kg

Verdampfungswärme – Wasser bei 16 MPa (Druck in einem Druckhalter )

h _lg = 931 kJ / kg

Die Verdampfungswärme nimmt mit zunehmendem Druck ab, während der Siedepunkt steigt. Es verschwindet vollständig an einem bestimmten Punkt, der als kritischer Punkt bezeichnet wird . Oberhalb des kritischen Punktes sind die flüssige und die dampfförmige Phase nicht zu unterscheiden, und die Substanz wird als überkritische Flüssigkeit bezeichnet .

Die Verdampfungswärme ist die Wärme, die erforderlich ist, um eine Einheit gesättigter Flüssigkeit vollständig zu verdampfen (oder eine Einheit Masse gesättigten Dampfes zu kondensieren) und gleich h _lg = h _g – h _l .

Die Wärme, die erforderlich ist, um eine Masseeinheit an der Substanz bei konstantem Druck zu schmelzen (oder einzufrieren), ist die Schmelzwärme und ist gleich h _sl = h _l – h _s , wobei h _s die Enthalpie von gesättigtem Feststoff und h _{l ist} ist die Enthalpie der gesättigten Flüssigkeit.

Arbeit in der Thermodynamik

In der Thermodynamik ist die Arbeit eines Systems die Energie, die das System an seine Umgebung überträgt. Kinetische Energie, potentielle Energie und innere Energie sind Energieformen, die Eigenschaften eines Systems sind. Arbeit ist eine Form von Energie , aber es ist Energie auf der Durchreise . Ein System enthält keine Arbeit, Arbeit ist ein Prozess, der von oder auf einem System ausgeführt wird. Im Allgemeinen wird Arbeit für mechanische Systeme als die Wirkung einer Kraft auf ein Objekt über eine Distanz definiert.

W = F. d

wo:

W = Arbeit (J)

F = Kraft (N)

d = Verschiebung (m)

pΔV Arbeit

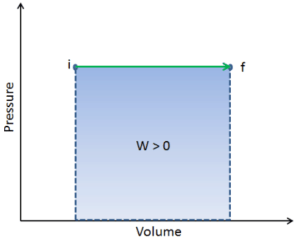
Druck-Volumen-Arbeit (oder pΔV- Arbeit ) tritt auf, wenn sich das Volumen V eines Systems ändert. Die pΔV- Arbeit ist gleich der Fläche unter der Prozesskurve, die im Druck-Volumen-Diagramm aufgetragen ist. Es ist auch als Grenzarbeit bekannt . Grenzarbeit  tritt auf, weil die Masse der Substanz, die in der Systemgrenze enthalten ist, bewirkt, dass eine Kraft, der Druck mal die Oberfläche, auf die Grenzfläche einwirkt und sie bewegt. Grenzarbeit  (oder  pΔV- Arbeit ) tritt auf, wenn sich das  Volumen V eines Systems ändert . Es wird zur Berechnung der Kolbenverdrängungsarbeit in einem  geschlossenen System verwendet    . Dies ist der Fall, wenn sich  Dampf oder Gas in einer Kolben-Zylinder-Vorrichtung gegen den Kolben ausdehnt und den Kolben zur Bewegung zwingt.

Beispiel:

Stellen Sie sich einen reibungslosen Kolben vor, der verwendet wird, um einen konstanten Druck von 500 kPa in einem Zylinder bereitzustellen , der Dampf ( überhitzten Dampf ) mit einem Volumen von 2 m ³  bei 500 K enthält .

Berechnen der Endtemperatur, falls 3000 kJ von Wärme hinzugefügt wird.

Lösung:

Anhand von Dampftabellen wissen wir, dass die spezifische Enthalpie eines solchen Dampfes (500 kPa; 500 K) etwa 2912 kJ / kg beträgt . Da der Dampf unter diesen Bedingungen eine Dichte von 2,2 kg / m ^{3 hat} , wissen wir, dass sich bei einer Enthalpie von 2912 kJ / kg x 4,4 kg = 12812 kJ etwa 4,4 kg Dampf im Kolben befinden .

Wenn wir einfach Q = H ₂ – H _{1 verwenden} , ist die resultierende Dampfenthalpie:

H ₂ = H ₁ + Q = 15812 kJ

Von Dampftabellen , wie Heißdampf (15812 / 4,4 = 3593 kJ / kg) wird eine Temperatur von haben 828 K (555 ° C) . Da der Dampf bei dieser Enthalpie eine Dichte von 1,31 kg / m ^{3 hat} , ist es offensichtlich, dass er sich um etwa 2,2 / 1,31 = 1,67 (+ 67%) ausgedehnt hat. Daher beträgt das resultierende Volumen 2 m ³ × 1,67 = 3,34 m ³ und ∆V = 3,34 m ³ – 2 m ³ = 1,34 m ³ .

Der p∆V- Teil der Enthalpie, dh die geleistete Arbeit, ist:

W = p∆V = 500 000 Pa × 1,34 m ³ = 670 kJ

———–

Während der Volumenänderung , der Druck und Temperatur können auch geändert werden . Um solche Prozesse zu berechnen, müssten wir wissen, wie sich der Druck mit dem Volumen für den tatsächlichen Prozess ändert, durch den sich das System von Zustand i zu Zustand f ändert . Der erste Hauptsatz der Thermodynamik und der Arbeit kann dann ausgedrückt werden als:

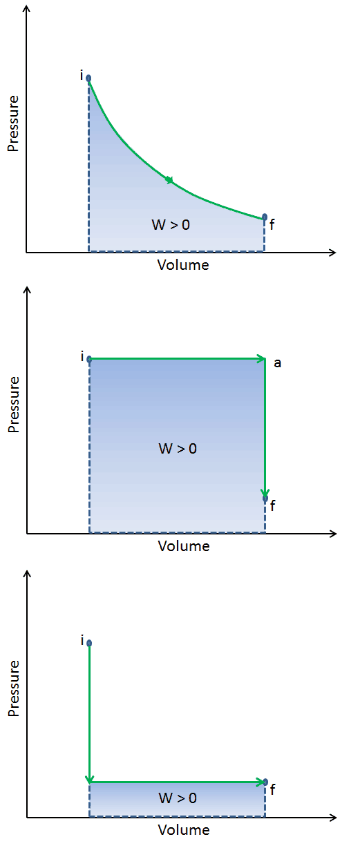
Wenn ein thermodynamisches System von einem Anfangszustand in einen Endzustand wechselt, durchläuft es eine Reihe von Zwischenzuständen . Wir nennen diese Reihe von Zuständen einen Weg . Für diese Zwischenzustände gibt es immer unendlich viele verschiedene Möglichkeiten. Wenn sie alle Gleichgewichtszustände sind, kann der Pfad in einem pV-Diagramm aufgezeichnet werden . Eine der wichtigsten Schlussfolgerungen ist:

Die vom System geleistete Arbeit hängt nicht nur von den Anfangs- und Endzuständen ab, sondern auch von den Zwischenzuständen, dh vom Pfad.

Q und W sind pfadabhängig, während ΔE _int pfadunabhängig ist. Wie aus dem Bild (pV-Diagramm) ersichtlich, ist die Arbeit eine pfadabhängige Variable. Der blaue Bereich stellt die pΔV- Arbeit dar , die von einem System ausgeführt wird, wenn es von einem Anfangszustand i in einen Endzustand f übergeht. Arbeit W ist positiv, weil das Systemvolumen zunimmt. Der zweite Prozess zeigt, dass die Arbeit größer ist und vom Pfad des Prozesses abhängt.

Darüber hinaus können wir das System durch eine Reihe von Zuständen führen, die eine geschlossene Schleife bilden , wie z. B. i ⇒ f ⇒ i . In diesem Fall ist der Endzustand derselbe wie der Anfangszustand , aber die vom System geleistete Gesamtarbeit ist nicht Null . Ein positiver Wert für die Arbeit zeigt an, dass das System an seiner Umgebung arbeitet. Ein negativer Wert zeigt an, dass die Umgebung am System arbeitet.

Beispiel: Turbinenspezifische Arbeit

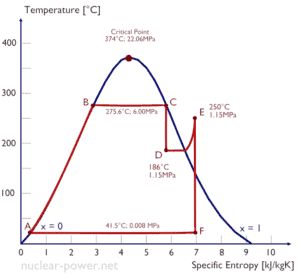
Eine Hochdruckstufe der Dampfturbine arbeitet im stationären Zustand mit Einlassbedingungen von   6 MPa , t = 275,6 ° C , x = 1 (Punkt C). Dampf verlässt diese Turbinenstufe mit einem Druck von 1,15 MPa , 186 ° C und x = 0,87 (Punkt D). Berechnen Sie die Enthalpiedifferenz zwischen diesen beiden Zuständen. Bestimmen Sie die spezifische Arbeitsübertragung.

Die Enthalpie für den Zustand C kann direkt aus Dampftabellen entnommen werden , während die Enthalpie für den Zustand D anhand der Dampfqualität berechnet werden muss :

h _{1, nass} = 2785 kJ / kg

h _{2, nass} = h _{2, s} x + (1 – x) h _{2, l}  = 2782. 0,87 + (1 – 0,87). 790 = 2420 + 103 = 2523 kJ / kg

Δh = 262 kJ / kg

Da im adiabatischen Prozess dh = dw ist , ist Δh = 262 kJ / kg die turbinenspezifische Arbeit .

Vier Sonderfälle des ersten Hauptsatzes der Thermodynamik

Der erste Hauptsatz der Thermodynamik findet in mehreren Sonderfällen Anwendung:

Adiabatischer Prozess:

Ein adiabatischer Prozess ist ein Prozess, bei dem keine Wärmeübertragung in das System oder aus dem System erfolgt. Es tritt sehr schnell auf oder ein System ist gut isoliert, so dass keine Energieübertragung als Wärme zwischen dem System und seiner Umgebung stattfindet. Daher ist dQ = 0 im ersten Hauptsatz der Thermodynamik, der dann lautet:

dQ = 0, dE _int = – dW

Isochorischer Prozess:

Ein isochorischer Prozess ist ein Prozess, bei dem sich das Volumen nicht ändert . Ein isochorer Prozess ist ein Prozess mit konstantem Volumen. Wenn das Volumen eines thermodynamischen Systems konstant ist, arbeitet es nicht an seiner Umgebung. Daher ist dW = 0 im ersten Hauptsatz der Thermodynamik, der dann lautet:

dW = 0, dE _int = dQ

In einem isochoren Prozess verbleibt die gesamte als Wärme hinzugefügte Energie ( dh Q ist positiv) als Erhöhung der inneren Energie ( Erhöhung der Temperatur ) im System .

Zyklischer Prozess:

Ein Prozess, der ein System schließlich in seinen Ausgangszustand zurückversetzt, wird als zyklischer Prozess bezeichnet . Am Ende eines Zyklus haben alle Eigenschaften den gleichen Wert wie zu Beginn.

Für einen solchen Prozess ist der Endzustand derselbe wie der Anfangszustand, und daher muss die gesamte interne Energieänderung Null sein . Dampf (Wasser), der durch einen geschlossenen Kühlkreislauf zirkuliert, durchläuft einen Kreislauf. Der erste Hauptsatz der Thermodynamik lautet dann:

dE _int = 0, dQ = dW

Daher muss das während des Prozesses geleistete Netz genau der Nettowarenmenge entsprechen, die als Wärme übertragen wird.

Kostenlose Erweiterung:

Dies ist ein  adiabatischer Prozess, bei dem keine Wärmeübertragung zwischen dem System und seiner Umgebung stattfindet und keine Arbeiten am oder vom System ausgeführt werden. Diese Arten von adiabatischen Prozessen werden als freie Expansion bezeichnet . Es ist ein irreversibler Prozess, bei dem sich ein Gas in eine isolierte evakuierte Kammer ausdehnt. Es wird auch Joule-Erweiterung genannt . Für ein ideales Gas ändert sich die Temperatur nicht (siehe: Joules zweites Gesetz ), jedoch erfahren echte Gase während der freien Expansion eine Temperaturänderung. Bei der freien Expansion ist Q = W = 0, und das erste Gesetz verlangt Folgendes:

dE _int = 0

Eine freie Expansion kann nicht in einem PV-Diagramm dargestellt werden, da der Prozess schnell und nicht quasistatisch ist. Die Zwischenzustände sind keine Gleichgewichtszustände, und daher ist der Druck nicht klar definiert.