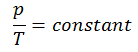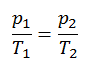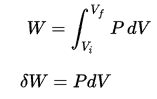Isochorischer Prozess – Isometrischer Prozess
Ein isochorer Prozess ist ein thermodynamischer Prozess, bei dem das Volumen des geschlossenen Systems konstant bleibt (V = const). Es beschreibt das Verhalten von Gas im Behälter, das nicht verformt werden kann. Da das Volumen konstant bleibt, funktioniert der Wärmeübergang in oder aus dem System nicht mit dem p∆V , sondern ändert nur die innere Energie (die Temperatur) des Systems.
Für ein ideales Gas und einen polytropischen Prozess entspricht der Fall n ➝ ∞ einem isochoren Prozess (mit konstantem Volumen) . Im Gegensatz zum adiabatischen Prozess , bei dem n = und ein System keine Wärme mit seiner Umgebung austauscht (Q = 0; W ≠ 0 ) , ändert sich bei einem isochoren Prozess die innere Energie (aufgrund von ∆T ≠ 0) und daher ΔU ≠ 0 (für ideale Gase) und (Q ≠ 0; W = 0 ).
In der Konstruktion von Verbrennungsmotoren sind isochore Prozesse für ihre thermodynamischen Kreisprozessen (Otto- und Dieselzyklus) sehr wichtig, daher ist die Untersuchung dieses Prozesses für die Automobiltechnik von entscheidender Bedeutung.
Isochorischer Prozess und das erste Gesetz
Die klassische Form des ersten Hauptsatzes der Thermodynamik ist die folgende Gleichung:
dU = dQ – dW
In dieser Gleichung ist dW gleich dW = pdV und ist bekannt als die Grenz Arbeit . Dann:
dU = dQ – pdV
Beim isochoren Prozess und beim idealen Gas wird die gesamte dem System zugeführte Wärme zur Erhöhung der inneren Energie verwendet.
Isochorischer Prozess (pdV = 0):
dU = dQ (für ideales Gas)
Isochorischer Prozess – Ideale Gasgleichung
Siehe auch: Was ist ein ideales Gas?
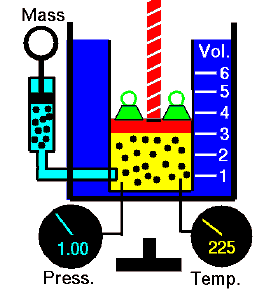
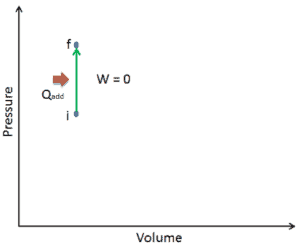Nehmen wir eine isochore Wärmezufuhr in einem idealen Gas an. In einem idealen Gas haben Moleküle kein Volumen und interagieren nicht. Nach dem idealen Gasgesetz ändert sich der Druck linear mit Temperatur und Menge und umgekehrt mit dem Volumen .
pV = nRT
wo:
- p ist der absolute Druck des Gases
- n ist die Substanzmenge
- T ist die absolute Temperatur
- V ist die Lautstärke
- R ist die ideale oder universelle Gaskonstante, die dem Produkt der Boltzmann-Konstante und der Avogadro-Konstante entspricht.
In dieser Gleichung ist das Symbol R eine Konstante, die als universelle Gaskonstante bezeichnet wird und für alle Gase den gleichen Wert hat, nämlich R = 8,31 J / mol K.
Der isochore Prozess kann mit dem idealen Gasgesetz ausgedrückt werden als:
oder
In einem pV-Diagramm erfolgt der Prozess entlang einer horizontalen Linie mit der Gleichung V = konstant.
Druck-Volumen-Arbeit durch das geschlossene System ist definiert als:
Da der Prozess isochor ist , dV = 0 , ist die Druck-Volumen-Arbeit gleich Null . Nach dem idealen Gasmodell kann die innere Energie berechnet werden durch:
∆U = mc v ∆T
wobei die Eigenschaft c v (J / mol K) als spezifische Wärme (oder Wärmekapazität ) bei konstantem Volumen bezeichnet wird, weil sie unter bestimmten besonderen Bedingungen (konstantes Volumen) die Temperaturänderung eines Systems mit der durch zugesetzten Energiemenge in Beziehung setzt Wärmeübertragung.
Da das oder das System keine Arbeit leistet, schreibt der erste Hauptsatz der Thermodynamik ∆U = ∆Q vor. Deshalb:
Q = mc v ∆T
Siehe auch: Spezifische Wärme bei konstantem Volumen und konstantem Druck
Siehe auch: Mayer-Formel
Guy-Lussacs Gesetz
Das Guy-Lussac-Gesetz oder das Druckgesetz, eines der Gasgesetze, besagt:
Bei einer festen Gasmasse bei konstantem Volumen ist der Druck direkt proportional zur Kelvin-Temperatur.
Das heißt, wenn Sie beispielsweise die Temperatur verdoppeln, verdoppeln Sie den Druck. Wenn Sie die Temperatur halbieren, halbieren Sie den Druck.
Sie können dies mathematisch ausdrücken als:
p = konstant. T.
Ja, es scheint identisch zu sein mit dem isochoren Prozess des idealen Gases. Diese Ergebnisse stimmen voll und ganz mit dem idealen Gasgesetz überein, das bestimmt, dass die Konstante gleich nR / V ist. Wenn Sie die pV = nRT-Gleichung neu ordnen, indem Sie beide Seiten durch V teilen, erhalten Sie:
p = nR / V. T.
wobei nR / V konstant ist und:
- p ist der absolute Druck des Gases
- n ist die Substanzmenge
- T ist die absolute Temperatur
- V ist die Lautstärke
- R ist die ideale oder universelle Gaskonstante, die dem Produkt der Boltzmann-Konstante und der Avogadro-Konstante entspricht
Beispiel eines isochoren Prozesses – Isochore Wärmezugabe
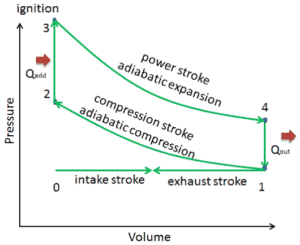Nehmen wir den Otto-Zyklus an , der einer der häufigsten thermodynamischen Kreisprozessen ist, die in Automotoren zu finden sind . Dieser Zyklus setzt voraus, dass die Wärmezufuhr sofort erfolgt ( zwischen 2 → 3 ), während sich der Kolben im oberen Totpunkt befindet. Dieser Prozess wird als isochor angesehen.
Die Prozesse 2 → 3 und 4 → 1 sind isochore Prozesse , bei denen die Wärme zwischen 2 → 3 und zwischen 4 → 1 aus dem System in das System übertragen wird. Während dieser Prozesse werden keine Arbeiten am System durchgeführt oder dem System entzogen . Der isochore Prozess 2 → 3 soll die Zündung des Kraftstoff-Luft-Gemisches und die anschließende schnelle Verbrennung darstellen.
……………………………………………………………………………………………………………………………….
Dieser Artikel basiert auf der maschinellen Übersetzung des englischen Originalartikels. Weitere Informationen finden Sie im Artikel auf Englisch. Sie können uns helfen. Wenn Sie die Übersetzung korrigieren möchten, senden Sie diese bitte an: translations@nuclear-power.com oder füllen Sie das Online-Übersetzungsformular aus. Wir bedanken uns für Ihre Hilfe und werden die Übersetzung so schnell wie möglich aktualisieren. Danke.
