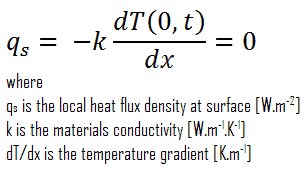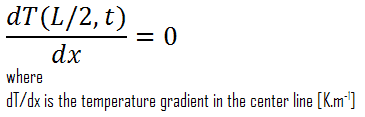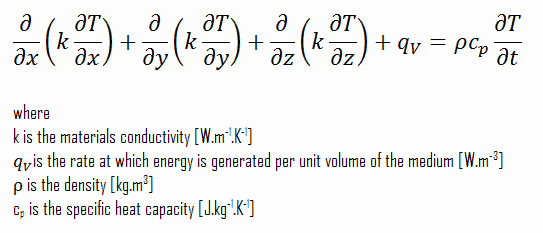Neumann-Randbedingung – Typ II-Randbedingung
In der Mathematik ist die Neumann-Randbedingung eine Randbedingung, die nach dem deutschen Mathematiker Carl Neumann (1832–1925) benannt wurde. Wenn es einer gewöhnlichen oder partiellen Differentialgleichung auferlegt wird, gibt es die Werte an, die eine Lösung entlang der Domänengrenze annehmen muss.
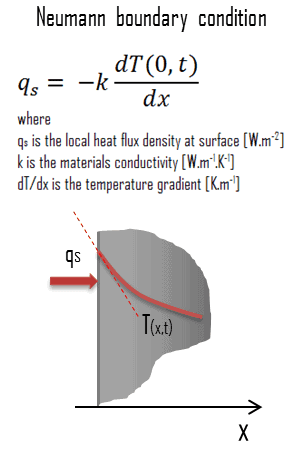
Bei Wärmeübertragungsproblemen entspricht die Neumann-Bedingung einer vorgegebenen Temperaturänderungsrate . Mit anderen Worten, dieser Zustand setzt voraus, dass der Wärmefluss an der Oberfläche des Materials bekannt ist. Der Wärmefluss in positiver x-Richtung an einer beliebigen Stelle im Medium, einschließlich der Grenzen, kann durch das Fourier-Gesetz der Wärmeleitung ausgedrückt werden .
Sonderfall – Adiabatische Grenze – Perfekt isolierte Grenze
Ein Sonderfall dieser Bedingung entspricht der perfekt isolierten Oberfläche, für die (∂T / ∂x = 0). Die Wärmeübertragung durch eine ordnungsgemäß isolierte Oberfläche kann als Null angenommen werden, da eine angemessene Isolierung die Wärmeübertragung durch eine Oberfläche auf ein vernachlässigbares Maß reduziert. Mathematisch kann diese Randbedingung ausgedrückt werden als:
Sonderfall – Thermische Symmetrie
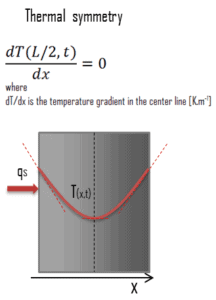Ein weiterer sehr wichtiger Fall, der zur Lösung von Wärmeübertragungsproblemen mit Brennstäben verwendet werden kann, ist die thermische Symmetrie. Zum Beispiel werden die zwei Oberflächen einer großen Heizplatte der Dicke L, die vertikal an der Luft aufgehängt ist, den gleichen thermischen Bedingungen ausgesetzt, und somit ist die Temperaturverteilung symmetrisch (dh in einer Hälfte der Platte ist das gleiche Temperaturprofil wie das in der anderen Hälfte). Infolgedessen muss sich in der Mittellinie der Platte ein Maximum befinden, und die Mittellinie kann als isolierte Oberfläche angesehen werden (∂T / ∂x = 0). Der Wärmezustand auf dieser Symmetrieebene kann ausgedrückt werden als:
Allgemeine Wärmeleitungsgleichung
Die Wärmeleitungsgleichung ist eine partielle Differentialgleichung, die die Verteilung der Wärme (oder des Temperaturfeldes ) in einem bestimmten Körper über die Zeit beschreibt. Detaillierte Kenntnisse des Temperaturfeldes sind für die Wärmeleitung durch Materialien sehr wichtig. Sobald diese Temperaturverteilung bekannt ist, kann der Wärmeleitungsfluss an jedem Punkt im Material oder auf seiner Oberfläche nach dem Fourier-Gesetz berechnet werden .
Die Wärmegleichung leitet sich aus dem Fourier-Gesetz und der Energieerhaltung ab . Das Fourier-Gesetz besagt, dass die zeitliche Wärmeübertragungsrate durch ein Material proportional zum negativen Temperaturgradienten und zu der Fläche im rechten Winkel zu dem Gradienten ist, durch den die Wärme fließt.
Eine Änderung der inneren Energie pro Volumeneinheit im Material ΔQ ist proportional zur Änderung der Temperatur Δu. Das ist:
∆Q = ρ.c p .∆T
Generelle Form
Unter Verwendung dieser beiden Gleichungen können wir die allgemeine Wärmeleitungsgleichung ableiten:
Diese Gleichung wird auch als Fourier-Biot-Gleichung bezeichnet und bietet das grundlegende Werkzeug für die Wärmeleitungsanalyse. Aus seiner Lösung können wir das Temperaturfeld als Funktion der Zeit erhalten.
In Worten heißt es in der Wärmeleitungsgleichung :
Zu jedem Zeitpunkt im Medium muss die Nettorate der Energieübertragung durch Leitung in ein Volumeneinheit plus die Volumenrate der Wärmeenergieerzeugung gleich der Änderungsrate der im Volumen gespeicherten Wärmeenergie sein.
……………………………………………………………………………………………………………………………….
Dieser Artikel basiert auf der maschinellen Übersetzung des englischen Originalartikels. Weitere Informationen finden Sie im Artikel auf Englisch. Sie können uns helfen. Wenn Sie die Übersetzung korrigieren möchten, senden Sie diese bitte an: translations@nuclear-power.com oder füllen Sie das Online-Übersetzungsformular aus. Wir bedanken uns für Ihre Hilfe und werden die Übersetzung so schnell wie möglich aktualisieren. Danke.
