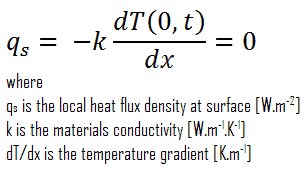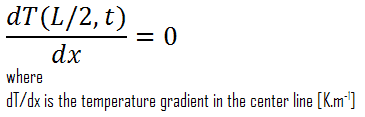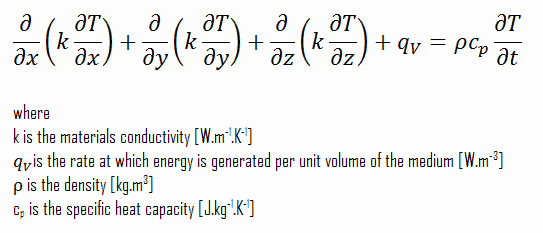Qu’est-ce qu’une condition aux limites de Neumann – Conditions aux limites de type II – Définition

Condition de limite de Neumann – Condition de limite de type II

En mathématiques, la condition limite de Neumann (ou du second type) est un type de condition limite, du nom du mathématicien allemand Carl Neumann (1832-1925). Lorsqu’elle est imposée à une équation différentielle ordinaire ou partielle, elle spécifie les valeurs qu’une solution doit prendre le long des limites du domaine.

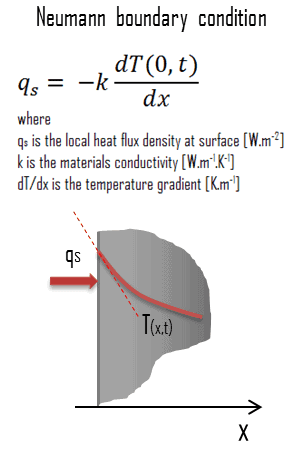
Dans les problèmes de transfert de chaleur, la condition de Neumann correspond à un taux de variation de température donné . En d’autres termes, cette condition suppose que le flux de chaleur à la surface du matériau est connu. Le flux de chaleur dans la direction x positive, n’importe où dans le milieu, y compris les limites, peut être exprimé par la loi de Fourier de la chaleur .

Cas spécial – Limite adiabatique – Limite parfaitement isolée

Un cas particulier de cette condition correspond à la surface parfaitement isolée pour laquelle (T / ∂x = 0). Le transfert de chaleur à travers une surface correctement isolée peut être considéré comme nul, car une isolation adéquate réduit le transfert de chaleur à travers une surface à des niveaux négligeables. Mathématiquement, cette condition limite peut être exprimée comme suit:

Cas spécial – Symétrie thermique

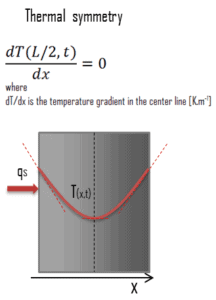Un autre cas très important, qui peut être utilisé pour résoudre des problèmes de transfert de chaleur impliquant des barres de combustible, est la symétrie thermique. Par exemple, les deux surfaces d’une grande plaque chauffante d’épaisseur L suspendue verticalement dans l’air seront soumises aux mêmes conditions thermiques; la répartition de la température sera donc symétrique (c’est-à-dire que, dans une moitié de la plaque, le profil de température sera le même. que dans l’autre moitié). En conséquence, il doit y avoir un maximum dedans dans la ligne centrale de la plaque et la ligne centrale peut être vue comme une surface isolée (∂T / x = 0). La condition thermique à ce plan de symétrie peut être exprimée comme suit:

Équation générale de conduction thermique

L’ équation de conduction thermique est une équation différentielle partielle qui décrit la répartition de la chaleur (ou du champ de température ) dans un corps donné dans le temps. Une connaissance détaillée du champ de température est très importante dans la conduction thermique à travers les matériaux. Une fois cette distribution de température connue, le flux thermique de conduction en un point quelconque du matériau ou à sa surface peut être calculé à partir de la loi de Fourier .

L’équation de la chaleur est dérivée de la loi de Fourier et de la conservation de l’énergie . La loi de Fourier stipule que le taux de transfert de chaleur à travers un matériau est proportionnel au gradient négatif de la température et de la zone, perpendiculairement à ce gradient, à travers lequel la chaleur circule.

Un changement d’énergie interne par unité de volume dans le matériau, ΔQ, est proportionnel au changement de température, Δu. C’est:

∆Q = ρ.c _p .∆T

Forme générale

En utilisant ces deux équations, nous pouvons dériver l’équation générale de conduction thermique:

Cette équation est également connue sous le nom d’ équation de Fourier-Biot et fournit l’outil de base pour l’analyse de conduction thermique. A partir de sa solution, on peut obtenir le champ de température en fonction du temps.

En d’autres termes, l’ équation de conduction thermique indique que:

En tout point du milieu, le taux net de transfert d’énergie par conduction dans un volume unitaire plus le taux volumétrique de génération d’énergie thermique doit être égal au taux de variation de l’énergie thermique stockée dans le volume.