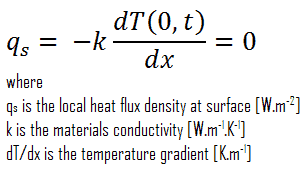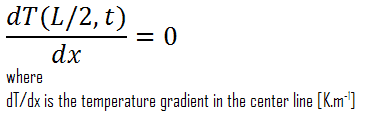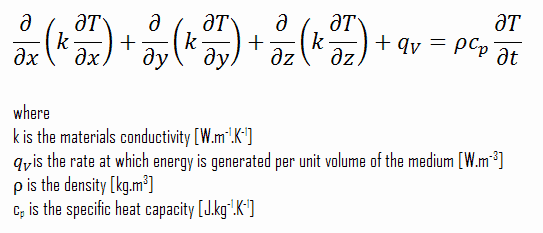What is Neumann Boundary Condition – Type II Boundary Condition – Definition

Neumann Boundary Condition – Type II Boundary Condition

In mathematics, the Neumann (or second-type) boundary condition is a type of boundary condition, named after a German mathematician Carl Neumann (1832–1925). When imposed on an ordinary or a partial differential equation, it specifies the values that a solution needs to take on along the boundary of the domain.

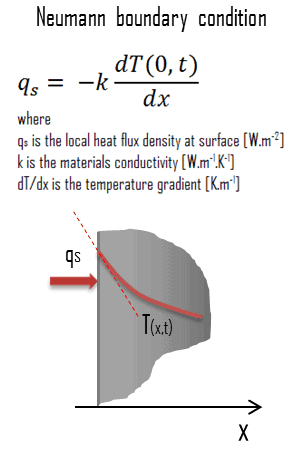
In heat transfer problems, the Neumann condition corresponds to a given rate of change of temperature. In other words, this condition assumes that the heat flux at the surface of the material is known. The heat flux in the positive x-direction anywhere in the medium, including the boundaries, can be expressed by Fourier’s law of heat conduction.

Special Case – Adiabatic Boundary – Perfectly Insulated Boundary

A special case of this condition corresponds to the perfectly insulated surface for which (∂T/∂x = 0). Heat transfer through a properly insulated surface can be taken to be zero since adequate insulation reduces heat transfer through a surface to negligible levels. Mathematically, this boundary condition can be expressed as:

Special Case – Thermal Symmetry

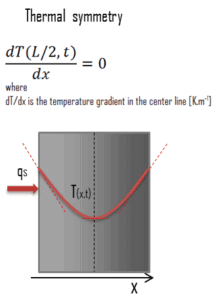Another very important case, that can be used for solving heat transfer problems involving fuel rods, is the thermal symmetry. For example, the two surfaces of a large hot plate of thickness L suspended vertically in air will be subjected to the same thermal conditions, and thus the temperature distribution will be symmetrical (i.e. in one half of the plate will be the same temperature profile as that in the other half). As a result, there must be a maximum in in the center line of the plate and the center line can be viewed as an insulated surface (∂T/∂x = 0). The thermal condition at this plane of symmetry can be expressed as:

General Heat Conduction Equation

The heat conduction equation is a partial differential equation that describes the distribution of heat (or the temperature field) in a given body over time. Detailed knowledge of the temperature field is very important in thermal conduction through materials. Once this temperature distribution is known, the conduction heat flux at any point in the material or on its surface may be computed from Fourier’s law.

The heat equation is derived from Fourier’s law and conservation of energy. The Fourier’s law states that the time rate of heat transfer through a material is proportional to the negative gradient in the temperature and to the area, at right angles to that gradient, through which the heat flows.

A change in internal energy per unit volume in the material, ΔQ, is proportional to the change in temperature, Δu. That is:

∆Q = ρ.c_p.∆T

General Form

Using these two equation we can derive the general heat conduction equation:

This equation is also known as the Fourier-Biot equation, and provides the basic tool for heat conduction analysis. From its solution, we can obtain the temperature field as a function of time.

In words, the heat conduction equation states that:

At any point in the medium the net rate of energy transfer by conduction into a unit volume plus the volumetric rate of thermal energy generation must equal the rate of change of thermal energy stored within the volume.

See also:

Heat Equation