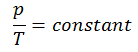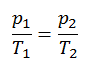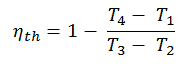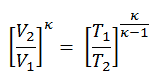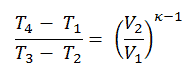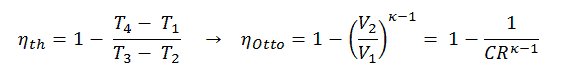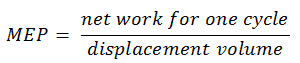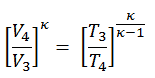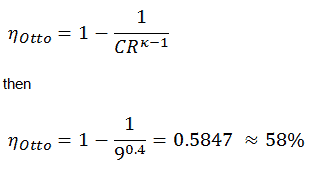Was ist Otto-Kreisprozess – Ottomotor – Definition

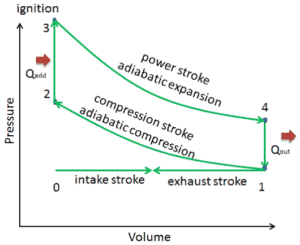
In einem idealen Otto-Zyklus durchläuft das System, das den Zyklus ausführt, eine Reihe von vier intern reversiblen Prozessen: zwei isentrope (reversible adiabatische) Prozesse, die sich mit zwei isochoren Prozessen abwechseln:

1. Isentrope Kompression (Kompressionshub) – Das Gas (Kraftstoff-Luft-Gemisch) wird adiabatisch von Zustand 1 nach Zustand 2 komprimiert, wenn sich der Kolben vom unteren Totpunkt zum oberen Totpunkt bewegt. Die Umgebung arbeitet am Gas, erhöht seine innere Energie (Temperatur) und komprimiert es. Andererseits bleibt die Entropie unverändert. Die Volumenänderungen und das Verhältnis ( V ₁ / V ₂ ) werden als Kompressionsverhältnis bezeichnet.
2. Isochore Kompression (Zündphase) – In dieser Phase (zwischen Zustand 2 und Zustand 3) erfolgt eine Wärmeübertragung mit konstantem Volumen (der Kolben befindet sich in Ruhe) von einer externen Quelle auf die Luft, während sich der Kolben im oberen Totpunkt in Ruhe befindet . Dieser Prozess soll die Zündung des in die Kammer eingespritzten Kraftstoff-Luft-Gemisches und die anschließende schnelle Verbrennung darstellen. Der Druck steigt und das Verhältnis ( P ₃ / P ₂ ) wird als “Explosionsverhältnis” bezeichnet.
3. Isentropische Expansion (Krafthub) – Das Gas expandiert adiabatisch von Zustand 3 zu Zustand 4, wenn sich der Kolben vom oberen Totpunkt zum unteren Totpunkt bewegt. Das Gas wirkt auf die Umgebung (Kolben) und verliert eine Menge an interner Energie, die der Arbeit entspricht, die das System verlässt. Auch hier bleibt die Entropie unverändert. Das Volumenverhältnis ( V ₄ / V ₃ ) ist als isentropisches Expansionsverhältnis bekannt, aber für den Otto-Zyklus ist es gleich dem Kompressionsverhältnis.
4. Isochore Dekompression (Abgashub) – In dieser Phase wird der Zyklus durch einen Prozess mit konstantem Volumen abgeschlossen, bei dem der Luft Wärme entzogen wird, während sich der Kolben im unteren Totpunkt befindet. Der Arbeitsgasdruck fällt augenblicklich von Punkt 4 auf Punkt 1 ab. Das Auslassventil öffnet bei Punkt 4. Der Auslasshub erfolgt unmittelbar nach dieser Dekompression. Wenn sich der Kolben bei geöffnetem Auslassventil vom unteren Totpunkt (Punkt 1) zum oberen Totpunkt (Punkt 0) bewegt, wird das Gasgemisch in die Atmosphäre abgelassen und der Prozess beginnt von neuem.

Während des Otto-Zyklus wird vom Kolben zwischen den Zuständen 1 und 2 ( isentropische Kompression ) am Gas gearbeitet . Die Arbeit am Gas am Kolben erfolgt zwischen den Stufen 3 und 4 ( isentropische Expansion ). Der Unterschied zwischen der vom Gas geleisteten Arbeit und der am Gas geleisteten Arbeit ist das vom Kreislauf erzeugte Netz und entspricht der von der Kreislaufkurve umschlossenen Fläche. Die durch den Zyklus erzeugte Arbeit multipliziert mit der Geschwindigkeit des Zyklus (Zyklen pro Sekunde) entspricht der vom Otto-Motor erzeugten Leistung.

Otto-Zyklus – pV, Ts-Diagramm

Der Otto-Zyklus wird häufig in einem Druck-Volumen-Diagramm ( pV-Diagramm ) und in einem Temperatur-Entropie-Diagramm (Ts-Diagramm) dargestellt. In einem Druckvolumendiagramm folgen die isochoren Prozesse den isochoren Linien für das Gas (die vertikalen Linien). Adiabatische Prozesse bewegen sich zwischen diesen vertikalen Linien und der durch den gesamten Zyklusweg begrenzte Bereich repräsentiert die Gesamtarbeit, die während eines Prozesses ausgeführt werden kann Zyklus.

Das Temperatur-Entropie-Diagramm ( Ts-Diagramm ), in dem der thermodynamische Zustand durch einen Punkt in einem Diagramm mit spezifischen Entropien als horizontale Achse und absoluter Temperatur (T) als vertikaler Achse angegeben wird. Ts-Diagramme sind ein nützliches und allgemeines Werkzeug, insbesondere weil sie dazu beitragen, die Wärmeübertragung während eines Prozesses zu visualisieren. Bei reversiblen (idealen) Prozessen ist die Fläche unter der Ts-Kurve eines Prozesses die Wärme, die während dieses Prozesses auf das System übertragen wird.

Otto Cycle – Viertaktmotor

Der Otto-Zyklus ist eine Reihe von Prozessen, die von Verbrennungsmotoren mit Fremdzündung verwendet werden (Zweitakt- oder Viertakt-Zyklen). Nikolaus August Otto entwarf zunächst den sogenannten Viertaktmotor. Ein Hub bezieht sich auf die volle Bewegung des Kolbens entlang des Zylinders in beide Richtungen. Daher entspricht jeder nicht einem einzelnen thermodynamischen Prozess, der im Kapitel Otto-Zyklus – Prozesse angegeben ist.

Der Viertaktmotor umfasst:

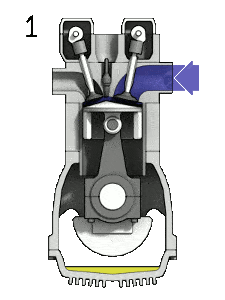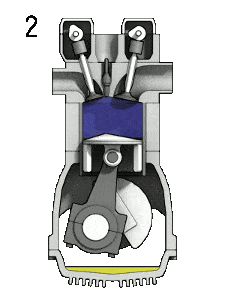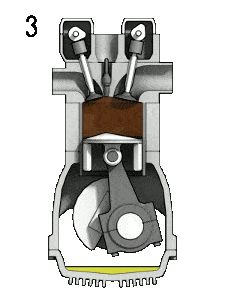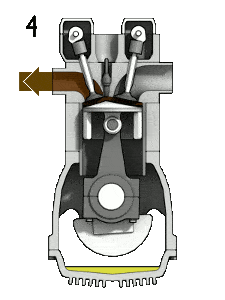
• Einlasshub – Der Kolben bewegt sich vom oberen Totpunkt (OT) zum unteren Totpunkt (OT) und der Zyklus passiert die Punkte 0 → 1. Bei diesem Hub ist das Einlassventil geöffnet, während der Kolben ein Luft-Kraftstoff-Gemisch in den Zylinder zieht durch Erzeugen eines Vakuumdrucks in den Zylinder durch seine Abwärtsbewegung.
• der Kompressionshub – Der Kolben bewegt sich vom unteren Totpunkt (BDC) zum oberen Totpunkt (OT) und der Zyklus passiert die Punkte 1 → 2. Bei diesem Hub sind sowohl das Einlass- als auch das Auslassventil geschlossen, daher wird das Kraftstoff-Luft-Gemisch komprimiert. Am Ende dieses Hubs wird das Kraftstoff-Luft-Gemisch durch einen Funken gezündet, der einen weiteren Druck- und Temperaturanstieg in der Kammer bewirkt. Am Ende dieses Hubs hat die Kurbelwelle eine volle 360-Grad-Umdrehung ausgeführt.
• Krafthub – Der Kolben bewegt sich vom oberen Totpunkt (OT) zum unteren Totpunkt (OT) und der Zyklus passiert die Punkte 2 → 3 → 4. Bei diesem Hub sind sowohl das Einlass- als auch das Auslassventil geschlossen. Zu Beginn des Arbeitstakts entzündet ein Funke das Kraftstoff-Luft-Gemisch in der Brennkammer, was wiederum eine sehr schnelle Verbrennung des Kraftstoffs bewirkt. Bei diesem Hub wird der Kolben in Richtung der Kurbelwelle angetrieben, das Volumen erhöht sich und der Druck fällt ab, wenn das Gas am Kolben arbeitet.
• der Auspuffhub. Der Kolben bewegt sich vom unteren Totpunkt (UT) zum oberen Totpunkt (OT) und der Zyklus passiert die Punkte 4 → 1 → 0. Bei diesem Hub ist das Auslassventil geöffnet, während der Kolben ein Abgas aus der Kammer zieht. Am Ende dieses Hubs hat die Kurbelwelle eine zweite volle 360-Grad-Umdrehung abgeschlossen.

Vergleich von tatsächlichen und idealen Otto-Zyklen

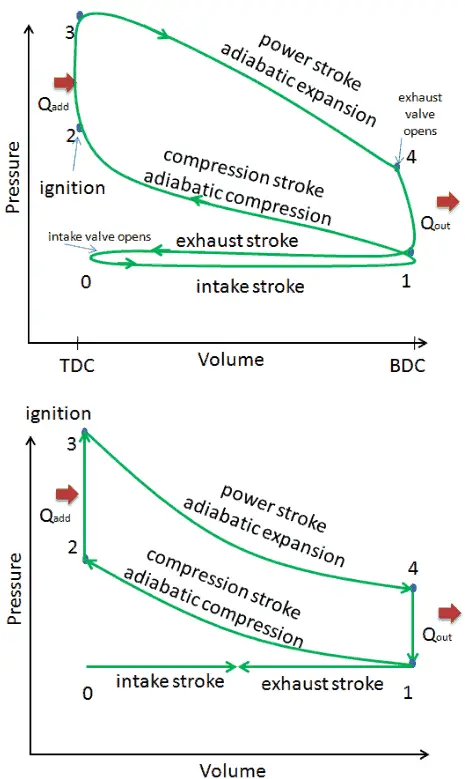In diesem Abschnitt wird ein idealer Otto-Zyklus gezeigt, bei dem viele Annahmen vom tatsächlichen Otto-Zyklus abweichen . Die Hauptunterschiede zwischen dem tatsächlichen und dem idealen Otto-Motor sind in der Abbildung dargestellt. In der Realität tritt der ideale Zyklus nicht auf und mit jedem Prozess sind viele Verluste verbunden. Für einen tatsächlichen Zyklus ähnelt die Form des pV-Diagramms dem Ideal, aber die vom pV-Diagramm eingeschlossene Fläche (Arbeit) ist immer kleiner als der ideale Wert. Der ideale Otto-Zyklus basiert auf folgenden Annahmen:

• Geschlossener Zyklus.  Der größte Unterschied zwischen den beiden Diagrammen besteht in der Vereinfachung der Einlass- und Auslasshübe im idealen Zyklus. Im Auspuffhub wird die Wärme Q _out an die Umgebung abgegeben, bei einem realen Motor verlässt das Gas den Motor und wird durch ein neues Gemisch aus Luft und Kraftstoff ersetzt.
• Sofortige Wärmezufuhr (isochore Wärmezufuhr). Bei realen Motoren erfolgt die Wärmezufuhr nicht sofort, daher liegt der Spitzendruck nicht bei OT, sondern unmittelbar nach OT.
• Keine Wärmeübertragung (adiabatisch)
  • Kompression – Das Gas (Kraftstoff-Luft-Gemisch) wird adiabatisch von Zustand 1 nach Zustand 2 komprimiert. Bei realen Motoren gibt es immer einige Ineffizienzen, die den thermischen Wirkungsgrad verringern.
  • Erweiterung. Das Gas (Kraftstoff-Luft-Gemisch) dehnt sich adiabatisch von Zustand 3 zu Zustand 4 aus.
• Vollständige Verbrennung des Kraftstoff-Luft-Gemisches.
• Keine Pumparbeit . Pumparbeit ist der Unterschied zwischen der Arbeit während des Auslasshubs und der Arbeit während des Einlasshubs. In realen Zyklen besteht ein Druckunterschied zwischen Abgas- und Eingangsdruck.
• Kein Abblasverlust . Der Abblasverlust wird durch das frühe Öffnen der Auslassventile verursacht. Dies führt zu einem Verlust der Arbeitsleistung während des Expansionshubs.
• Kein Blow-by-Verlust . Der Blow-by-Verlust wird durch das Austreten von Druckgasen durch Kolbenringe und andere Spalten verursacht.
• Keine Reibungsverluste .

Diese vereinfachenden Annahmen und Verluste führen dazu, dass der geschlossene Bereich (Arbeit) des pV-Diagramms für einen tatsächlichen Motor erheblich kleiner ist als die Größe des Bereichs (Arbeit), der vom pV-Diagramm des idealen Zyklus eingeschlossen ist. Mit anderen Worten, der ideale Motorzyklus überschätzt das Netz und, wenn die Motoren mit der gleichen Drehzahl laufen, die vom tatsächlichen Motor erzeugte Leistung um etwa 20%.

Kompressionsverhältnis – Otto Motor

Das Verdichtungsverhältnis , CR , ist als das Verhältnis des Volumens im unteren Totpunkt und das Volumen am oberen Totpunkt definiert ist . Es ist ein Schlüsselmerkmal für viele Verbrennungsmotoren. Im folgenden Abschnitt wird gezeigt, dass das Verdichtungsverhältnis den thermischen Wirkungsgrad des verwendeten thermodynamischen Zyklus des Verbrennungsmotors bestimmt. Im Allgemeinen ist ein hohes Verdichtungsverhältnis erwünscht, da dadurch ein Motor einen höheren thermischen Wirkungsgrad erreichen kann.

Nehmen wir zum Beispiel einen Otto-Zyklus mit einem Kompressionsverhältnis von CR = 10: 1 an. Das Volumen der Kammer beträgt vor dem Kompressionshub 500 cm³ = 500 × 10 ^-6 m ³ (0,5 l). Für diesen Motor eines erforderlichen ll Band sind bekannt:

• V ₁ = V ₄ = V _max = 500 × 10 ^–6 m ³ (0,5 l)
• V ₂ = V ₃ = V _min = V _max / CR = 55,56 × 10 ^–6 m ³

Beachten Sie, dass (V _max – V _min ) x Anzahl der Zylinder = Gesamtmotorhubraum.

Beispiele für Kompressionsverhältnisse – Benzin vs. Diesel

• Das Verdichtungsverhältnis in einem benzinbetriebenen Motor ist aufgrund eines möglichen Motorklopfens (Selbstentzündung) normalerweise nicht viel höher als 10: 1 und nicht niedriger als 6: 1 .
• Ein turbogeladener Subaru Impreza WRX hat ein Verdichtungsverhältnis von 8,0: 1 . Im Allgemeinen haben turbogeladene oder aufgeladene Motoren bereits Druckluft am Lufteinlass, daher werden sie normalerweise mit einem niedrigeren Verdichtungsverhältnis gebaut.
• Ein serienmäßiger Honda S2000 Motor (F22C1) hat ein Verdichtungsverhältnis von 11,1: 1 .
• Einige atmosphärische Sportwagenmotoren können ein Verdichtungsverhältnis von bis zu 12,5: 1 haben (z. B. Ferrari 458 Italia).
• 2012 brachte Mazda neue Benzinmotoren unter dem Markennamen SkyActiv mit einem Verdichtungsverhältnis von 14: 1 auf den Markt . Um das Risiko eines Motorklopfens zu verringern, wird das Restgas durch Verwendung von 4-2-1-Motorabgassystemen , Implementierung eines Kolbenhohlraums und Optimierung der Kraftstoffeinspritzung reduziert .
• Die Dieselmotoren haben ein Verdichtungsverhältnis, das normalerweise 14: 1 überschreitet, und Verhältnisse über 22: 1 sind ebenfalls üblich.

Thermische Effizienz für den Otto-Zyklus

Im allgemeinen wird die thermischen Wirkungsgrad , η _th , ein Wärmekraftmaschine ist als das Verhältnis der definierten Arbeits es tut, W , an den Wärmeeingang bei der hohen Temperatur, Q _H .

Der thermische Wirkungsgrad , η _th , stellt den Anteil an Wärme , Q _H , die konvertiert wird , zu arbeiten . Da Energie nach dem ersten Hauptsatz der Thermodynamik eingespart wird und Energie nicht vollständig in Arbeit umgewandelt werden kann , muss der Wärmeeintrag Q _H gleich der geleisteten Arbeit W plus der Wärme sein, die als Abwärme Q _C an die abgegeben werden muss Umgebung. Daher können wir die Formel für den thermischen Wirkungsgrad wie folgt umschreiben:

Die absorbierte Wärme tritt während der Verbrennung des Kraftstoff-Luft-Gemisches auf, wenn der Funke ungefähr bei konstantem Volumen auftritt. Da während eines isochoren Prozesses keine Arbeit von oder am System ausgeführt wird, schreibt der erste Hauptsatz der Thermodynamik ∆U = ∆Q vor. Daher ist die hinzugefügte und abgegebene Wärme gegeben durch:

Q _add = mc _v (T ₃ – T ₂ )

Q _out = mc _v (T ₄ – T ₁ )

Das Ersetzen der Ausdrücke für die Wärme, die hinzugefügt und im Ausdruck für die thermische Effizienz verworfen wird, ergibt:

Wir können den obigen Ausdruck vereinfachen, indem wir die Tatsache verwenden, dass die Prozesse 1 → 2 und von 3 → 4 adiabatisch sind und für einen adiabatischen Prozess die folgende p, V, T-Formel gültig ist:

Es kann abgeleitet werden, dass:

In dieser Gleichung ist das Verhältnis V ₁ / V ₂ als das Kompressionsverhältnis CR bekannt . Wenn wir den Ausdruck für den thermischen Wirkungsgrad unter Verwendung des Kompressionsverhältnisses umschreiben, schließen wir, dass der thermische Wirkungsgrad des Otto-Zyklus nach Luftstandard eine Funktion des Kompressionsverhältnisses und von  κ = c _p / c _{v ist} .

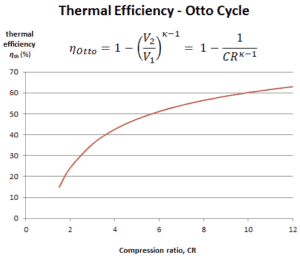
Dies ist eine sehr nützliche Schlussfolgerung, da es wünschenswert ist, ein hohes Kompressionsverhältnis zu erreichen , um mehr mechanische Energie aus einer gegebenen Masse eines Luft-Kraftstoff-Gemisches zu extrahieren. Ein höheres Verdichtungsverhältnis ermöglicht das Erreichen der gleichen Verbrennungstemperatur mit weniger Kraftstoff bei gleichzeitig längerem Expansionszyklus. Dies erzeugt mehr mechanische Leistung und senkt die Abgastemperatur . Das Absenken der Abgastemperatur bewirkt das Absenken der an die Atmosphäre abgegebenen Energie. Diese Beziehung ist in der Abbildung für κ = 1,4 dargestellt, die die Umgebungsluft darstellt.

Selbstentzündung – Grenze für das Kompressionsverhältnis

Bei gewöhnlichen Benzinmotoren hat das Verdichtungsverhältnis seine Grenzen. Das Verdichtungsverhältnis in einem benzinbetriebenen Motor ist aufgrund eines möglichen Motorklopfens ( Selbstentzündung ) normalerweise nicht viel höher als 10: 1 und nicht niedriger als 6: 1 . Höhere Verdichtungsverhältnisse führen jedoch dazu, dass Benzinmotoren einem durch Selbstentzündung verursachten Motorklopfen ausgesetzt werden , wenn Kraftstoff mit niedrigerer Oktanzahl verwendet wird. Das unverbrannte Gemisch kann sich selbst entzünden, indem es allein durch Druck und Hitze detoniert, anstatt sich genau zum richtigen Zeitpunkt von der Zündkerze zu entzünden. Das Klopfen des Motors kann durch Verwendung von Kraftstoff mit hoher Oktanzahl verringert werden, was die Selbstentzündungsbeständigkeit des Benzins erhöht . Je höher die Oktanzahl, desto mehr Kompression kann der Kraftstoff vor der Detonation (Zündung) aushalten. Da die Temperatur, die das Kraftstoff-Luft-Gemisch während der Kompression erreicht, mit zunehmendem Kompressionsverhältnis zunimmt, steigt die Wahrscheinlichkeit einer Selbstentzündung mit dem Kompressionsverhältnis. Die Selbstentzündung kann den Wirkungsgrad verringern oder den Motor beschädigen, wenn keine Klopfsensoren vorhanden sind, um den Zündzeitpunkt zu ändern.

Bei Dieselmotoren (auch als Selbstzündungsmotoren bezeichnet ) können höhere Verdichtungsverhältnisse erreicht werden , da sie den Kraftstoff nicht komprimieren, sondern nur Luft komprimieren und dann Kraftstoff in die durch Kompression erwärmte Luft einspritzen. Kompressionsverhältnisse im Bereich von 12 bis 20 sind typisch für Dieselmotoren. Die größere Expansion bei Dieselmotoren bedeutet, dass sie weniger Wärme in ihren kühleren Abgasen abgeben. Das höhere Verdichtungsverhältnis (größere Ausdehnung) und die höhere Spitzentemperatur führen dazu, dass Dieselmotoren einen höheren thermischen Wirkungsgrad erreichen.

Mittlerer effektiver Druck – MdEP

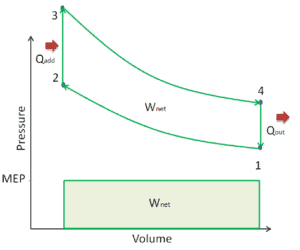
Ein Parameter, der von Ingenieuren zur Beschreibung der Leistung von Hubkolbenmotoren verwendet wird, wird als mittlerer effektiver Druck ( MEP) bezeichnet . MEP ist ein sehr nützliches Maß für die Fähigkeit eines Motors, Arbeiten auszuführen, die unabhängig vom Hubraum des Motors sind. Es gibt verschiedene Arten von Abgeordneten. Diese Abgeordneten werden durch die Standortmessung und die Berechnungsmethode (z. B. BMEP oder IMEP) definiert.

Im Allgemeinen ist der mittlere effektive Druck der theoretische konstante Druck, der, wenn er während des Arbeitshubs auf den Kolben einwirkt, das gleiche Netz erzeugt, das tatsächlich in einem vollständigen Zyklus entwickelt wurde. Der MdEP kann definiert werden als:

Zum Beispiel ist der als IMEP _n bezeichnete mittlere effektive Nettodruck gleich dem mittleren effektiven Druck, der aus dem Zylinderdruck (es muss diese Messung vorhanden sein) über den gesamten Motorzyklus berechnet wird. Beachten Sie, dass es bei einem Viertaktmotor 720 ° und bei einem Zweitaktmotor 360 ° beträgt.

Einige Beispiele:

• Der MEP eines atmosphärischen Benzinmotors kann im Bereich des maximalen Drehmoments zwischen 8 und 11 bar liegen.
• Der MEP eines turbogeladenen Benzinmotors kann zwischen 12 und 17 bar liegen.
• Der MEP eines atmosphärischen Dieselmotors kann zwischen 7 und 9 bar liegen.
• Der MEP eines Dieselmotors mit Turbolader kann zwischen 14 und 18 bar liegen

Beispielsweise hat ein Viertakt-Benzinmotor, der 200 Nm aus 2 Litern Hubraum erzeugt, einen MEP von (4π) (200 Nm) / (0,002 m³) = 1256000 Pa = 12 bar. Wie zu sehen ist, ist der Abgeordnete nützliche Eigenschaften eines Motors . Bei zwei Motoren mit gleichem Hubraum würde der Motor mit einem höheren MEP das größere Netz und, wenn die Motoren mit der gleichen Drehzahl laufen, eine größere Leistung erzeugen .

Otto-Zyklus – Problem mit der Lösung

Nehmen wir den Otto-Zyklus an , der einer der häufigsten thermodynamischen Zyklen ist, die in Automotoren zu finden sind . Einer der Schlüsselparameter solcher Motoren ist die Volumenänderung zwischen dem oberen Totpunkt (OT) und dem unteren Totpunkt (BDC). Das Verhältnis dieser Volumina ( V ₁ / V ₂ ) ist als Kompressionsverhältnis bekannt .

Das Verdichtungsverhältnis in einem benzinbetriebenen Motor ist aufgrund eines möglichen Motorklopfens (Selbstentzündung) normalerweise nicht viel höher als 10: 1 und nicht niedriger als 6: 1. Beispielsweise können einige Sportwagenmotoren ein Verdichtungsverhältnis von bis zu 12,5: 1 haben (z. B. Ferrari 458 Italia).

In diesem Beispiel sei ein Otto-Zyklus mit einem Kompressionsverhältnis von CR = 9: 1 angenommen . Die Ansaugluft hat 100 kPa = 1 bar, 20 ° C und das Volumen der Kammer beträgt 500 cm³ vor dem Kompressionshub. Die Temperatur am Ende der adiabatischen Expansion beträgt T ₄ = 800 K.

• Spezifische Wärmekapazität bei konstantem Luftdruck bei Atmosphärendruck und Raumtemperatur: c _p = 1,01 kJ / kgK.
• Spezifische Wärmekapazität bei konstantem Luftvolumen bei Atmosphärendruck und Raumtemperatur: c _v = 0,718 kJ / kgK.
• κ = c _p / c _v = 1,4

Berechnung:

1. die Masse der Ansaugluft
2. die Temperatur T ₃
3. der Druck p ₃
4. die Wärmemenge, die durch Verbrennen des Kraftstoff-Luft-Gemisches zugeführt wird
5. der thermische Wirkungsgrad dieses Zyklus
6. der Europaabgeordnete

Lösung:

1)  die Masse der Ansaugluft

Zu Beginn der Berechnungen müssen wir die Gasmenge in der Flasche vor dem Kompressionshub bestimmen. Mit dem idealen Gasgesetz können wir die Masse finden:

pV = mR- _spezifisches T.

wo:

• p ist der absolute Druck des Gases
• m ist die Masse der Substanz
• T ist die absolute Temperatur
• V ist die Lautstärke
• R _spezifisch  ist die spezifische Gaskonstante, die gleich der universellen Gaskonstante geteilt durch die Molmasse (M) des Gases oder Gemisches ist. Für trockene Luft R _spezifisch = 287,1 J.kg ^-1 .K ^-1 .

deshalb

m = p ₁ V ₁ / R _spezifisch T ₁ = (100000 × 500 × 10 ^–6 ) / (287,1 × 293) = 5,95 × 10 ^–4 kg

In diesem Problem sind alle Volumes bekannt:

• V ₁ = V ₄ = V _max = 500 × 10 ^–6 m ³ (0,5 l)
• V ₂ = V ₃ = V _min = V _max / CR = 55,56 × 10 ^–6 m ³

Beachten Sie, dass (V _max – V _min ) x Anzahl der Zylinder = Gesamtmotorhubraum.

2)  die Temperatur T ₃

Da der Prozess adiabatisch ist, können wir die folgende p, V, T-Beziehung für adiabatische Prozesse verwenden :

somit

T ₃ = T ₄ . CR ^{& kgr; – ​​1} = 800. 9 ^0,4 = 1926 K.

3)  der Druck p ₃

Auch hier können wir das ideale Gasgesetz verwenden , um den Druck zu Beginn des Arbeitstakts wie folgt zu ermitteln:

p ₃ = mR _spezifisch T ₃ / V ₃ = 5,95 × 10 ^–4 × 287,1 × 1926 / 55,56 × 10 ^–6 = 5920000 Pa = 59,2 bar

4)  die zugeführte Wärmemenge

Um die Wärmemenge zu berechnen, die durch Verbrennen des Kraftstoff-Luft-Gemisches Q _add hinzugefügt wird , müssen wir den ersten Hauptsatz der Thermodynamik für den isochoren Prozess verwenden , der Q _add = ∆U angibt , daher:

Q _add = mc _v (T ₃ – T ₂ )

Die Temperatur am Ende des Kompressionshubs kann unter Verwendung der Beziehung p, V, T für adiabatische Prozesse zwischen den Punkten 1 → 2 bestimmt werden.

T ₂ = T ₁ . CR ^{& kgr; – ​​1} = 293. 9 ^0,4 = 706 K.

dann

Q _add = mc _v (T ₃ – T ₂ ) = 5,95 × 10 ^–4 × 718 × 1220 = 521,2 J.

5)  der thermische Wirkungsgrad

Wärmewirkungsgrad für einen Otto-Zyklus:

Wie im vorherigen Abschnitt abgeleitet, ist der thermische Wirkungsgrad eines Otto-Zyklus eine Funktion des Kompressionsverhältnisses und von κ:

6)  der mittlere effektive Druck

Der Europaabgeordnete wurde definiert als:

In dieser Gleichung ist das Verschiebungsvolumen gleich V _max – V _min . Das Netzwerk für einen Zyklus kann anhand der zugeführten Wärme und des thermischen Wirkungsgrads berechnet werden:

W _net = Q _add . η _Otto = 521,2 × 0,5847 = 304,7 J
MEP = 304,7 / ( 500 × 10 ^–6 – 55,56 × 10 ^–6 ) = 685,6 kPa = 6,856 bar