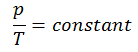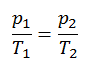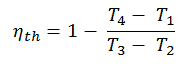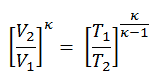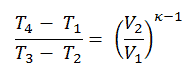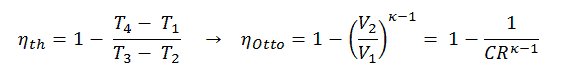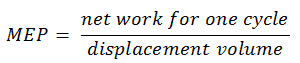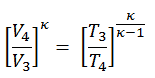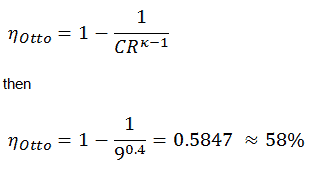Qu’est-ce que Cycle d’Otto – Définition

Cycle d’Otto – Processus

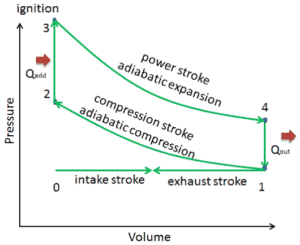
Dans un cycle Otto idéal, le système exécutant le cycle subit une série de quatre processus réversibles en interne: deux processus isentropiques (adiabatiques réversibles) alternés avec deux processus isochoriques:

1. Compression isentropique (course de compression) – Le gaz (mélange air-carburant) est comprimé adiabatiquement de l’état 1 à l’état 2, lorsque le piston se déplace du point mort bas au point mort haut. Les environs agissent sur le gaz, augmentant son énergie interne (température) et le compressant. En revanche, l’entropie reste inchangée. Les variations de volume et son rapport ( V ₁ / V ₂ ) sont connus comme le taux de compression.
2. Compression isochore (phase d’allumage) – Dans cette phase (entre l’état 2 et l’état 3), il y a un transfert de chaleur à volume constant (le piston est au repos) vers l’air à partir d’une source externe tandis que le piston est au repos au point mort haut . Ce processus est destiné à représenter l’inflammation du mélange carburant-air injecté dans la chambre et la combustion rapide qui en résulte. La pression augmente et le rapport ( P ₃ / P ₂ ) est appelé «rapport d’explosion».
3. Expansion isentropique (course de puissance) – Le gaz se détend adiabatiquement de l’état 3 à l’état 4, lorsque le piston se déplace du point mort haut au point mort bas. Le gaz travaille sur l’environnement (piston) et perd une quantité d’énergie interne égale au travail qui quitte le système. Encore une fois, l’entropie reste inchangée. Le rapport volumique ( V ₄ / V ₃ ) est connu sous le nom de ration d’expansion isentropique, mais pour le cycle d’Otto, il est égal au taux de compression.
4. Décompression isochore (course d’échappement) – Dans cette phase, le cycle se termine par un processus à volume constant dans lequel la chaleur est rejetée de l’air tandis que le piston est au point mort bas. La pression du gaz de travail chute instantanément du point 4 au point 1. La soupape d’échappement s’ouvre au point 4. La course d’échappement survient directement après cette décompression. Lorsque le piston se déplace du point mort bas (point 1) au point mort haut (point 0) avec la soupape d’échappement ouverte, le mélange gazeux est évacué vers l’atmosphère et le processus recommence.

Pendant le cycle d’Otto, le travail est effectué sur le gaz par le piston entre les états 1 et 2 ( compression isentropique ). Le travail se fait par le gaz sur le piston entre les étapes 3 et 4 ( détente isentropique ). La différence entre le travail effectué par le gaz et le travail effectué sur le gaz est le travail net produit par le cycle et il correspond à la zone délimitée par la courbe du cycle. Le travail produit par le cycle multiplie la vitesse du cycle (cycles par seconde) par la puissance produite par le moteur Otto.

Cycle d’Otto – diagramme pV, Ts

Le cycle d’Otto est souvent tracé sur un diagramme pression-volume (diagramme pV ) et sur un diagramme température-entropie (diagramme Ts). Lorsqu’ils sont tracés sur un diagramme de volume de pression, les processus isochoriques suivent les lignes isochoriques pour le gaz (les lignes verticales), les processus adiabatiques se déplacent entre ces lignes verticales et la zone délimitée par la piste cyclable complète représente le travail total qui peut être effectué pendant une cycle.

Diagramme température-entropie (diagramme Ts ) dans lequel l’état thermodynamique est spécifié par un point sur un graphique avec une ou des entropies spécifiques comme axe horizontal et une température absolue (T) comme axe vertical. Les diagrammes Ts sont un outil utile et courant, notamment parce qu’il permet de visualiser le transfert de chaleur au cours d’un processus. Pour les processus réversibles (idéaux), l’aire sous la courbe Ts d’un processus est la chaleur transférée au système pendant ce processus.

Cycle Otto – Moteur à quatre temps

Le cycle Otto est un ensemble de processus utilisés par les moteurs à combustion interne à allumage commandé (cycles à deux ou quatre temps). Nikolaus August Otto a d’abord conçu ce qui est connu comme le moteur à quatre temps. Une course se réfère à la course complète du piston le long du cylindre, dans les deux sens. Par conséquent, chacun ne correspond pas à un processus thermodynamique unique donné dans le chapitre Cycle d’Otto – Processus.

Le moteur à quatre temps comprend:

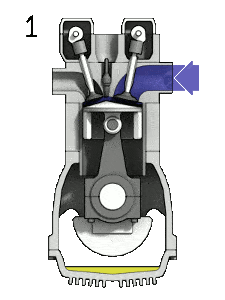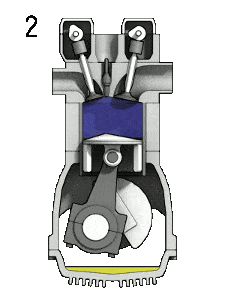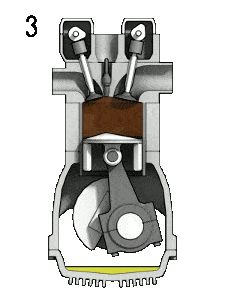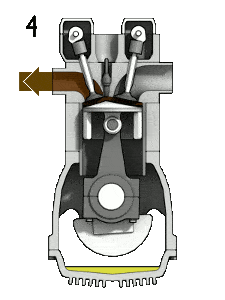
• la course d’admission – Le piston se déplace du point mort haut (PMH) au point mort bas (BDC) et le cycle passe les points 0 → 1. Dans cette course, la soupape d’admission est ouverte tandis que le piston tire un mélange air-carburant dans le cylindre en produisant une pression de vide dans le cylindre par son mouvement vers le bas.
• la course de compression – Le piston passe du point mort bas (BDC) au point mort haut (TDC) et le cycle passe aux points 1 → 2. Dans cette course, les soupapes d’admission et d’échappement sont fermées, donc le mélange air-carburant est comprimé. À la fin de cette course, le mélange air-carburant est enflammé par une étincelle, ce qui provoque une augmentation supplémentaire de la pression et de la température dans la chambre. À la fin de cette course, le vilebrequin a terminé une révolution complète de 360 ​​degrés.
• la course de puissance – Le piston passe du point mort haut (PMH) au point mort bas (BDC) et le cycle passe aux points 2 → 3 → 4. Dans cette course, les soupapes d’admission et d’échappement sont fermées. Au début de la course de puissance, une étincelle enflamme le mélange air-carburant dans la chambre de combustion, ce qui provoque à son tour une combustion très rapide du carburant. Dans cette course, le piston est entraîné vers le vilebrequin, le volume augmente et la pression diminue lorsque le travail est effectué par le gaz sur le piston.
• la course d’échappement. Le piston passe du point mort bas (BDC) au point mort haut (TDC) et le cycle passe aux points 4 → 1 → 0. Dans cette course, la soupape d’échappement est ouverte tandis que le piston tire les gaz d’échappement hors de la chambre. À la fin de cette course, le vilebrequin a terminé une deuxième révolution complète à 360 degrés.

Comparaison des cycles Otto réels et idéaux

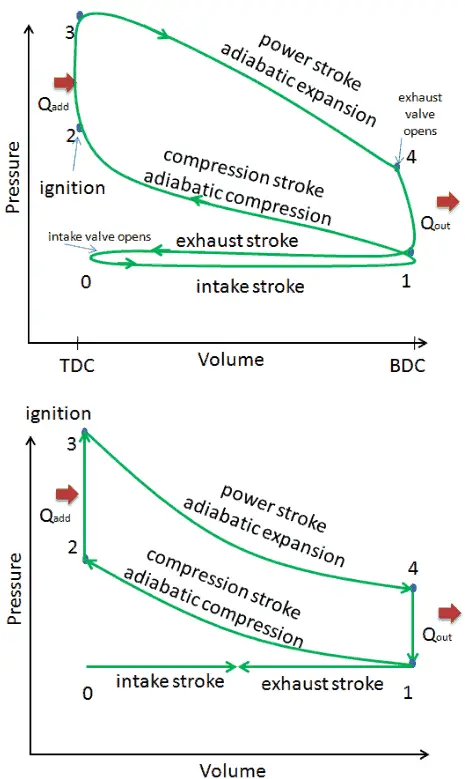Dans cette section, il est montré un cycle Otto idéal dans lequel il y a beaucoup d’ hypothèses différentes du cycle Otto réel . Les principales différences entre le moteur Otto réel et idéal apparaissent sur la figure. En réalité, le cycle idéal ne se produit pas et il y a de nombreuses pertes associées à chaque processus. Pour un cycle réel, la forme du diagramme pV est similaire à l’idéal, mais la zone (travail) entourée par le diagramme pV est toujours inférieure à la valeur idéale. Le cycle Otto idéal est basé sur les hypothèses suivantes:

• Cycle fermé.  La plus grande différence entre les deux diagrammes est la simplification des courses d’admission et d’échappement dans le cycle idéal. Dans la course d’échappement, la chaleur Q _out est éjectée dans l’environnement, dans un vrai moteur, le gaz quitte le moteur et est remplacé par un nouveau mélange d’air et de carburant.
• Ajout de chaleur instantané (ajout de chaleur isochore). Dans les moteurs réels, l’apport de chaleur n’est pas instantané, donc la pression de pointe n’est pas au PMH, mais juste après le PMH.
• Pas de transfert de chaleur (adiabatique)
  • Compression – Le gaz (mélange carburant-air) est comprimé de manière adiabatique de l’état 1 à l’état 2. Dans les moteurs réels, il y a toujours des inefficacités qui réduisent l’efficacité thermique.
  • Expansion. Le gaz (mélange carburant-air) se détend adiabatiquement de l’état 3 à l’état 4.
• Combustion complète du mélange air-carburant.
• Aucun travail de pompage . Le travail de pompage est la différence entre le travail effectué pendant la course d’échappement et le travail effectué pendant la course d’admission. Dans les cycles réels, il existe une différence de pression entre les pressions d’échappement et d’entrée.
• Aucune perte de purge . La perte de purge est causée par l’ouverture précoce des soupapes d’échappement. Il en résulte une perte de rendement de travail pendant la course d’expansion.
• Pas de perte par coup . La perte par soufflage est causée par la fuite de gaz comprimés à travers les segments de piston et autres crevasses.
• Pas de pertes par friction .

Ces hypothèses et pertes simplificatrices conduisent au fait que la zone fermée (travail) du diagramme pV pour un moteur réel est significativement plus petite que la taille de la zone (travail) incluse par le diagramme pV du cycle idéal. En d’autres termes, le cycle moteur idéal surestimera le travail net et, si les moteurs tournent à la même vitesse, une plus grande puissance produite par le moteur réel d’environ 20%.

Taux de compression – Otto Engine

Le taux de compression , CR , est défini comme le rapport du volume au point mort bas et du volume au point mort haut. Il s’agit d’une caractéristique clé pour de nombreux moteurs à combustion interne. Dans la section suivante, il sera montré que le taux de compression détermine l’ efficacité thermique du cycle thermodynamique utilisé du moteur à combustion. En général, on souhaite avoir un taux de compression élevé, car cela permet à un moteur d’atteindre une efficacité thermique plus élevée.

Par exemple, supposons un cycle Otto avec un taux de compression de CR = 10: 1. Le volume de la chambre est de 500 cm³ = 500 × 10 ^-6 m ³ (0,5 l) avant la course de compression. Pour ce moteur un ll requis volumes sont connus:

• V ₁ = V ₄ = V _max = 500 × 10 ^-6 m ³ (0,5 l)
• V ₂ = V ₃ = V _min = V _max / CR = 55,56 × 10 ^-6 m ³

Notez que (V _max – V _min ) x nombre de cylindres = cylindrée totale du moteur.

Exemples de taux de compression – essence vs diesel

• Le taux de compression dans un moteur à essence ne sera généralement pas beaucoup plus élevé que 10: 1 en raison du potentiel cognement du moteur (auto-inflammation) et pas inférieur à 6: 1 .
• Une Subaru Impreza WRX turbocompressée a un taux de compression de 8,0: 1 . En général, les moteurs turbocompressés ou suralimentés ont déjà de l’air comprimé à l’admission d’air, ils sont donc généralement construits avec un taux de compression plus faible.
• Un moteur Honda S2000 d’origine (F22C1) a un taux de compression de 11,1: 1 .
• Certains moteurs de voitures de sport atmosphériques peuvent avoir un taux de compression allant jusqu’à 12,5: 1 (par exemple Ferrari 458 Italia).
• En 2012, Mazda a lancé de nouveaux moteurs à essence sous la marque SkyActiv avec un taux de compression de 14: 1 . Pour réduire le risque de cognement du moteur, les gaz résiduels sont réduits en utilisant des systèmes d’échappement de moteur 4-2-1 , en mettant en place une cavité de piston et en optimisant l’injection de carburant.
• Les moteurs diesel ont un taux de compression qui dépasse normalement 14: 1 et des rapports supérieurs à 22: 1 sont également courants.

Efficacité thermique pour le cycle Otto

En général , le rendement thermique , η _e , d’un moteur thermique est définie comme étant le rapport entre le travail qu’elle fait, W , à la chaleur d’ entrée à la température élevée, Q _H .

L’ efficacité thermique , η _th , représente la fraction de chaleur , Q _H , qui est convertie en travail . Puisque l’énergie est conservée selon la première loi de la thermodynamique et que l’énergie ne peut pas être convertie pour fonctionner complètement, l’apport de chaleur, Q _H , doit être égal au travail effectué, W, plus la chaleur qui doit être dissipée sous forme de chaleur résiduelle Q _C dans le environnement. Par conséquent, nous pouvons réécrire la formule de l’efficacité thermique comme suit:

La chaleur absorbée se produit pendant la combustion du mélange carburant-air, lorsque l’étincelle se produit, à peu près à volume constant. Puisqu’au cours d’un processus isochore, aucun travail n’est effectué par ou sur le système, la première loi de la thermodynamique dicte ∆U = ∆Q. Par conséquent, la chaleur ajoutée et rejetée est donnée par:

Q _add = mc _v (T ₃ – T ₂ )

Q _out = mc _v (T ₄ – T ₁ )

En substituant ces expressions à la chaleur ajoutée et rejetée dans l’expression pour l’efficacité thermique, on obtient:

Nous pouvons simplifier l’expression ci-dessus en utilisant le fait que les processus 1 → 2 et de 3 → 4 sont adiabatiques et pour un processus adiabatique la formule p, V, T suivante est valide:

On peut déduire que:

Dans cette équation, le rapport V ₁ / V ₂ est appelé taux de compression CR . Lorsque nous réécrivons l’expression de l’efficacité thermique en utilisant le taux de compression, nous concluons que l’ efficacité thermique du cycle d’Otto standard de l’ air est fonction du taux de compression et de  κ = c _p / c _v .

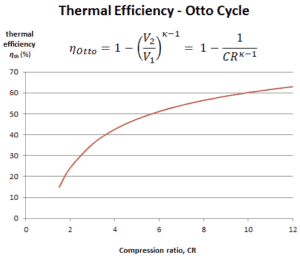
C’est une conclusion très utile, car il est souhaitable d’atteindre un taux de compression élevé pour extraire plus d’énergie mécanique d’une masse donnée de mélange air-carburant. Un taux de compression plus élevé permet d’atteindre la même température de combustion avec moins de carburant, tout en prolongeant le cycle de détente. Cela crée plus de puissance mécanique et abaisse la température d’échappement . L’abaissement de la température d’échappement provoque l’abaissement de l’énergie rejetée dans l’atmosphère. Cette relation est représentée sur la figure pour κ = 1,4, représentant l’air ambiant.

Auto-inflammation – Limite du taux de compression

Dans un moteur à essence ordinaire, le taux de compression a ses limites. Le taux de compression dans un moteur à essence ne sera généralement pas beaucoup plus élevé que 10: 1 en raison du potentiel cognement du moteur ( auto-inflammation ) et pas inférieur à 6: 1 . Des taux de compression plus élevés rendront cependant les moteurs à essence sujets aux cognements du moteur, causés par l’ auto-inflammation, un mélange non brûlé , si un carburant à indice d’octane inférieur est utilisé. Le mélange non brûlé peut s’auto-allumer en faisant exploser la pression et la chaleur uniquement, plutôt que de s’enflammer de la bougie d’allumage au bon moment. Le cliquetis du moteur peut être réduit en utilisant du carburant à indice d’octane élevé, ce qui augmente la résistance de l’essence à l’auto-inflammation . Plus l’indice d’octane est élevé, plus le carburant peut résister à la compression avant de détoner (s’enflammer). Puisque la température atteinte par le mélange air-carburant pendant la compression augmente à mesure que le taux de compression augmente, la probabilité d’auto-inflammation augmente avec le taux de compression. L’auto-inflammation peut réduire l’efficacité ou endommager le moteur si des capteurs de cliquetis ne sont pas présents pour modifier le calage de l’allumage.

Des taux de compression plus élevés peuvent être atteints dans les moteurs diesel (également appelés moteurs à allumage par compression ), car ils ne compressent pas le carburant, mais compressent uniquement l’air et injectent ensuite du carburant dans l’air qui a été chauffé par compression. Les taux de compression compris entre 12 et 20 sont typiques des moteurs diesel. La plus grande expansion des moteurs diesel signifie qu’ils rejettent moins de chaleur dans leur échappement plus froid. Le taux de compression plus élevé (expansion plus importante) et la température de pointe plus élevée font que les moteurs diesel atteignent une efficacité thermique plus élevée.

Pression efficace moyenne – MEP

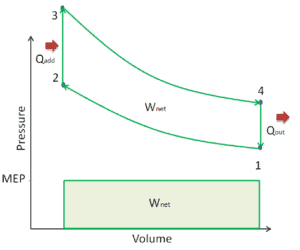
Un paramètre utilisé par les ingénieurs pour décrire les performances des moteurs à pistons alternatifs est connu sous le nom de pression effective moyenne , ou MEP . Le MEP est une mesure très utile de la capacité d’un moteur à effectuer un travail indépendant de la cylindrée du moteur. Il existe plusieurs types de députés européens. Ces eurodéputés sont définis par la mesure de l’emplacement et la méthode de calcul (par exemple BMEP ou IMEP).

En général, la pression efficace moyenne est la pression constante théorique qui, si elle agissait sur le piston pendant la course de puissance, produirait le même travail net que celui réellement développé en un cycle complet. Le MEP peut être défini comme:

Par exemple, la pression effective moyenne nette indiquée , connue sous le nom d’ IMEP _n, est égale à la pression effective moyenne calculée à partir de la pression dans le cylindre (il doit y avoir cette mesure) sur tout le cycle du moteur. Notez que c’est 720 ° pour un moteur à quatre temps et 360 ° pour un moteur à deux temps.

Quelques exemples:

• La MEP d’un moteur à essence atmosphérique peut varier de 8 à 11 bars dans la région du couple maximal.
• La MEP d’un moteur à essence turbocompressé peut varier de 12 à 17 bar.
• La MEP d’un moteur diesel atmosphérique peut aller de 7 à 9 bar.
• La MEP d’un moteur diesel turbocompressé peut aller de 14 à 18 bar

Par exemple, un moteur à essence à quatre temps produisant 200 N · m à partir de 2 litres de cylindrée a une MEP de (4π) (200 N · m) / (0,002 m³) = 1256000 Pa = 12 bar. Comme on peut le voir, le MEP est des caractéristiques utiles d’un moteur . Pour deux moteurs de cylindrée égale, celui avec un MEP plus élevé produirait le travail net plus important et, si les moteurs tournent à la même vitesse, une plus grande puissance .

Cycle d’Otto – Problème avec la solution

Supposons le cycle Otto , qui est l’un des cycles thermodynamiques les plus courants que l’on puisse trouver dans les moteurs d’automobiles . L’un des paramètres clés de ces moteurs est le changement de volume entre le point mort haut (TDC) et le point mort bas (BDC). Le rapport de ces volumes ( V ₁ / V ₂ ) est appelé taux de compression .

Le taux de compression dans un moteur à essence ne sera généralement pas beaucoup plus élevé que 10: 1 en raison du potentiel cognement du moteur (auto-inflammation) et pas inférieur à 6: 1. Par exemple, certains moteurs de voitures de sport peuvent avoir un taux de compression allant jusqu’à 12,5: 1 (par exemple Ferrari 458 Italia).

Dans cet exemple, supposons un cycle Otto avec un taux de compression de CR = 9: 1 . L’air d’admission est à 100 kPa = 1 bar, 20 ° C, et le volume de la chambre est de 500 cm³ avant la course de compression. La température en fin d’ expansion adiabatique est T ₄ = 800 K.

• Capacité thermique spécifique à pression d’air constante à pression atmosphérique et température ambiante: c _p = 1,01 kJ / kgK.
• Capacité calorifique spécifique à volume d’air constant à pression atmosphérique et température ambiante: c _v = 0,718 kJ / kgK.
• κ = c _p / c _v = 1,4

Calculer:

1. la masse d’air d’admission
2. la température T ₃
3. la pression p ₃
4. la quantité de chaleur ajoutée par la combustion du mélange air-carburant
5. l’efficacité thermique de ce cycle
6. le député européen

Solution:

1)  la masse d’air d’admission

Au début des calculs, nous devons déterminer la quantité de gaz dans le cylindre avant la course de compression. En utilisant la loi du gaz idéal, nous pouvons trouver la masse:

pV = mR _spécifique T

où:

• p est la pression absolue du gaz
• m est la masse de substance
• T est la température absolue
• V est le volume
• R _spécifique  est la constante de gaz spécifique, égale à la constante de gaz universelle divisée par la masse molaire (M) du gaz ou du mélange. Pour l’air sec R _spécifique = 287,1 J.kg ^-1 .K ^-1 .

par conséquent

m = p ₁ V ₁ / R _spécifique T ₁ = (100000 × 500 × 10 ^-6 ) / (287,1 × 293) = 5,95 × 10 ^-4 kg

Dans ce problème, tous les volumes sont connus:

• V ₁ = V ₄ = V _max = 500 × 10 ^-6 m ³ (0,5 l)
• V ₂ = V ₃ = V _min = V _max / CR = 55,56 × 10 ^-6 m ³

Notez que (V _max – V _min ) x nombre de cylindres = cylindrée totale du moteur.

2)  la température T ₃

Puisque le processus est adiabatique, nous pouvons utiliser la relation p, V, T suivante pour les processus adiabatiques :

Donc

T ₃ = T ₄ . CR ^{κ – 1} = 800. 9 ^0,4 = 1926 K

3)  la pression p ₃

Encore une fois, nous pouvons utiliser la loi du gaz idéal pour trouver la pression au début de la course de puissance comme:

p ₃ = mR _spécifique T ₃ / V ₃ = 5,95 × 10 ^-4 x 287,1 x 1926 / 55,56 × 10 ^-6 = 5920000 Pa = 59,2 bar

4)  la quantité de chaleur ajoutée

Pour calculer la quantité de chaleur ajoutée par la combustion du mélange air-carburant, Q _add , nous devons utiliser la première loi de la thermodynamique pour le processus isochore , qui indique que Q _add = ∆U, donc:

Q _add = mc _v (T ₃ – T ₂ )

la température à la fin de la course de compression peut être déterminée en utilisant la relation p, V, T pour les processus adiabatiques entre les points 1 → 2.

T ₂ = T ₁ . CR ^{κ – 1} = 293. 9 ^0,4 = 706 K

ensuite

Q _add = mc _v (T ₃ – T ₂ ) = 5,95 × 10 ^-4 x 718 x 1220 = 521,2 J

5)  l’efficacité thermique

Efficacité thermique pour un cycle Otto:

Comme dérivé dans la section précédente, l’efficacité thermique d’un cycle d’Otto est fonction du taux de compression et de κ:

6)  la pression efficace moyenne

Le député européen a été défini comme:

Si cette équation, le volume de déplacement est égal à V _max – V _min . Le travail net pour un cycle peut être calculé en utilisant la chaleur ajoutée et l’efficacité thermique:

W _net = Q _add . η _Otto = 521,2 x 0,5847 = 304,7 J
MEP = 304,7 / ( 500 × 10 ^-6 – 55,56 × 10 ^-6 ) = 685,6 kPa = 6,856 bar

……………………………………………………………………………………………………………………………….

Cet article est basé sur la traduction automatique de l’article original en anglais. Pour plus d’informations, voir l’article en anglais. Pouvez vous nous aider Si vous souhaitez corriger la traduction, envoyez-la à l’adresse: translations@nuclear-power.com ou remplissez le formulaire de traduction en ligne. Nous apprécions votre aide, nous mettrons à jour la traduction le plus rapidement possible. Merci