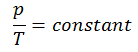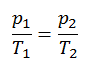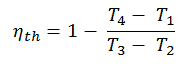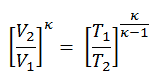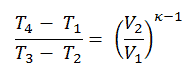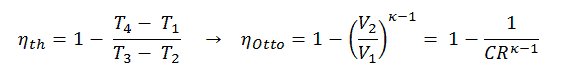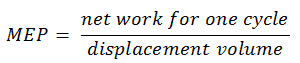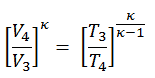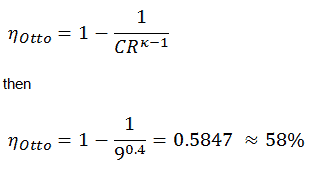Ciclo Otto – Motor Otto
En 1876, un ingeniero alemán, Nikolaus August Otto, avanzó el estudio de los motores térmicos mediante la construcción del primer motor de cuatro tiempos en funcionamiento. Un motor estacionario que utiliza una mezcla de carbón gas-aire como combustible. Wilhelm Maybach (1846-1929), uno de los ingenieros alemanes más importantes, perfeccionó la construcción, que ya se producía en grandes cantidades a finales del año 1876. Estos inventos reformaron rápidamente el mundo en el que vivían.
El ciclo del motor Otto se llama ciclo Otto. Es uno de los ciclos termodinámicos más comunes que se pueden encontrar en los motores de automóviles y describe el funcionamiento de un motor de pistón de encendido por chispa típico. A diferencia del ciclo de Carnot, el ciclo de Otto no ejecuta procesos isotérmicos, ya que estos deben realizarse muy lentamente. En un ciclo Otto ideal, el sistema que ejecuta el ciclo se somete a una serie de cuatro procesos reversibles internamente: dos procesos isentrópicos (adiabáticos reversibles) alternados con dos procesos isocróricos.
Dado que el principio de Carnot establece que ningún motor puede ser más eficiente que un motor reversible ( un motor térmico de Carnot ) que opera entre los mismos depósitos de alta temperatura y baja temperatura, el motor Otto debe tener una eficiencia menor que la eficiencia de Carnot. Un motor automotriz de gasolina típico opera alrededor del 25% al 30% de la eficiencia térmica. Aproximadamente 70-75% se rechaza como calor residual sin convertirse en trabajo útil, es decir, trabajo entregado a las ruedas.
Ciclo Otto – Procesos
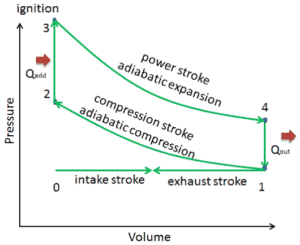
En un ciclo Otto ideal, el sistema que ejecuta el ciclo se somete a una serie de cuatro procesos reversibles internamente: dos procesos isentrópicos (adiabáticos reversibles) alternados con dos procesos isocróricos:
- Compresión isentrópica (carrera de compresión): el gas (mezcla de combustible y aire) se comprime adiabáticamente del estado 1 al estado 2, a medida que el pistón se mueve desde el punto muerto inferior al punto muerto superior. Los alrededores trabajan con el gas, aumentando su energía interna (temperatura) y comprimiéndolo. Por otro lado, la entropía permanece sin cambios. Los cambios en los volúmenes y su relación ( V 1 / V 2 ) se conocen como la relación de compresión.
- Compresión isocórica (fase de encendido): en esta fase (entre el estado 2 y el estado 3) hay una transferencia de calor de volumen constante (el pistón está en reposo) al aire desde una fuente externa mientras el pistón está en reposo en el punto muerto superior . Este proceso está destinado a representar la ignición de la mezcla de combustible y aire inyectada en la cámara y la posterior combustión rápida. La presión aumenta y la relación ( P 3 / P 2 ) se conoce como la “relación de explosión”.
- Expansión isentrópica (golpe de poder): el gas se expande adiabáticamente desde el estado 3 al estado 4, a medida que el pistón se mueve desde el punto muerto superior al punto muerto inferior. El gas funciona en el entorno (pistón) y pierde una cantidad de energía interna igual al trabajo que abandona el sistema. Nuevamente, la entropía permanece sin cambios. La relación de volumen ( V 4 / V 3 ) se conoce como la relación de expansión isentrópica, pero para el ciclo de Otto, es igual a la relación de compresión.
- Descompresión isocórica (carrera de escape) : en esta fase, el ciclo se completa con un proceso de volumen constante en el que el calor se rechaza del aire mientras el pistón está en el punto muerto inferior. La presión del gas de trabajo cae instantáneamente desde el punto 4 al punto 1. La válvula de escape se abre en el punto 4. La carrera de escape se produce directamente después de esta descompresión. A medida que el pistón se mueve desde el punto muerto inferior (punto 1) al punto muerto superior (punto 0) con la válvula de escape abierta, la mezcla gaseosa se ventila a la atmósfera y el proceso comienza de nuevo.
Durante el ciclo de Otto, el pistón trabaja en el gas entre los estados 1 y 2 ( compresión isentrópica ). El gas realiza el trabajo en el pistón entre las etapas 3 y 4 ( expansión isentrópica ). La diferencia entre el trabajo realizado por el gas y el trabajo realizado sobre el gas es el trabajo neto producido por el ciclo y corresponde al área encerrada por la curva del ciclo. El trabajo producido por el ciclo multiplicado por la velocidad del ciclo (ciclos por segundo) es igual a la potencia producida por el motor Otto.
Proceso isentrópico
Un proceso isentrópico es un proceso termodinámico , en el cual la entropía del fluido o gas permanece constante. Significa que el proceso isentrópico es un caso especial de un proceso adiabático en el que no hay transferencia de calor o materia. Es un proceso adiabático reversible . La suposición de que no hay transferencia de calor es muy importante, ya que podemos usar la aproximación adiabática solo en procesos muy rápidos .
Proceso isentrópico y la primera ley
Para un sistema cerrado, podemos escribir la primera ley de la termodinámica en términos de entalpía :
dH = dQ + Vdp
o
dH = TdS + Vdp
Proceso isentrópico (dQ = 0):
dH = Vdp → W = H 2 – H 1 → H 2 – H 1 = C p (T 2 – T 1 ) (para gas ideal )
Proceso isentrópico del gas ideal
El proceso isentrópico (un caso especial de proceso adiabático) se puede expresar con la ley de los gases ideales como:
pV κ = constante
o
p 1 V 1 κ = p 2 V 2 κ
en el que κ = c p / c v es la relación de los calores específicos (o capacidades de calor ) para el gas. Uno para presión constante (c p ) y otro para volumen constante (c v ) . Tenga en cuenta que esta relación κ = c p / c v es un factor para determinar la velocidad del sonido en un gas y otros procesos adiabáticos.
Proceso isocorico
Un proceso isocrórico es un proceso termodinámico, en el que el volumen del sistema cerrado permanece constante (V = constante). Describe el comportamiento del gas dentro del contenedor, que no puede deformarse. Dado que el volumen permanece constante, la transferencia de calor dentro o fuera del sistema no funciona con el p∆V , sino que solo cambia la energía interna (la temperatura) del sistema.
Proceso isocrórico y la primera ley
La forma clásica de la primera ley de la termodinámica es la siguiente ecuación:
dU = dQ – dW
En esta ecuación, dW es igual a dW = pdV y se conoce como el trabajo límite . Luego:
dU = dQ – pdV
En el proceso isocrórico y el gas ideal , todo el calor agregado al sistema se utilizará para aumentar la energía interna.
Proceso isocórico (pdV = 0):
dU = dQ (para gas ideal)
dU = 0 = Q – W → W = Q (para gas ideal)
Proceso isocrórico del gas ideal
El proceso isocrórico se puede expresar con la ley de los gases ideales como:
o
En un diagrama pV , el proceso ocurre a lo largo de una línea horizontal que tiene la ecuación V = constante.
Ver también: Ley de Guy-Lussac
Ciclo Otto – pV, diagrama Ts

El ciclo de Otto a menudo se representa en un diagrama de presión-volumen (diagrama pV ) y en un diagrama de temperatura-entropía (diagrama Ts). Cuando se traza en un diagrama de volumen de presión, los procesos isocróricos siguen las líneas isocróricas para el gas (las líneas verticales), los procesos adiabáticos se mueven entre estas líneas verticales y el área delimitada por la ruta completa del ciclo representa el trabajo total que se puede hacer durante uno ciclo.
El diagrama de temperatura-entropía (diagrama Ts ) en el que el estado termodinámico se especifica mediante un punto en un gráfico con entropía específica (s) como eje horizontal y temperatura absoluta (T) como eje vertical. Los diagramas Ts son una herramienta útil y común, particularmente porque ayuda a visualizar la transferencia de calor durante un proceso. Para procesos reversibles (ideales), el área bajo la curva Ts de un proceso es el calor transferido al sistema durante ese proceso.
Otto Cycle – Motor de cuatro tiempos
El ciclo Otto es un conjunto de procesos utilizados por los motores de combustión interna de encendido por chispa (ciclos de dos o cuatro tiempos). Nikolaus August Otto diseñó por primera vez lo que se conoce como el motor de cuatro tiempos. Un golpe se refiere al recorrido completo del pistón a lo largo del cilindro, en cualquier dirección. Por lo tanto, cada uno no corresponde a un solo proceso termodinámico dado en el capítulo Ciclo Otto – Procesos.
El motor de cuatro tiempos comprende:
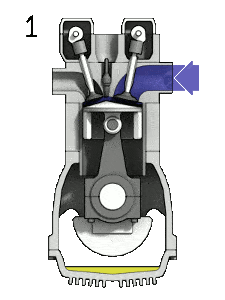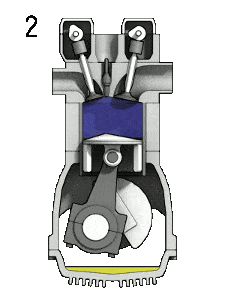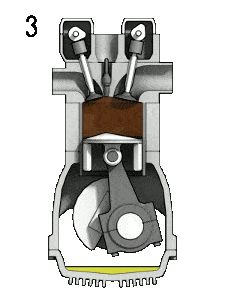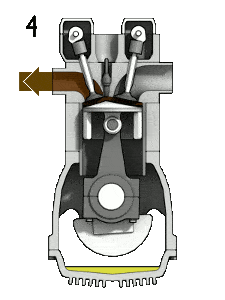
- la carrera de admisión: el pistón se mueve desde el punto muerto superior (TDC) al punto muerto inferior (BDC) y el ciclo pasa los puntos 0 → 1. En esta carrera, la válvula de admisión está abierta mientras el pistón introduce una mezcla de aire y combustible en el cilindro produciendo presión de vacío en el cilindro a través de su movimiento hacia abajo.
- la carrera de compresión: el pistón se mueve desde el punto muerto inferior (BDC) al punto muerto superior (TDC) y el ciclo pasa los puntos 1 → 2. En esta carrera, las válvulas de admisión y escape están cerradas, por lo tanto, la mezcla de combustible y aire se comprime. Al final de esta carrera, la mezcla de combustible y aire se enciende mediante una chispa, lo que provoca un mayor aumento de la presión y la temperatura en la cámara. Al final de este golpe, el cigüeñal ha completado una revolución completa de 360 grados.
- la carrera de potencia: el pistón se mueve desde el punto muerto superior (TDC) al punto muerto inferior (BDC) y el ciclo pasa los puntos 2 → 3 → 4. En esta carrera, las válvulas de admisión y escape están cerradas. Al comienzo de la carrera de potencia, una chispa enciende la mezcla de combustible y aire en la cámara de combustión, lo que a su vez provoca una combustión muy rápida del combustible. En esta carrera, el pistón se dirige hacia el cigüeñal, el volumen aumenta y la presión cae a medida que el gas realiza el trabajo en el pistón.
- La carrera de escape. El pistón se mueve desde el punto muerto inferior (BDC) al punto muerto superior (TDC) y el ciclo pasa los puntos 4 → 1 → 0. En esta carrera, la válvula de escape está abierta mientras el pistón extrae los gases de escape de la cámara. Al final de este golpe, el cigüeñal ha completado una segunda revolución completa de 360 grados.
Comparación de los ciclos reales e ideales de Otto
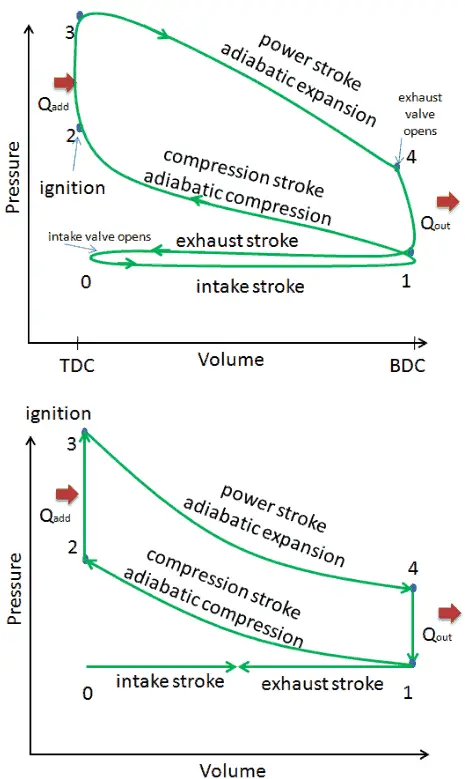 En esta sección, se muestra un ciclo ideal de Otto en el que hay muchos supuestos que difieren del ciclo real de Otto . Las principales diferencias entre el motor Otto real e ideal aparecen en la figura. En realidad, el ciclo ideal no ocurre y hay muchas pérdidas asociadas con cada proceso. Para un ciclo real, la forma del diagrama pV es similar al ideal, pero el área (trabajo) encerrada por el diagrama pV es siempre menor que el valor ideal. El ciclo ideal de Otto se basa en los siguientes supuestos:
En esta sección, se muestra un ciclo ideal de Otto en el que hay muchos supuestos que difieren del ciclo real de Otto . Las principales diferencias entre el motor Otto real e ideal aparecen en la figura. En realidad, el ciclo ideal no ocurre y hay muchas pérdidas asociadas con cada proceso. Para un ciclo real, la forma del diagrama pV es similar al ideal, pero el área (trabajo) encerrada por el diagrama pV es siempre menor que el valor ideal. El ciclo ideal de Otto se basa en los siguientes supuestos:
- Ciclo cerrado. La mayor diferencia entre los dos diagramas es la simplificación de las carreras de admisión y escape en el ciclo ideal. En la carrera de escape, el calor Q a cabo se expulsa al medio ambiente, en un motor real, las hojas de gas del motor y se sustituye por una nueva mezcla de aire y combustible.
- Adición de calor instantáneo (adición de calor isocrórico). En motores reales, la adición de calor no es instantánea, por lo tanto, la presión máxima no está en TDC, sino justo después de TDC.
- Sin transferencia de calor (adiabático)
- Compresión: el gas (mezcla de combustible y aire) se comprime adiabáticamente del estado 1 al estado 2. En los motores reales, siempre hay algunas ineficiencias que reducen la eficiencia térmica.
- Expansión. El gas (mezcla de combustible y aire) se expande adiabáticamente del estado 3 al estado 4.
- Combustión completa de la mezcla de combustible y aire.
- Sin trabajo de bombeo . El trabajo de bombeo es la diferencia entre el trabajo realizado durante la carrera de escape y el trabajo realizado durante la carrera de admisión. En ciclos reales, hay una diferencia de presión entre las presiones de escape y de entrada.
- Sin pérdida por purga . La pérdida por purga es causada por la apertura temprana de las válvulas de escape. Esto da como resultado una pérdida de producción de trabajo durante la carrera de expansión.
- Sin pérdidas por golpe . La pérdida por soplado es causada por la fuga de gases comprimidos a través de anillos de pistón y otras grietas.
- Sin pérdidas por fricción .
Estas suposiciones y pérdidas simplificadoras conducen al hecho de que el área cerrada (trabajo) del diagrama pV para un motor real es significativamente menor que el tamaño del área (trabajo) encerrada en el diagrama pV del ciclo ideal. En otras palabras, el ciclo ideal del motor sobreestimará el trabajo neto y, si los motores funcionan a la misma velocidad, una mayor potencia producida por el motor real en aproximadamente un 20%.
Relación de compresión – Motor Otto
La relación de compresión , CR , se define como la relación del volumen en el punto muerto inferior y el volumen en el punto muerto superior. Es una característica clave para muchos motores de combustión interna. En la siguiente sección, se mostrará que la relación de compresión determina la eficiencia térmica del ciclo termodinámico usado del motor de combustión. En general, se desea tener una alta relación de compresión, ya que permite que un motor alcance una mayor eficiencia térmica.
Por ejemplo, supongamos un ciclo Otto con una relación de compresión de CR = 10: 1. El volumen de la cámara es de 500 cm³ = 500 × 10 -6 m 3 (0.5l) antes de la carrera de compresión. Para este motor un ll requiere volúmenes son conocidos:
- V 1 = V 4 = V máx = 500 × 10 -6 m 3 (0.5l)
- V 2 = V 3 = V min = V max / CR = 55,56 × 10 -6 m 3
Tenga en cuenta que (V max – V min ) x número de cilindros = desplazamiento total del motor.
Ejemplos de relaciones de compresión: gasolina versus diesel
- La relación de compresión en un motor de gasolina generalmente no será mucho mayor que 10: 1 debido a un potencial golpe del motor (autoencendido) y no menor a 6: 1 .
- Un Subaru Impreza WRX turboalimentado tiene una relación de compresión de 8.0: 1 . En general, los motores turboalimentados o sobrealimentados ya tienen aire comprimido en la entrada de aire, por lo tanto, generalmente están construidos con una relación de compresión menor.
- Un motor Honda S2000 estándar (F22C1) tiene una relación de compresión de 11.1: 1 .
- Algunos motores deportivos deportivos pueden tener una relación de compresión de hasta 12.5: 1 (por ejemplo, Ferrari 458 Italia).
- En 2012, Mazda lanzó nuevos motores de gasolina bajo la marca SkyActiv con una relación de compresión de 14: 1 . Para reducir el riesgo de golpe del motor, el gas residual se reduce mediante el uso de sistemas de escape del motor 4-2-1 , implementando una cavidad de pistón y optimizando la inyección de combustible.
- Los motores Diesel tienen una relación de compresión que normalmente supera 14: 1 y también son comunes relaciones superiores a 22: 1.
Eficiencia térmica para el ciclo Otto
En general, la eficiencia térmica , η º , de cualquier motor de calor se define como la relación de la obra lo hace, W , para el calor de entrada a la alta temperatura, Q H .
La eficiencia térmica , η th , representa la fracción de calor , Q H , que se convierte en trabajo . Dado que la energía se conserva de acuerdo con la primera ley de la termodinámica y la energía no se puede convertir para trabajar por completo, la entrada de calor, Q H , debe ser igual al trabajo realizado, W, más el calor que se debe disipar como calor residual Q C en el ambiente. Por lo tanto, podemos reescribir la fórmula para la eficiencia térmica como:
El calor absorbido ocurre durante la combustión de la mezcla de combustible y aire, cuando se produce la chispa, aproximadamente a un volumen constante. Dado que durante un proceso isocrórico no hay trabajo realizado por o sobre el sistema, la primera ley de la termodinámica dicta ∆U = ∆Q. Por lo tanto, el calor agregado y rechazado están dados por:
Q add = mc v (T 3 – T 2 )
Q out = mc v (T 4 – T 1 )
Sustituyendo estas expresiones por el calor agregado y rechazado en la expresión por rendimientos de eficiencia térmica:
Podemos simplificar la expresión anterior usando el hecho de que los procesos 1 → 2 y de 3 → 4 son adiabáticos y para un proceso adiabático la siguiente fórmula p, V, T es válida:
Se puede derivar que:
En esta ecuación, la relación V 1 / V 2 se conoce como la relación de compresión, CR . Cuando reescribimos la expresión de eficiencia térmica usando la relación de compresión, concluimos que la eficiencia térmica del ciclo Otto estándar de aire es una función de la relación de compresión y κ = c p / c v .
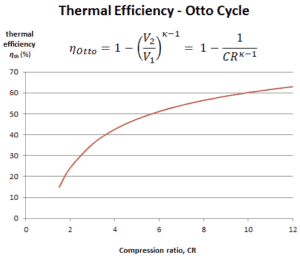
Es una conclusión muy útil, porque es deseable lograr una alta relación de compresión para extraer más energía mecánica de una masa dada de mezcla aire-combustible. Una relación de compresión más alta permite alcanzar la misma temperatura de combustión con menos combustible, al tiempo que proporciona un ciclo de expansión más largo. Esto crea más potencia mecánica y reduce la temperatura de escape . Disminuir la temperatura de escape provoca la disminución de la energía rechazada a la atmósfera. Esta relación se muestra en la figura para κ = 1.4, que representa el aire ambiente.
Autoinflamación: límite para la relación de compresión
En un motor de gasolina común, la relación de compresión tiene sus límites. La relación de compresión en un motor de gasolina generalmente no será mucho mayor que 10: 1 debido a un potencial golpe del motor ( autoencendido ) y no menor a 6: 1 . Sin embargo, las relaciones de compresión más altas harán que los motores de gasolina estén sujetos a golpes de motor, causados por la autoignición de una mezcla no quemada , si se usa combustible de menor octanaje. La mezcla no quemada puede autoignificarse detonando solo por presión y calor, en lugar de encenderse desde la bujía exactamente en el momento correcto. El golpeteo del motor se puede reducir mediante el uso de combustible de alto octanaje, lo que aumenta la resistencia de la gasolina a la autoignición . Cuanto más alto es el número de octano, más compresión puede soportar el combustible antes de detonar (encenderse). Dado que la temperatura alcanzada por la mezcla de combustible y aire durante la compresión aumenta a medida que aumenta la relación de compresión, la probabilidad de autoignición aumenta con la relación de compresión. La autoignición puede reducir la eficiencia o dañar el motor si no hay sensores de detonación para modificar la sincronización del encendido.
Se pueden lograr relaciones de compresión más altas en motores diesel (también conocidos como motores de encendido por compresión ), porque no comprimen el combustible, sino que comprimen solo aire y luego inyectan combustible en el aire que se calentó por compresión. Las relaciones de compresión en el rango de 12 a 20 son típicas para motores diesel. La mayor expansión en los motores diesel significa que rechazan menos calor en su escape más frío. La relación de compresión más alta (mayor expansión) y la temperatura máxima más alta hacen que los motores diesel alcancen una mayor eficiencia térmica.
Presión efectiva media – MEP
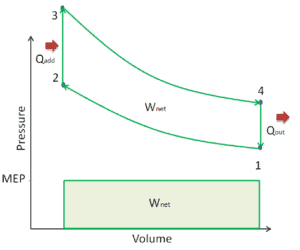
Un parámetro utilizado por los ingenieros para describir el rendimiento de los motores de pistón alternativo se conoce como presión efectiva media , o MEP . MEP es una medida muy útil de la capacidad de un motor para realizar trabajos que es independiente del desplazamiento del motor. Hay varios tipos de eurodiputados. Estos MEP se definen por la medición de la ubicación y el método de cálculo (por ejemplo, BMEP o IMEP).
En general, la presión efectiva media es la presión constante teórica que, si actuara sobre el pistón durante la carrera de potencia, produciría el mismo trabajo neto que realmente se desarrolla en un ciclo completo. El MEP se puede definir como:
Por ejemplo, la presión efectiva media neta indicada , conocida como IMEP n, es igual a la presión efectiva media calculada a partir de la presión dentro del cilindro (debe haber esta medición) durante todo el ciclo del motor. Tenga en cuenta que es 720 ° para un motor de cuatro tiempos y 360 ° para un motor de dos tiempos.
Algunos ejemplos:
- El MEP de un motor de gasolina atmosférico puede variar de 8 a 11 bar en la región de par máximo.
- El MEP de un motor de gasolina turboalimentado puede variar de 12 a 17 bar.
- El MEP de un motor diesel atmosférico puede variar de 7 a 9 bar.
- El MEP de un motor diesel turboalimentado puede variar de 14 a 18 bar
Por ejemplo, un motor de gasolina de cuatro tiempos que produce 200 N · m de 2 litros de desplazamiento tiene un MEP de (4π) (200 N · m) / (0.002 m³) = 1256000 Pa = 12 bar. Como se puede ver, el MEP es características útiles de un motor . Para dos motores de igual volumen de desplazamiento, el que tenga un MEP más alto produciría el mayor trabajo neto y, si los motores funcionan a la misma velocidad, mayor potencia .
Ciclo Otto – Problema con la solución
Supongamos el ciclo Otto , que es uno de los ciclos termodinámicos más comunes que se pueden encontrar en los motores de automóviles . Uno de los parámetros clave de tales motores es el cambio en los volúmenes entre el punto muerto superior (TDC) y el punto muerto inferior (BDC). La relación de estos volúmenes ( V 1 / V 2 ) se conoce como la relación de compresión .
La relación de compresión en un motor de gasolina generalmente no será mucho mayor que 10: 1 debido a posibles golpes del motor (autoencendido) y no menor a 6: 1. Por ejemplo, algunos motores de autos deportivos pueden tener una relación de compresión de hasta 12.5: 1 (por ejemplo, Ferrari 458 Italia).

En este ejemplo, supongamos un ciclo Otto con una relación de compresión de CR = 9: 1 . El aire de admisión está a 100 kPa = 1 bar, 20 ° C, y el volumen de la cámara es de 500 cm³ antes de la carrera de compresión. La temperatura al final de la expansión adiabática es T 4 = 800 K.
- Capacidad calorífica específica a presión constante del aire a presión atmosférica y temperatura ambiente: c p = 1,01 kJ / kgK.
- Capacidad calorífica específica a volumen constante de aire a presión atmosférica y temperatura ambiente: c v = 0.718 kJ / kgK.
- κ = c p / c v = 1.4
Calcular:
- la masa de aire de admisión
- la temperatura T 3
- la presión p 3
- la cantidad de calor agregado al quemar la mezcla de combustible y aire
- la eficiencia térmica de este ciclo
- el eurodiputado
Solución:
1) la masa del aire de admisión
Al comienzo de los cálculos tenemos que determinar la cantidad de gas en el cilindro antes de la carrera de compresión. Usando la ley de los gases ideales, podemos encontrar la masa:
pV = mR específico T
dónde:
- p es la presión absoluta del gas
- m es la masa de sustancia
- T es la temperatura absoluta
- V es el volumen
- R específica es la constante de gas específica, igual a la constante de gas universal dividida por la masa molar (M) del gas o mezcla. Para aire seco R específico = 287.1 J.kg -1 .K -1 .
por lo tanto
m = p 1 V 1 / R específico T 1 = (100000 × 500 × 10-6 ) / (287.1 × 293) = 5.95 × 10 -4 kg
En este problema se conocen todos los volúmenes:
- V 1 = V 4 = V máx = 500 × 10 -6 m 3 (0.5l)
- V 2 = V 3 = V min = V max / CR = 55,56 × 10 -6 m 3
Tenga en cuenta que (V max – V min ) x número de cilindros = desplazamiento total del motor.
2) la temperatura T 3
Dado que el proceso es adiabático, podemos usar la siguiente relación p, V, T para procesos adiabáticos :
así
T 3 = T 4 . CR κ – 1 = 800. 9 0.4 = 1926 K
3) la presión p 3
Nuevamente, podemos usar la ley de gas ideal para encontrar la presión al comienzo de la carrera de potencia como:
p 3 = mR específico T 3 / V 3 = 5.95 × 10 -4 x 287.1 x 1926 / 55.56 × 10 -6 = 5920000 Pa = 59.2 bar
4) la cantidad de calor agregado
Para calcular la cantidad de calor agregado al quemar la mezcla de combustible y aire, Q add , tenemos que usar la primera ley de la termodinámica para el proceso isocrórico , que establece que Q add = ∆U, por lo tanto:
Q add = mc v (T 3 – T 2 )
La temperatura al final de la carrera de compresión se puede determinar utilizando la relación p, V, T para procesos adiabáticos entre los puntos 1 → 2.
T 2 = T 1 . CR κ – 1 = 293. 9 0.4 = 706 K
luego
Q add = mc v (T 3 – T 2 ) = 5.95 × 10 -4 x 718 x 1220 = 521.2 J
5) la eficiencia térmica
Eficiencia térmica para un ciclo Otto:
Como se dedujo en la sección anterior, la eficiencia térmica de un ciclo Otto es una función de la relación de compresión y κ:
6) la presión efectiva media
El MEP se definió como:
En esta ecuación, el volumen de desplazamiento es igual a V max – V min . El trabajo neto para un ciclo se puede calcular utilizando el calor agregado y la eficiencia térmica:
W net = Q add . η Otto = 521.2 x 0.5847 = 304.7 J
MEP = 304.7 / ( 500 × 10-6 – 55.56 × 10 -6 ) = 685.6 kPa = 6.856 bar
……………………………………………………………………………………………………………………………….
Este artículo se basa en la traducción automática del artículo original en inglés. Para más información vea el artículo en inglés. Puedes ayudarnos. Si desea corregir la traducción, envíela a: translations@nuclear-power.com o complete el formulario de traducción en línea. Agradecemos su ayuda, actualizaremos la traducción lo antes posible. Gracias.