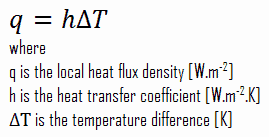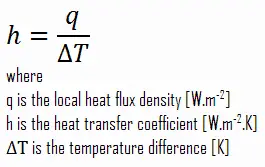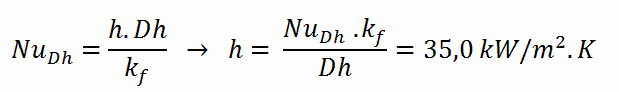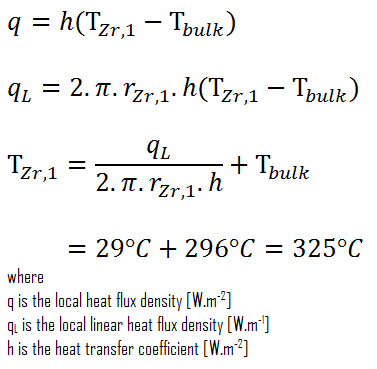Ley de enfriamiento de Newton
A pesar de la complejidad de la convección , se observa que la tasa de transferencia de calor por convección es proporcional a la diferencia de temperatura y se expresa convenientemente por la ley de enfriamiento de Newton , que establece que:
La tasa de pérdida de calor de un cuerpo es directamente proporcional a la diferencia de temperaturas entre el cuerpo y sus alrededores, siempre que la diferencia de temperatura sea pequeña y la naturaleza de la superficie radiante permanezca igual.
Tenga en cuenta que, ΔT viene dado por la temperatura de la superficie o la pared , la pared T y la temperatura total , T ∞ , que es la temperatura del fluido suficientemente lejos de la superficie.
Coeficiente de transferencia de calor convectivo
Como se puede ver, la constante de proporcionalidad será crucial en los cálculos y se conoce como el coeficiente de transferencia de calor por convección , h . El coeficiente de transferencia de calor por convección, h, se puede definir como:
La velocidad de transferencia de calor entre una superficie sólida y un fluido por unidad de superficie por unidad de diferencia de temperatura.
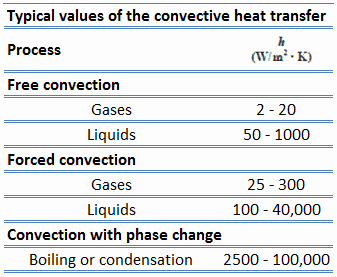 El coeficiente de transferencia de calor por convección depende de las propiedades físicas del fluido y la situación física. El coeficiente de transferencia de calor por convección no es una propiedad del fluido. Es un parámetro determinado experimentalmente cuyo valor depende de todas las variables que influyen en la convección, como la geometría de la superficie , la naturaleza del movimiento del fluido , las propiedades del fluido y la velocidad del fluido a granel .
El coeficiente de transferencia de calor por convección depende de las propiedades físicas del fluido y la situación física. El coeficiente de transferencia de calor por convección no es una propiedad del fluido. Es un parámetro determinado experimentalmente cuyo valor depende de todas las variables que influyen en la convección, como la geometría de la superficie , la naturaleza del movimiento del fluido , las propiedades del fluido y la velocidad del fluido a granel .
Típicamente, el coeficiente de transferencia de calor por convección para flujo laminar es relativamente bajo en comparación con el coeficiente de transferencia de calor por convección para flujo turbulento . Esto se debe al flujo turbulento que tiene una capa de película de fluido estancada más delgada en la superficie de transferencia de calor.
Cabe señalar que esta capa de película de fluido estancada juega un papel crucial para el coeficiente de transferencia de calor por convección. Se observa que el fluido se detiene completamente en la superficie y asume una velocidad cero en relación con la superficie. Este fenómeno se conoce como la condición antideslizante y, por lo tanto, en la superficie, el flujo de energía ocurre puramente por conducción. Pero en las siguientes capas se producen movimientos de conducción y difusión de masa en el nivel molecular o macroscópico. Debido al movimiento de masa, la tasa de transferencia de energía es mayor. Como se escribió, la ebullición nucleadaen la superficie altera efectivamente esta capa estancada y, por lo tanto, la ebullición de los nucleados aumenta significativamente la capacidad de una superficie para transferir energía térmica al fluido a granel.
Un fenómeno similar ocurre para la temperatura. Se observa que la temperatura del fluido en la superficie y la superficie tendrá la misma temperatura en el punto de contacto. Este fenómeno se conoce como la condición de salto sin temperatura y es muy importante para la teoría de la ebullición de nucleados .
Los valores del coeficiente de transferencia de calor , h, se han medido y tabulado para los fluidos comúnmente encontrados y las situaciones de flujo que ocurren durante la transferencia de calor por convección.
Ejemplo: Ley de Enfriamiento de Newton
 De: Ejemplo – Transferencia de calor por convección
De: Ejemplo – Transferencia de calor por convección
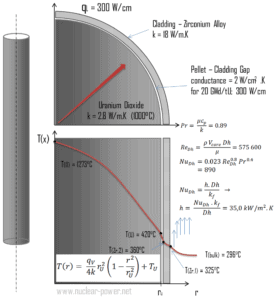
El conocimiento detallado de la geometría, los parámetros del fluido, el radio exterior del revestimiento, la tasa de calor lineal, el coeficiente de transferencia de calor por convección nos permite calcular la diferencia de temperatura ∆T entre el refrigerante (T volumen ) y la superficie del revestimiento (T Zr, 1 ).
Para calcular la temperatura de la superficie del revestimiento, debemos saber:
- El diámetro exterior del revestimiento es: d = 2 x r Zr, 1 = 9,3 mm
- el número de Nusselt, que es Nu Dh = 890
- El diámetro hidráulico del canal de combustible es: D h = 13,85 mm
- La conductividad térmica del refrigerante del reactor (300 ° C) es: k H2O = 0.545 W / mK
- La temperatura total del refrigerante del reactor en esta coordenada axial es: T mayor = 296 ° C
- La tasa de calor lineal del combustible es: q L = 300 W / cm (F Q ≈ 2.0)
El coeficiente de transferencia de calor por convección, h , viene dado directamente por la definición del número de Nusselt:
Finalmente, podemos calcular la temperatura de la superficie del revestimiento (T Zr, 1 ) simplemente usando la Ley de Enfriamiento de Newton :
Para los PWR en funcionamiento normal, hay un agua líquida comprimida dentro del núcleo del reactor, bucles y generadores de vapor. La presión se mantiene a aproximadamente 16MPa . A esta presión, el agua hierve a aproximadamente 350 ° C (662 ° F). Como se puede ver, la temperatura de la superficie T Zr, 1 = 325 ° C garantiza que ni siquiera se produce una ebullición subenfriada. Tenga en cuenta que, la ebullición subenfriada requiere T Zr, 1 = T sat . Dado que las temperaturas de entrada del agua suelen ser de unos 290 ° C (554 ° F), es obvio que este ejemplo corresponde a la parte inferior del núcleo. A elevaciones más altas del núcleo, la temperatura aparente puede alcanzar hasta 330 ° C. La diferencia de temperatura de 29 ° C hace que se produzca la ebullición subenfriada (330 ° C + 29 ° C> 350 ° C). Por otro lado, la ebullición de nucleados en la superficie altera efectivamente la capa estancada y, por lo tanto, la ebullición de nucleados aumenta significativamente la capacidad de una superficie para transferir energía térmica al fluido a granel. Como resultado, el coeficiente de transferencia de calor por convección aumenta significativamente y, por lo tanto, a elevaciones más altas, la diferencia de temperatura (T Zr, 1 – T a granel ) disminuye significativamente.
……………………………………………………………………………………………………………………………….
Este artículo se basa en la traducción automática del artículo original en inglés. Para más información vea el artículo en inglés. Puedes ayudarnos. Si desea corregir la traducción, envíela a: translations@nuclear-power.com o complete el formulario de traducción en línea. Agradecemos su ayuda, actualizaremos la traducción lo antes posible. Gracias.