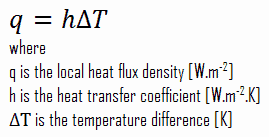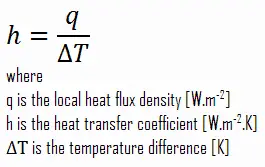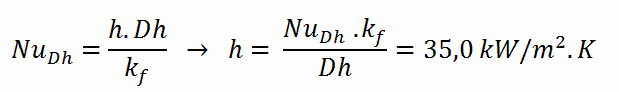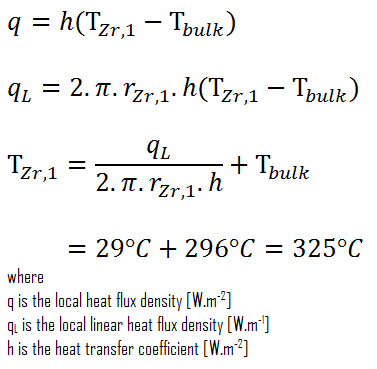Newtons Gesetz der Kühlung
Trotz der Komplexität der Konvektion wird beobachtet, dass die Geschwindigkeit der Konvektionswärmeübertragung proportional zur Temperaturdifferenz ist, und wird zweckmäßigerweise durch das Newtonsche Gesetz der Kühlung ausgedrückt , das besagt, dass:
Die Rate des Wärmeverlusts eines Körpers ist direkt proportional zum Temperaturunterschied zwischen dem Körper und seiner Umgebung, vorausgesetzt, der Temperaturunterschied ist gering und die Art der strahlenden Oberfläche bleibt gleich.
Man beachte , dass & Delta; T wird von der Oberfläche oder die gegebene Wandtemperatur , T Wand und die Massetemperatur , T ∞ , die die Temperatur des Fluids ist ausreichend weit von der Oberfläche.
Konvektiver Wärmeübergangskoeffizient
Wie zu sehen ist, die Konstante der Proportionalität wird in Berechnungen von entscheidender Bedeutung sein , und es ist bekannt als die Konvektionswärmeübergangskoeffizienten , h . Der konvektive Wärmedurchgangskoeffizient h kann wie folgt definiert werden:
Die Wärmeübertragungsrate zwischen einer festen Oberfläche und einem Fluid pro Oberflächeneinheit pro Temperaturunterschiedseinheit.
Der konvektive Wärmeübergangskoeffizient ist abhängig von den physikalischen Eigenschaften des Fluids und der physikalischen Situation. Der konvektive Wärmeübergangskoeffizient ist keine Eigenschaft der Flüssigkeit. Es ist ein experimentell ermittelter Parameter, dessen Wert von allen die Konvektion beeinflussenden Variablen abhängt, wie der Oberflächengeometrie , der Art der Fluidbewegung , den Eigenschaften des Fluids und der Volumenfluidgeschwindigkeit .
Typischerweise ist der konvektive Wärmeübertragungskoeffizient für laminare Strömung im Vergleich zum konvektiven Wärmeübertragungskoeffizienten für turbulente Strömung relativ niedrig . Dies ist auf eine turbulente Strömung mit einer dünneren Schicht aus stagnierendem Flüssigkeitsfilm auf der Wärmeübertragungsfläche zurückzuführen.
Es ist zu beachten, dass diese stagnierende Flüssigkeitsfilmschicht eine entscheidende Rolle für den konvektiven Wärmeübergangskoeffizienten spielt. Es wird beobachtet, dass die Flüssigkeit an der Oberfläche zum Stillstand kommt und eine Geschwindigkeit von Null in Bezug auf die Oberfläche annimmt. Dieses Phänomen ist als rutschfester Zustand bekannt, weshalb der Energiefluss an der Oberfläche ausschließlich durch Leitung erfolgt. In den nächsten Schichten treten jedoch sowohl Leitungs- als auch Diffusionsmassenbewegung auf molekularer oder makroskopischer Ebene auf. Aufgrund der Massenbewegung ist die Energieübertragungsrate höher. Wie geschrieben wurde, kocht der KernAn der Oberfläche wird diese stagnierende Schicht effektiv gestört, und daher erhöht das Sieden der Keime die Fähigkeit einer Oberfläche, Wärmeenergie auf das Schüttgut zu übertragen .
Ein ähnliches Phänomen tritt bei der Temperatur auf. Es wird beobachtet, dass die Temperatur des Fluids an der Oberfläche und die Oberfläche am Kontaktpunkt die gleiche Temperatur haben . Dieses Phänomen ist als Zustand ohne Temperatursprung bekannt und für die Theorie des Siedens von Keimen sehr wichtig .
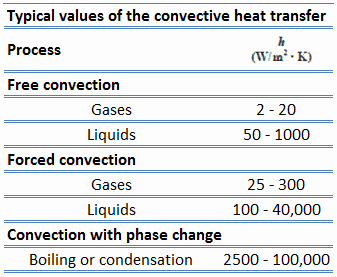
Die Werte des Wärmeübertragungskoeffizienten h wurden gemessen und für die häufig auftretenden Flüssigkeiten und Strömungssituationen, die während der Wärmeübertragung durch Konvektion auftreten, tabellarisch aufgeführt.
Beispiel: Newtons Gesetz der Kühlung
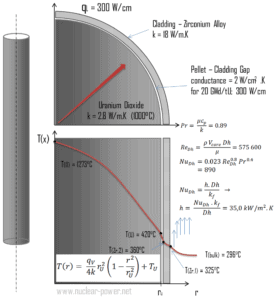Aus: Beispiel – Konvektive Wärmeübertragung
Detaillierte Kenntnisse der Geometrie, der Fluidparameter, des Außenmantelradius, der linearen Heizrate und des konvektiven Wärmeübertragungskoeffizienten ermöglichen die Berechnung der Temperaturdifferenz ∆T zwischen dem Kühlmittel (T- Volumen ) und der Manteloberfläche (T Zr, 1 ).
Um die Plattentemperatur zu berechnen, müssen wir wissen:
- der Außendurchmesser der Ummantelung beträgt: d = 2 x r Zr, 1 = 9,3 mm
- die Nusselt-Zahl, die Nu Dh = 890 ist
- Der hydraulische Durchmesser des Kraftstoffkanals beträgt: D h = 13,85 mm
- Die Wärmeleitfähigkeit des Reaktorkühlmittels (300 ° C) beträgt: k H 2 O = 0,545 W / mK
- Die Massentemperatur des Reaktorkühlmittels bei dieser axialen Koordinate beträgt: T Volumen = 296 ° C.
- Die lineare Heizrate des Brennstoffs beträgt: q L = 300 W / cm (F Q ≈ 2,0)
Der konvektive Wärmeübergangskoeffizient h wird direkt durch die Definition der Nusselt-Zahl angegeben:
Schließlich können wir die Temperatur der Manteloberfläche (T Zr, 1 ) einfach nach dem Newtonschen Gesetz der Kühlung berechnen :
Bei PWRs im Normalbetrieb befindet sich im Reaktorkern, in den Kreisläufen und in den Dampferzeugern komprimiertes flüssiges Wasser . Der Druck wird bei ungefähr 16 MPa gehalten . Bei diesem Druck kocht Wasser bei ungefähr 350 ° C (662 ° F). Wie zu sehen ist, stellt die Oberflächentemperatur T Zr, 1 = 325 ° C sicher, dass auch unterkühltes sieden nicht auftritt. Es ist zu beachten, dass unterkühltes sieden T Zr erfordert , 1 = T sat . Da die Einlasstemperaturen des Wassers üblicherweise ca. 290 ° C betragen (554 ° F) ist es offensichtlich, dass dieses Beispiel dem unteren Teil des Kerns entspricht. In höheren Lagen des Kerns kann die Massentemperatur bis zu 330 ° C erreichen. Der Temperaturunterschied von 29 ° C führt dazu, dass unterkühltes sieden auftreten kann (330 ° C + 29 ° C> 350 ° C). Andererseits stört das sieden von Keimen an der Oberfläche die stagnierende Schicht effektiv, und daher erhöht das sieden von Keimen die Fähigkeit einer Oberfläche, Wärmeenergie auf Schüttgut zu übertragen, erheblich . Infolgedessen steigt der konvektive Wärmeübergangskoeffizient signifikant an und daher nimmt in höheren Lagen die Temperaturdifferenz (T Zr, 1 – T Volumen ) signifikant ab.
……………………………………………………………………………………………………………………………….
Dieser Artikel basiert auf der maschinellen Übersetzung des englischen Originalartikels. Weitere Informationen finden Sie im Artikel auf Englisch. Sie können uns helfen. Wenn Sie die Übersetzung korrigieren möchten, senden Sie diese bitte an: translations@nuclear-power.com oder füllen Sie das Online-Übersetzungsformular aus. Wir bedanken uns für Ihre Hilfe und werden die Übersetzung so schnell wie möglich aktualisieren. Danke.
