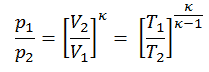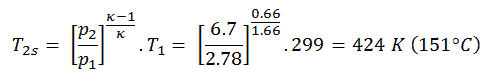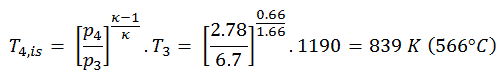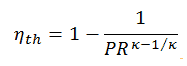Ciclo de Brayton: problema con la solución
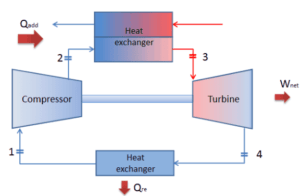Supongamos el ciclo cerrado de Brayton , que es uno de los ciclos termodinámicos más comunes que se pueden encontrar en los motores modernos de turbina de gas. En este caso, suponga una turbina de gas helio con compresor único y disposición de turbina única. Uno de los parámetros clave de tales motores es la temperatura máxima de entrada de la turbina y la relación de presión del compresor (PR = p 2 / p 1 ) que determina la eficiencia térmica de dicho motor.
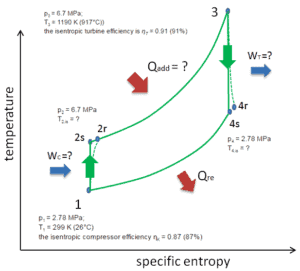
En esta turbina, la etapa de alta presión recibe gas (punto 3 en la figura) de un intercambiador de calor:
- p 3 = 6,7 MPa;
- T 3 = 1190 K (917 ° C))
- la eficiencia de la turbina isentrópica es η T = 0.91 (91%)
y expulsarlo a otro intercambiador de calor, donde la presión de salida es (punto 4):
- p 4 = 2.78 MPa
- T 4, es =?
Por lo tanto, la relación de presión del compresor es igual a PR = 2.41. Además, sabemos que el compresor recibe gas (punto 1) en la figura:
- p 1 = 2,78 MPa;
- T 1 = 299 K (26 ° C)
- La eficiencia del compresor isentrópico η K = 0.87 (87%).
La relación de capacidad calorífica, para helio es igual a = c p / c v = 1.66
Calcular:
- El calor agregado por el intercambiador de calor (entre 2 → 3)
- la temperatura de salida del compresor del gas (T 2, es )
- El verdadero trabajo realizado en este compresor, cuando la eficiencia del compresor isentrópico es η K = 0.87 (87%)
- la temperatura de salida de la turbina del gas (T 4, es )
- El trabajo real realizado por esta turbina, cuando la eficiencia de la turbina isentrópica es η T = 0.91 (91%)
- la eficiencia térmica de este ciclo
Solución:
1) + 2)
A partir de la primera ley de la termodinámica , el calor neto agregado está dado por Q add, ex = H 3 – H 2 [kJ] o Q add = C p . (T 3 -T 2s ) , pero en este caso no sabemos La temperatura (T 2s ) en la salida del compresor. Resolveremos este problema en variables intensivas . Tenemos que reescribir la ecuación anterior (para incluir η K ) usando el término ( + h 1 – h 1 ) para:
Q add = h 3 – h 2 = h 3 – h 1 – (h 2s – h 1 ) / η K [kJ / kg]
Q add = c p (T 3 -T 1 ) – (c p (T 2s -T 1 ) / η K )
Luego calcularemos la temperatura, T 2s , utilizando la relación p, V, T (de la Ley de gases ideales ) para el proceso adiabático entre (1 → 2).
En esta ecuación, el factor para helio es igual a = c p / c v = 1.66. De la ecuación anterior se deduce que la temperatura de salida del compresor, T 2s , es:
Q add = c p (T 3 -T 1 ) – (c p (T 2s -T 1 ) / η K ) = 5200. (1190 – 299) – 5200. (424-299) /0.87 = 4.633 MJ / kg – 0.747 MJ / kg = 3.886 MJ / kg
3)
El trabajo realizado en el gas por el compresor en el proceso de compresión isentrópica es:
W C, s = c p (T 2s – T 1 ) = 5200 x (424 – 299) = 0.650 MJ / kg
El verdadero trabajo realizado en el gas por el compresor en la compresión adiabática es entonces:
W C, real = c p (T 2s – T 1 ). η C = 5200 x (424 – 299) / 0.87 = 0.747 MJ / kg
4)
La temperatura de salida de la turbina del gas, T 4, se puede calcular utilizando la misma relación p, V, T que en 2) pero entre los estados 3 y 4:
De la ecuación anterior se deduce que la temperatura de salida del gas, T 4 , es:
5)
El trabajo realizado por la turbina de gas en la expansión isentrópica es entonces:
W T, s = c p (T 3 – T 4s ) = 5200 x (1190 – 839) = 1.825 MJ / kg
El verdadero trabajo realizado por la turbina de gas en la expansión adiabática es entonces:
W T, real = c p (T 3 – T 4s ). η T = 5200 x (1190 – 839) x 0.91 = 1.661 MJ / kg
6)
Como se dedujo en la sección anterior, la eficiencia térmica de un ciclo Brayton ideal es una función de la relación de presión y κ :
por lo tanto
η th = 0.295 = 29.5%
La eficiencia térmica también se puede calcular utilizando el trabajo y el calor (sin η K ):
η th, s = ( W T, s – W C, s ) / Q add, s = (1.825 – 0.650) / 3.983 = 0.295 = 29.5%
Finalmente, la eficiencia térmica que incluye la eficiencia de la turbina isentrópica / compresor es:
η th, real = ( W T, real – W C, real ) / Q add = (1.661 – 0.747) / 3.886 = 0.235 = 23.5%
……………………………………………………………………………………………………………………………….
Este artículo se basa en la traducción automática del artículo original en inglés. Para más información vea el artículo en inglés. Puedes ayudarnos. Si desea corregir la traducción, envíela a: translations@nuclear-power.com o complete el formulario de traducción en línea. Agradecemos su ayuda, actualizaremos la traducción lo antes posible. Gracias.
