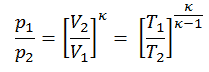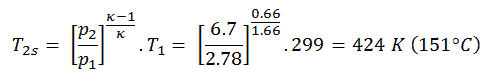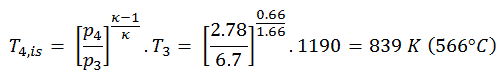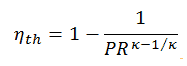Ciclo de Brayton – Problema com a solução
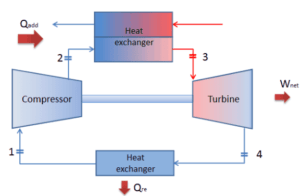Vamos assumir o ciclo fechado de Brayton , que é um dos ciclos termodinâmicos mais comuns encontrados nos modernos motores de turbina a gás. Nesse caso, assuma uma turbina a gás hélio com um único compressor e arranjo de turbina única. Um dos principais parâmetros de tais motores é a temperatura máxima de entrada da turbina e a razão de pressão do compressor (PR = p 2 / p 1 ), que determina a eficiência térmica desse motor.
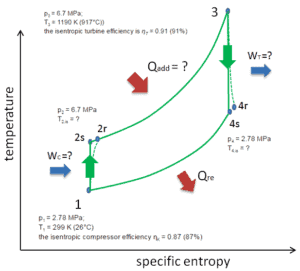
Nesta turbina, o estágio de alta pressão recebe gás (ponto 3 na figura) de um trocador de calor:
- p 3 = 6,7 MPa;
- T 3 = 1190 K (917 ° C))
- a eficiência da turbina isentrópica é η T = 0,91 (91%)
e esvazie-o em outro trocador de calor, onde a pressão de saída é (ponto 4):
- p 4 = 2,78 MPa
- T 4, é =?
Assim, a razão de pressão do compressor é igual a PR = 2,41. Além disso, sabemos que o compressor recebe gás (ponto 1) na figura:
- p 1 = 2,78 MPa;
- T 1 = 299 K (26 ° C)
- a eficiência isentrópica do compressor η K = 0,87 (87%).
A razão de capacidade térmica,, para o hélio é igual a = c p / c v = 1,66
Calcular:
- o calor adicionado pelo trocador de calor (entre 2 → 3)
- a temperatura de saída do compressor do gás (T2 , é )
- o trabalho real realizado neste compressor, quando a eficiência isentrópica do compressor é η K = 0,87 (87%)
- a temperatura de saída da turbina do gás (T 4, é )
- o trabalho real realizado por essa turbina, quando a eficiência da turbina isentrópica é η T = 0,91 (91%)
- a eficiência térmica deste ciclo
Solução:
1) + 2)
A partir da primeira lei da termodinâmica , o calor líquido adicionado é dado por Q add, ex = H 3 – H 2 [kJ] ou Q add = C p . (T 3 -T 2s ) , mas neste caso não sabemos a temperatura (T 2s ) na saída do compressor. Vamos resolver esse problema em variáveis intensivas . Temos que reescrever a equação anterior (para incluir η K ) usando o termo ( + h 1 – h 1 ) para:
Q adicione = h 3 – h 2 = h 3 – h 1 – (h 2 s – h 1 ) / η K [kJ / kg]
Q add = c p (T 3 -T 1 ) – (c p (t 2s -T 1 ) / η K )
Em seguida, iremos calcular a temperatura, T 2s , utilizando p, V, T Relação (a partir de lei do gás ideal ) para processo adiabático entre (1 → 2).
Nesta equação, o fator para o hélio é igual a = c p / c v = 1,66. A partir da equação anterior segue-se que a temperatura de saída do compressor, t 2s , é:
Usando esta temperatura e a eficiência isentrópica do compressor , podemos calcular o calor adicionado pelo trocador de calor:Q add = c p (T 3 -T 1 ) – (c p (t 2s -T 1 ) / η K ) = 5200. (1190 – 299) – 5200. (424-299) /0.87 = 4,633 MJ / kg – 0,747 MJ / kg = 3,886 MJ / kg
3)
O trabalho realizado no gás pelo compressor no processo de compressão isentrópica é:
W C, S = C p (t 2s – T 1 ) = 5200 x (424 – 299) = 0,650 MJ / kg
O trabalho real feito no gás pelo compressor na compressão adiabática é então:
W C, verdadeiro = c p (t 2s – T 1 ). η C = 5200 x (424 – 299) / 0,87 = 0,747 MJ / kg
4)
A temperatura de saída da turbina do gás, T4 , é , pode ser calculada usando a mesma relação p, V, T que em 2), mas entre os estados 3 e 4:
A partir da equação anterior, segue que a temperatura de saída do gás, T 4 , é:
5)
O trabalho realizado pela turbina a gás na expansão isentrópica é então:
W T, s = c p ( T3 – T4s ) = 5200 x (1190 – 839) = 1,825 MJ / kg
O verdadeiro trabalho realizado pela turbina a gás na expansão adiabática é então:
WT , real = cp ( T3 – T4s ). η T = 5200 x (1190 – 839) x 0,91 = 1,661 MJ / kg
6)
Como foi derivado na seção anterior, a eficiência térmica de um ciclo de Brayton ideal é uma função da razão de pressão e κ :
Portanto
η th = 0,295 = 29,5%
A eficiência térmica também pode ser calculada usando o trabalho e o calor (sem η K ):
η th, s = ( WT , s – WC , s ) / adição de Q , s = (1,825 – 0,650) / 3,983 = 0,295 = 29,5%
Finalmente, a eficiência térmica, incluindo a eficiência isentrópica de turbina / compressor, é:
η th, real = ( WT , real – WC , real ) / Q add = (1,661 – 0,747) / 3,886 = 0,235 = 23,5%
……………………………………………………………………………………………………………………………….
Este artigo é baseado na tradução automática do artigo original em inglês. Para mais informações, consulte o artigo em inglês. Você pode nos ajudar. Se você deseja corrigir a tradução, envie-a para: translations@nuclear-power.com ou preencha o formulário de tradução on-line. Agradecemos sua ajuda, atualizaremos a tradução o mais rápido possível. Obrigado.
