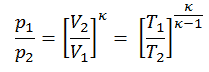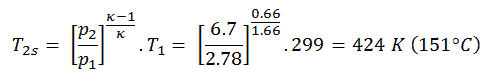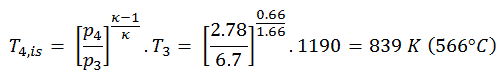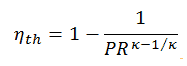Brayton-Zyklus – Problem mit Lösung
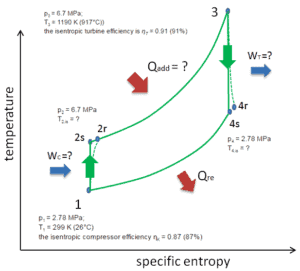
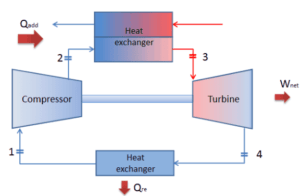Angenommen, der geschlossene Brayton-Zyklus ist einer der häufigsten thermodynamischen Kreisprozessen , die in modernen Gasturbinentriebwerken zu finden sind. In diesem Fall sei eine Heliumgasturbine mit Einzelverdichter und Einzelturbinenanordnung angenommen. Einer der Schlüsselparameter solcher Motoren ist die maximale Turbineneinlasstemperatur und das Kompressordruckverhältnis (PR = p 2 / p 1 ), die den thermischen Wirkungsgrad eines solchen Motors bestimmen.
In dieser Turbine erhält die Hochdruckstufe Gas (Punkt 3 in der Abbildung) von einem Wärmetauscher:
- p 3 = 6,7 MPa;
- T 3 = 1190 K (917 ° C)
- der Wirkungsgrad der isentropen Turbine beträgt η T = 0,91 (91%)
und lasse es zu einem anderen Wärmetauscher ab, wo der Ausgangsdruck ist (Punkt 4):
- p 4 = 2,78 MPa
- T 4 ist =?
Somit ist das Kompressordruckverhältnis gleich PR = 2,41. Außerdem wissen wir, dass der Kompressor in der Abbildung Gas (Punkt 1) erhält:
- p 1 = 2,78 MPa;
- T 1 = 299 K (26 ° C)
- der Wirkungsgrad des isentropischen Kompressors η K = 0,87 (87%).
Das Wärmekapazitätsverhältnis für Helium ist gleich = c p / c v = 1,66
Berechnung:
- die vom Wärmetauscher zugeführte Wärme (zwischen 2 → 3)
- die Kompressorauslasstemperatur des Gases (T 2, ist )
- die eigentliche Arbeit an diesem Kompressor, wenn der Wirkungsgrad des isentropischen Kompressors η K = 0,87 (87%) beträgt
- die Turbinenaustrittstemperatur des Gases (T 4, ist )
- die eigentliche Arbeit dieser Turbine, wenn der Wirkungsgrad der isentropischen Turbine η T = 0,91 (91%) beträgt
- der thermische Wirkungsgrad dieses Zyklus
Lösung:
1) + 2)
Nach dem ersten Hauptsatz der Thermodynamik ist die hinzugefügte Nettowärme gegeben durch Q add, ex = H 3 – H 2 [kJ] oder Q add = C p (T 3 -T 2s ) , aber in diesem Fall wissen wir es nicht die Temperatur (T 2s ) am Auslass des Kompressors. Wir werden dieses Problem in intensiven Variablen lösen . Wir müssen die vorherige Gleichung (um η K einzuschließen ) unter Verwendung des Terms ( + h 1 – h 1 ) umschreiben, um:
Q add = h 3 – h 2 = h 3 – h 1 – (h 2s – h 1 ) / η K [kJ / kg]
Q addiere = c p (T 3 -T 1 ) – (c p (T 2s -T 1 ) / η K )
Dann berechnen wir die Temperatur T 2s unter Verwendung der p, V, T-Beziehung (aus dem idealen Gasgesetz ) für den adiabatischen Prozess zwischen (1 → 2).
In dieser Gleichung ist der Faktor für Helium gleich = c p / c v = 1,66. Aus der vorherigen Gleichung folgt, dass die Kompressorauslasstemperatur T 2s ist:
Mit dieser Temperatur und dem Wirkungsgrad des isentropischen Kompressors können wir die vom Wärmetauscher zugeführte Wärme berechnen:Q add = c p (T 3 -T 1 ) – (c p (T 2s -T 1 ) / η K ) = 5200. (1190 – 299) – 5200. (424-299) / 0,87 = 4,633 MJ / kg – 0,747 MJ / kg = 3,886 MJ / kg
3)
Die Arbeit des Kompressors am Gas im isentropischen Kompressionsprozess ist:
W C, s = c p (T 2s – T 1 ) = 5200 × (424 – 299) = 0,650 MJ / kg
Die eigentliche Arbeit, die der Kompressor bei der adiabatischen Kompression am Gas leistet, ist dann:
W C, real = c p (T 2s – T 1 ). η C = 5200 x (424 – 299) / 0,87 = 0,747 MJ / kg
4)
Die Turbinenauslasstemperatur des Gases T 4 kann unter Verwendung der gleichen p, V, T-Beziehung wie in 2) berechnet werden , jedoch zwischen den Zuständen 3 und 4:
Aus der vorhergehenden Gleichung folgt, dass die Austrittstemperatur des Gases T 4 ist:
5)
Die Arbeit der Gasturbine bei der isentropischen Expansion ist dann:
W T, s = c p (T 3 – T 4 s ) = 5200 × (1190–839) = 1,825 MJ / kg
Die eigentliche Arbeit der Gasturbine bei der adiabatischen Expansion ist dann:
W T, real = c p (T 3 – T 4 s ). η T = 5200 x (1190 – 839) x 0,91 = 1,661 MJ / kg
6)
Wie im vorherigen Abschnitt abgeleitet, ist der thermische Wirkungsgrad eines idealen Brayton-Zyklus eine Funktion des Druckverhältnisses und von κ :
deshalb
η th = 0,295 = 29,5%
Der thermische Wirkungsgrad kann auch anhand der Arbeit und der Wärme (ohne η K ) berechnet werden :
η th, s = ( W T, s – W C, s ) / Q add, s = (1,825 – 0,650) / 3,983 = 0,295 = 29,5%
Schließlich beträgt der thermische Wirkungsgrad einschließlich des Wirkungsgrads der isentropischen Turbine / des Kompressors:
η th, real = ( W T, real – W C, real ) / Q add = (1,661 – 0,747) / 3,886 = 0,235 = 23,5%
……………………………………………………………………………………………………………………………….
Dieser Artikel basiert auf der maschinellen Übersetzung des englischen Originalartikels. Weitere Informationen finden Sie im Artikel auf Englisch. Sie können uns helfen. Wenn Sie die Übersetzung korrigieren möchten, senden Sie diese bitte an: translations@nuclear-power.com oder füllen Sie das Online-Übersetzungsformular aus. Wir bedanken uns für Ihre Hilfe und werden die Übersetzung so schnell wie möglich aktualisieren. Danke.
