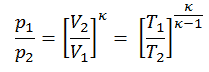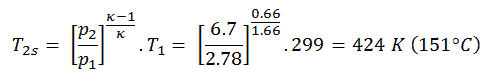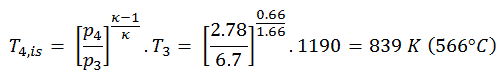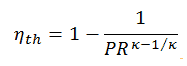Cycle de Brayton – Problème de solution
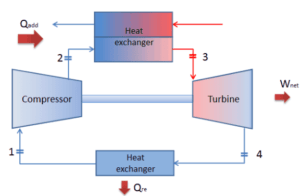Supposons le cycle de Brayton fermé , qui est l’un des cycles thermodynamiques les plus courants que l’on puisse trouver dans les moteurs à turbine à gaz modernes. Dans ce cas, supposons une turbine à gaz à hélium avec un seul compresseur et une seule turbine. L’un des paramètres clés de ces moteurs est la température maximale à l’entrée de la turbine et le taux de compression du compresseur (PR = p 2 / p 1 ), qui détermine l’efficacité thermique de ce moteur.
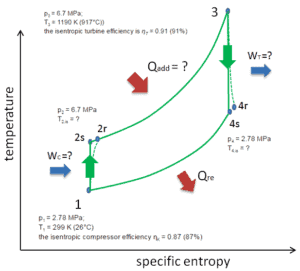
Dans cette turbine, l’étage haute pression reçoit le gaz (point 3 sur la figure) d’un échangeur de chaleur:
- p 3 = 6,7 MPa;
- T 3 = 1190 K (917 ° C))
- le rendement de la turbine isentropique est η T = 0,91 (91%)
et évacuez-le vers un autre échangeur de chaleur, où la pression de sortie est (point 4):
- p 4 = 2,78 MPa
- T 4, est =?
Ainsi, le rapport de pression du compresseur est égal à PR = 2,41. De plus, nous savons que le compresseur reçoit du gaz (point 1) sur la figure:
- p 1 = 2,78 MPa;
- T 1 = 299 K (26 ° C)
- le rendement du compresseur isentropique η K = 0,87 (87%).
Le rapport de capacité thermique,, pour l’hélium est égal à = c p / c v = 1,66
Calculer:
- la chaleur ajoutée par l’échangeur de chaleur (entre 2 → 3)
- la température de sortie du compresseur du gaz (T 2, est )
- le vrai travail effectué sur ce compresseur, lorsque l’efficacité du compresseur isentropique est η K = 0,87 (87%)
- la température de sortie de la turbine du gaz (T 4, est )
- le travail réel effectué par cette turbine, lorsque le rendement de la turbine isentropique est η T = 0,91 (91%)
- l’efficacité thermique de ce cycle
Solution:
1) + 2)
D’après la première loi de la thermodynamique , la chaleur nette ajoutée est donnée par Q add, ex = H 3 – H 2 [kJ] ou Q add = C p . (T 3 -T 2s ) , mais dans ce cas nous ne savons pas la température (T 2s ) à la sortie du compresseur. Nous allons résoudre ce problème en variables intensives . Nous devons réécrire l’équation précédente (pour inclure η K ) en utilisant le terme ( + h 1 – h 1 ) pour:
Q add = h 3 – h 2 = h 3 – h 1 – (h 2s – h 1 ) / η K [kJ / kg]
Q add = c p (T 3 -T 1 ) – (c p (T 2s -T 1 ) / η K )
Ensuite, nous calculerons la température, T 2s , en utilisant la relation p, V, T (de la loi des gaz parfaits ) pour le processus adiabatique entre (1 → 2).
Dans cette équation, le facteur pour l’hélium est égal à = c p / c v = 1,66. D’après l’équation précédente, la température de sortie du compresseur, T 2s , est:
3)
Le travail effectué sur le gaz par le compresseur dans le processus de compression isentropique est:
W C, s = c p (T 2s – T 1 ) = 5200 x (424 – 299) = 0,650 MJ / kg
Le vrai travail effectué sur le gaz par le compresseur dans la compression adiabatique est alors:
W C, réel = c p (T 2s – T 1 ). η C = 5200 x (424 – 299) / 0,87 = 0,747 MJ / kg
4)
La température de sortie de turbine du gaz, T 4, est , peut être calculée en utilisant la même relation p, V, T qu’en 2) mais entre les états 3 et 4:
De l’équation précédente, la température de sortie du gaz, T 4 , est:
5)
Le travail effectué par la turbine à gaz dans l’expansion isentropique est alors:
W T, s = c p (T 3 – T 4s ) = 5200 x (1190 – 839) = 1,825 MJ / kg
Le véritable travail effectué par la turbine à gaz dans l’expansion adiabatique est alors:
W T, réel = c p (T 3 – T 4s ). η T = 5200 x (1190 – 839) x 0,91 = 1,661 MJ / kg
6)
Comme il a été dérivé dans la section précédente, l’ efficacité thermique d’un cycle de Brayton idéal est fonction du rapport de pression et de κ :
par conséquent
η th = 0,295 = 29,5%
L’efficacité thermique peut également être calculée en utilisant le travail et la chaleur (sans η K ):
η th, s = ( W T, s – W C, s ) / Q add, s = (1,825 – 0,650) / 3,998 = 0,295 = 29,5%
Enfin, l’efficacité thermique, y compris l’efficacité turbine / compresseur isentropique, est:
η e, réel = ( W T, réel – W C, réel ) / Q add = (1,661 – 0,747) / 3,886 = 0,235 = 23,5%
……………………………………………………………………………………………………………………………….
Cet article est basé sur la traduction automatique de l’article original en anglais. Pour plus d’informations, voir l’article en anglais. Pouvez vous nous aider Si vous souhaitez corriger la traduction, envoyez-la à l’adresse: translations@nuclear-power.com ou remplissez le formulaire de traduction en ligne. Nous apprécions votre aide, nous mettrons à jour la traduction le plus rapidement possible. Merci
