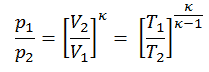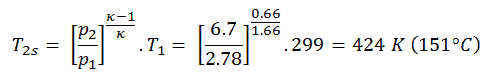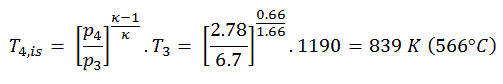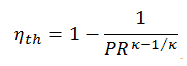What is Example of Brayton Cycle – Problem with Solution

Example of Brayton Cycle – Problem with Solution. Calculate for the closed Brayton cycle key thermodynamic parameters such as temperatures, pressures and heat transfers. Thermal Engineering

Brayton Cycle – Problem with Solution

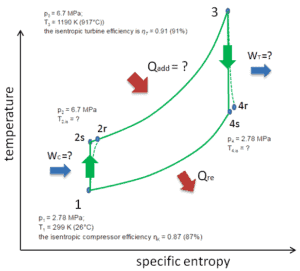
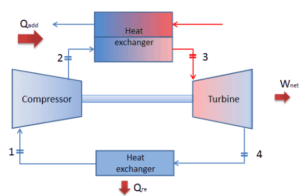Let assume the closed Brayton cycle, which is the one of most common thermodynamic cycles that can be found in modern gas turbine engines. In this case assume a helium gas turbine with single compressor and single turbine arrangement. One of key parameters of such engines is the maximum turbine inlet temperature and the compressor pressure ratio (PR = p₂/p₁) which determines the thermal efficiency of such engine.

In this turbine the high-pressure stage receives gas (point 3 at the figure) from a heat exchanger:

p₃= 6.7 MPa;
T₃ = 1190 K (917°C))
the isentropic turbine efficiency is η_T = 0.91 (91%)

and exhaust it to another heat exchanger, where the outlet pressure is (point 4):

p₄ = 2.78 MPa
T_4,is = ?

Thus the compressor pressure ratio is equal to PR = 2.41. Moreover we know, that the compressor receives gas (point 1) at the figure:

p₁= 2.78 MPa;
T₁ = 299 K (26°C)
the isentropic compressor efficiency η_K = 0.87 (87%).

The heat capacity ratio, , for helium is equal to =c_p/c_v=1.66

Calculate:

the heat added by the heat exchanger (between 2 → 3)
the compressor outlet temperature of the gas (T_2,is)
the real work done on this compressor, when the isentropic compressor efficiency is η_K = 0.87 (87%)
the turbine outlet temperature of the gas (T_4,is)
the real work done by this turbine, when the isentropic turbine efficiency is η_T = 0.91 (91%)
the thermal efficiency of this cycle

Solution:

1) + 2)

From the first law of thermodynamics, the net heat added is given by Q_add,ex = H₃– H₂ [kJ] or Q_add = C_p.(T₃-T_2s), but in this case we do not know the temperature (T_2s) at the outlet of the compressor. We will solve this problem in intensive variables. We have to rewrite the previous equation (to include η_K) using the term (+h₁ – h₁) to:

Q_add = h₃ – h₂ = h₃ – h₁ – (h_2s – h₁)/η_K [kJ/kg]

Q_add= c_p(T₃-T₁) – (c_p(T_2s-T₁)/η_K)

Then we will calculate the temperature, T_2s, using p, V, T Relation (from Ideal Gas Law) for adiabatic process between (1 → 2).

In this equation the factor for helium is equal to =c_p/c_v=1.66. From the previous equation follows that the compressor outlet temperature, T_2s, is:

Specific Heat Calculation

From Ideal Gas Law we know, that the molar specific heat of a monatomic ideal gas is:

C_v = 3/2R = 12.5 J/mol K and C_p = C_v + R = 5/2R = 20.8 J/mol K

We transfer the specific heat capacities into units of J/kg K via:

c_p = C_p . 1/M (molar weight of helium) = 20.8 x 4.10^-3 = 5200 J/kg K

Using this temperature and the isentropic compressor efficiency we can calculate the heat added by the heat exchanger:

Q_add= c_p(T₃-T₁) – (c_p(T_2s-T₁)/η_K) = 5200.(1190 – 299) – 5200.(424-299)/0.87 = 4.633 MJ/kg – 0.747 MJ/kg = 3.886 MJ/kg

The work done on the gas by the compressor in the isentropic compression process is:

W_C,s = c_p (T_2s – T₁) = 5200 x (424 – 299) = 0.650 MJ/kg

The real work done on the gas by the compressor in the adiabatic compression is then:

W_C,real = c_p (T_2s – T₁). η_C = 5200 x (424 – 299) / 0.87 = 0.747 MJ/kg

The turbine outlet temperature of the gas, T_4,is, can be calculated using the same p, V, T Relation as in 2) but between states 3 and 4:

From the previous equation follows that the outlet temperature of the gas, T_4,is, is:

The work done by gas turbine in the isentropic expansion is then:

W_T,s = c_p (T₃ – T_4s) = 5200 x (1190 – 839) = 1.825 MJ/kg

The real work done by gas turbine in the adiabatic expansion is then:

W_T,real = c_p (T₃ – T_4s) . η_T = 5200 x (1190 – 839) x 0.91 = 1.661 MJ/kg

As was derived in the previous section, the thermal efficiency of an ideal Brayton cycle is a function of pressure ratio and κ:

therefore

η_th= 0.295 = 29.5%

The thermal efficiency can be also calculated using the work and the heat (without η_K):

η_th,s= (W_T,s – W_C,s) / Q_add,s = (1.825 – 0.650) / 3.983 = 0.295 = 29.5%

Finally, the thermal efficiency including isentropic turbine/compressor efficiency is:

η_th,real= (W_T,real – W_C,real) / Q_add = (1.661 – 0.747) / 3.886 = 0.235 = 23.5%

References:

Nuclear and Reactor Physics:

J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
W.S.C. Williams. Nuclear and Particle Physics. Clarendon Press; 1 edition, 1991, ISBN: 978-0198520467
Kenneth S. Krane. Introductory Nuclear Physics, 3rd Edition, Wiley, 1987, ISBN: 978-0471805533
G.R.Keepin. Physics of Nuclear Kinetics. Addison-Wesley Pub. Co; 1st edition, 1965
Robert Reed Burn, Introduction to Nuclear Reactor Operation, 1988.
U.S. Department of Energy, Nuclear Physics and Reactor Theory. DOE Fundamentals Handbook, Volume 1 and 2. January 1993.

Advanced Reactor Physics:

K. O. Ott, W. A. Bezella, Introductory Nuclear Reactor Statics, American Nuclear Society, Revised edition (1989), 1989, ISBN: 0-894-48033-2.
K. O. Ott, R. J. Neuhold, Introductory Nuclear Reactor Dynamics, American Nuclear Society, 1985, ISBN: 0-894-48029-4.
D. L. Hetrick, Dynamics of Nuclear Reactors, American Nuclear Society, 1993, ISBN: 0-894-48453-2.
E. E. Lewis, W. F. Miller, Computational Methods of Neutron Transport, American Nuclear Society, 1993, ISBN: 0-894-48452-4.

Other References:

Diesel Engine – Car Recycling

What is Example of Brayton Cycle – Problem with Solution – Definition

Brayton Cycle – Problem with Solution

See also:

Brayton Cycle – Problem with Solution

See also:

Related Posts