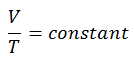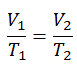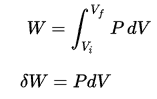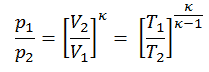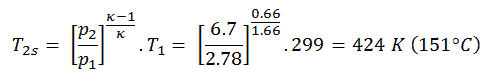Proceso isobárico
Un proceso isobárico es un proceso termodinámico , en el cual la presión del sistema permanece constante (p = const). La transferencia de calor dentro o fuera del sistema funciona, pero también cambia la energía interna del sistema.
Dado que hay cambios en la energía interna (dU) y cambios en el volumen del sistema (∆V), los ingenieros a menudo usan la entalpía del sistema, que se define como:
H = U + pV
En muchos análisis termodinámicos es conveniente utilizar la entalpía en lugar de la energía interna. Especialmente en el caso de la primera ley de la termodinámica .
La entalpía es la expresión preferida de la energía del sistema que cambia en muchas mediciones químicas, biológicas y físicas a presión constante . Es tan útil que está tabulado en las tablas de vapor junto con un volumen específico y una energía interna específica . Es debido al hecho, simplifica la descripción de la transferencia de energía . A presión constante, el cambio de entalpía es igual a la energía transferida desde el medio ambiente a través del calentamiento (Q = H 2 – H 1 ) u otro trabajo que no sea el trabajo de expansión. Para un proceso de presión variable, la diferencia en entalpía no es tan obvia.
Hay expresiones en términos de variables más familiares como temperatura y presión :
dH = C p dT + V (1-αT) dp
Donde C p es la capacidad calorífica a presión constante y α es el coeficiente de expansión térmica (cúbica). Para gas ideal αT = 1 y por lo tanto:
dH = C p dT
Para un proceso ideal de gas y politrópico, el caso n = 0 corresponde a un proceso isobárico (presión constante). A diferencia del proceso adiabático, en el que n = y un sistema no intercambia calor con su entorno (Q = 0; ∆T ≠ 0 ) , en un proceso isobárico hay un cambio en la energía interna (debido a ∆T ≠ 0) y por lo tanto ΔU ≠ 0 (para gases ideales) y Q ≠ 0.
En ingeniería, ambos ciclos termodinámicos muy importantes (ciclo de Brayton y Rankine ) se basan en dos procesos isobáricos, por lo tanto, el estudio de este proceso es crucial para las centrales eléctricas.
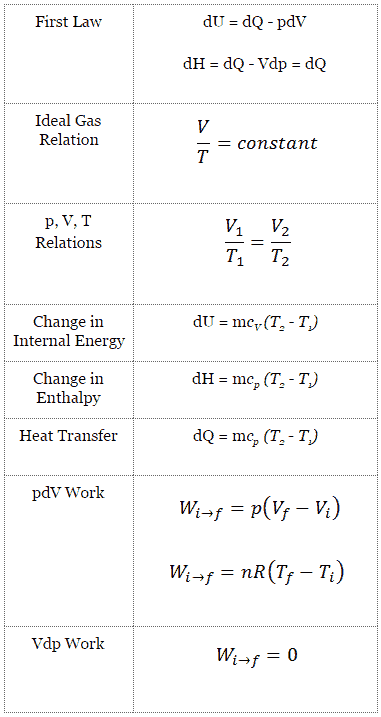
Proceso isobárico y la primera ley
La forma clásica de la primera ley de la termodinámica es la siguiente ecuación:
dU = dQ – dW
En esta ecuación, dW es igual a dW = pdV y se conoce como el trabajo límite .
En un proceso isobárico y el gas ideal, parte del calor agregado al sistema se utilizará para hacer el trabajo y parte del calor agregado aumentará la energía interna (aumentará la temperatura). Por lo tanto, es conveniente utilizar la entalpía en lugar de la energía interna. Dado que H = U + pV , entonces dH = dU + pdV + Vdp y sustituimos dU = dH – pdV – Vdp en la forma clásica de la ley:
dH – pdV – Vdp = dQ – pdV
Obtenemos la ley en términos de entalpía :
dH = dQ + Vdp
o
dH = TdS + Vdp
En esta ecuación, el término Vdp es un proceso de flujo de trabajo. Este trabajo, Vdp , se utiliza para sistemas de flujo abierto como una turbina o una bomba en la que hay un “dp” , es decir, un cambio de presión. No hay cambios en el volumen de control . Como puede verse, esta forma de ley simplifica la descripción de la transferencia de energía . A presión constante , el cambio de entalpía es igual a la energía transferida del ambiente a través del calentamiento:
Proceso isobárico (Vdp = 0):
dH = dQ → Q = H 2 – H 1
En una entropía constante , es decir, en un proceso isentrópico, el cambio de entalpía equivale al trabajo del proceso de flujo realizado en o por el sistema.
Proceso isentrópico (dQ = 0):
dH = Vdp → W = H 2 – H 1
Es obvio, será muy útil en el análisis de los dos ciclos termodinámicos utilizados en la ingeniería de potencia, es decir, en el ciclo Brayton y el ciclo Rankine.
Proceso isobárico: ecuación de gas ideal
Ver también: ¿Qué es un gas ideal?
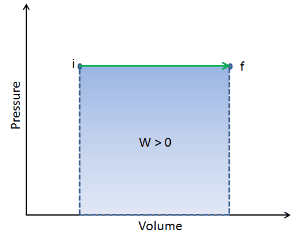
Supongamos una adición de calor isobárico en un gas ideal. En un gas ideal , las moléculas no tienen volumen y no interactúan. Según la ley de los gases ideales , la presión varía linealmente con la temperatura y la cantidad, e inversamente con el volumen .
pV = nRT
dónde:
- p es la presión absoluta del gas
- n es la cantidad de sustancia
- T es la temperatura absoluta
- V es el volumen
- R es la constante de gas ideal, o universal, igual al producto de la constante de Boltzmann y la constante de Avogadro,
En esta ecuación, el símbolo R es una constante llamada constante de gas universal que tiene el mismo valor para todos los gases, es decir, R = 8.31 J / mol K.
El proceso isobárico se puede expresar con la ley de los gases ideales como:
o
En un diagrama pV , el proceso ocurre a lo largo de una línea horizontal (llamada isobar) que tiene la ecuación p = constante.
El trabajo de presión-volumen del sistema cerrado se define como:
Suponiendo que la cantidad de gas ideal permanece constante y aplicando la ley del gas ideal , esto se convierte en
Según el modelo de gas ideal, la energía interna se puede calcular mediante:
∆U = mc v ∆T
donde la propiedad c v (J / mol K) se denomina calor específico (o capacidad calorífica ) a un volumen constante porque, bajo ciertas condiciones especiales (volumen constante), relaciona el cambio de temperatura de un sistema con la cantidad de energía agregada por transferencia de calor.
Al sumar estas ecuaciones, obtenemos la ecuación para el calor:
Q = mc v ∆T + m R ∆T = m (c v + R) ∆T = m c p ∆T
donde la propiedad c p (J / mol K) se denomina calor específico (o capacidad calorífica ) a una presión constante.
Ver también: Calor específico a volumen constante y presión constante
Ver también: fórmula de Mayer
Ley de carlos
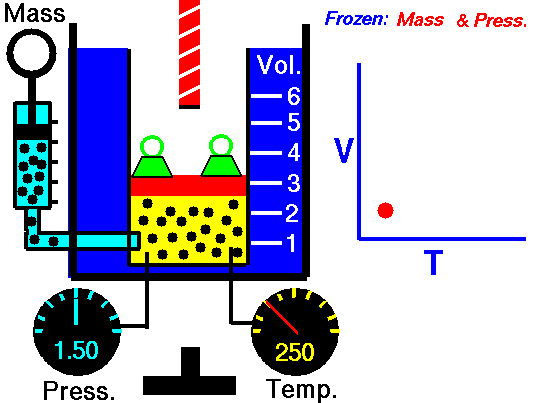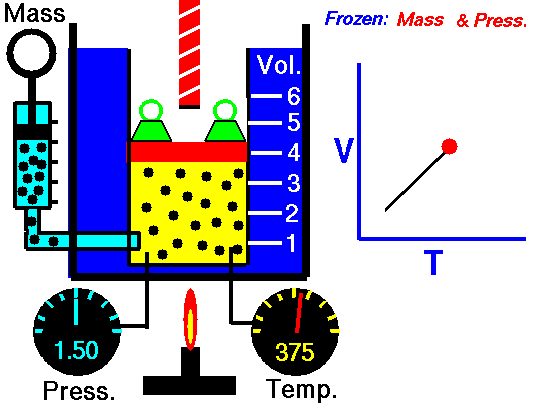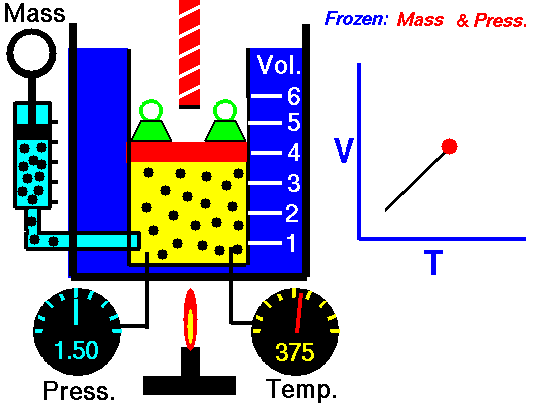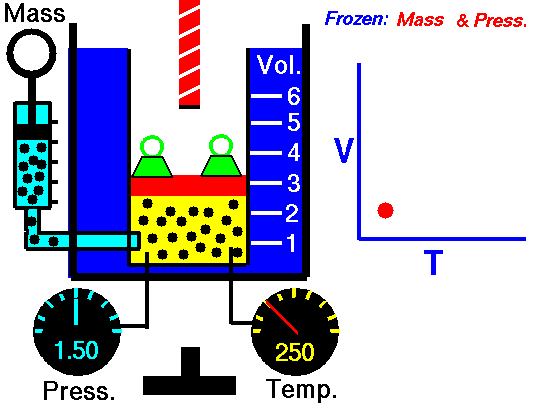
La Ley de Charles es una de las leyes del gas. A finales del siglo XVIII, el inventor y científico francés Jacques Alexandre César Charles estudió la relación entre el volumen y la temperatura de un gas a presión constante . Los resultados de ciertos experimentos con gases a una presión relativamente baja llevaron a Jacques Alexandre César Charles a formular una ley bien conocida. Se afirma que:
Para una masa fija de gas a presión constante, el volumen es directamente proporcional a la temperatura Kelvin.
Eso significa que, por ejemplo, si duplica la temperatura, duplicará el volumen. Si reduce a la mitad la temperatura, reducirá a la mitad el volumen.
Puede expresar esto matemáticamente como:
V = constante. T
Sí, parece ser idéntico al proceso isobárico del gas ideal. Estos resultados son totalmente consistentes con la ley del gas ideal , que determina que la constante es igual a nR / p . Si reorganiza la ecuación pV = nRT dividiendo ambos lados por p, obtendrá:
V = nR / p. T
donde nR / p es constante y:
- p es la presión absoluta del gas
- n es la cantidad de sustancia
- T es la temperatura absoluta
- V es el volumen
- R es la constante de gas ideal, o universal, igual al producto de la constante de Boltzmann y la constante de Avogadro,
En esta ecuación, el símbolo R es una constante llamada constante de gas universal que tiene el mismo valor para todos los gases, es decir, R = 8.31 J / mol K.
Ejemplo de proceso isobárico: adición de calor isobárico

Supongamos el ciclo Brayton ideal que describe el funcionamiento de un motor de calor a presión constante . Los modernos motores de turbina de gas y los motores de inyección de aire también siguen el ciclo Brayton.
El ciclo ideal de Brayton consiste en cuatro procesos termodinámicos. Dos procesos isentrópicos y dos procesos isobáricos.
- Compresión isentrópica : el aire ambiente ingresa al compresor, donde se presuriza (1 → 2). El trabajo requerido para el compresor viene dado por W C = H 2 – H 1 .
- adición de calor isobárico : el aire comprimido pasa a través de una cámara de combustión, donde se quema el combustible y se calienta el aire u otro medio (2 → 3). Es un proceso de presión constante, ya que la cámara está abierta para fluir hacia adentro y hacia afuera. El calor neto agregado viene dado por Q add = H 3 – H 2
- Expansión isentrópica : el aire calentado y presurizado se expande en la turbina y abandona su energía. El trabajo realizado por la turbina viene dado por W T = H 4 – H 3
- rechazo de calor isobárico : el calor residual debe rechazarse para cerrar el ciclo. El calor neto rechazado viene dado por Q re = H 4 – H 1
Suponga una adición de calor isobárico (2 → 3) en un intercambiador de calor. En las turbinas de gas típicas, la etapa de alta presión recibe gas (punto 3 en la figura; p 3 = 6,7 MPa ; T 3 = 1190 K (917 ° C)) de un intercambiador de calor. Además, sabemos que el compresor recibe gas (punto 1 en la figura; p 1 = 2.78 MPa ; T 1 = 299 K (26 ° C)) y sabemos que la eficiencia isentrópica del compresor es η K = 0.87 (87 %) .
Calcule el calor agregado por el intercambiador de calor (entre 2 → 3).
Solución:
A partir de la primera ley de la termodinámica , el calor neto agregado viene dado por Q add = H 3 – H 2 o Q add = C p . (T 3 -T 2s ), pero en este caso no sabemos la temperatura (T 2s ) a la salida del compresor. Resolveremos este problema en variables intensivas. Tenemos que reescribir la ecuación anterior (para incluir η K ) usando el término (+ h 1 – h 1 ) para:
Q add = h 3 – h 2 = h 3 – h 1 – (h 2s – h 1 ) / η K
Q add = c p (T 3 -T 1 ) – (c p (T 2s -T 1 ) / η K )
Luego calcularemos la temperatura, T 2s , usando p, V, T Relación para el proceso adiabático entre (1 → 2).
En esta ecuación, el factor para helio es igual a = c p / c v = 1.66 . De la ecuación anterior se deduce que la temperatura de salida del compresor, T 2s , es:
Según la Ley del Gas Ideal , sabemos que el calor específico molar de un gas ideal monoatómico es:
C v = 3 / 2R = 12.5 J / mol K y C p = C v + R = 5 / 2R = 20.8 J / mol K
Transferimos las capacidades de calor específicas en unidades de J / kg K a través de:
c p = C p . 1 / M (peso molar de helio) = 20.8 x 4.10 -3 = 5200 J / kg K
Usando esta temperatura y la eficiencia del compresor isentrópico , podemos calcular el calor agregado por el intercambiador de calor:
Q add = c p (T 3 -T 1 ) – (c p (T 2s -T 1 ) / η K ) = 5200. (1190 – 299) – 5200. (424-299) /0.87 = 4.633 MJ / kg – 0.747 MJ / kg = 3.886 MJ / kg