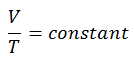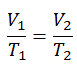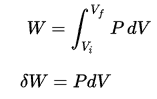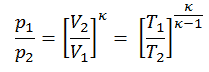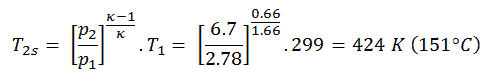Processus isobare
Un processus isobare est un processus thermodynamique , dans lequel la pression du système reste constante (p = const). Le transfert de chaleur dans ou hors du système fonctionne, mais modifie également l’énergie interne du système.
Puisqu’il y a des changements d’ énergie interne (dU) et des changements de volume du système (∆V), les ingénieurs utilisent souvent l’ enthalpie du système, qui est définie comme:
H = U + pV
Dans de nombreuses analyses thermodynamiques, il est commode d’utiliser l’ enthalpie au lieu de l’énergie interne. Surtout dans le cas de la première loi de la thermodynamique .
L’enthalpie est l’expression préférée de l’énergie du système qui change dans de nombreuses mesures chimiques, biologiques et physiques à pression constante . Il est si utile qu’il est tabulé dans les tables de vapeur avec un volume spécifique et une énergie interne spécifique . C’est dû au fait, cela simplifie la description du transfert d’énergie . À pression constante, le changement d’enthalpie est égal à l’énergie transférée de l’environnement par le chauffage (Q = H 2 – H 1 ) ou un travail autre que le travail d’expansion. Pour un procédé à pression variable, la différence d’enthalpie n’est pas aussi évidente.
Il existe des expressions en termes de variables plus familières telles que la température et la pression :
dH = C p dT + V (1-αT) dp
Où C p est la capacité thermique à pression constante et α est le coefficient de dilatation thermique (cubique). Pour un gaz parfait αT = 1 et donc:
dH = C p dT
Pour un gaz parfait et un procédé polytropique, le cas n = 0 correspond à un procédé isobare (pression constante). Contrairement au processus adiabatique, dans lequel n = et un système n’échange pas de chaleur avec son environnement (Q = 0; ∆T ≠ 0 ) , dans un processus isobare, il y a un changement dans l’énergie interne (due à ∆T ≠ 0) et donc ΔU ≠ 0 (pour les gaz parfaits) et Q ≠ 0.
En ingénierie, les deux cycles thermodynamiques très importants (cycle de Brayton et cycle de Rankine ) sont basés sur deux processus isobares, donc l’étude de ce processus est cruciale pour les centrales électriques.
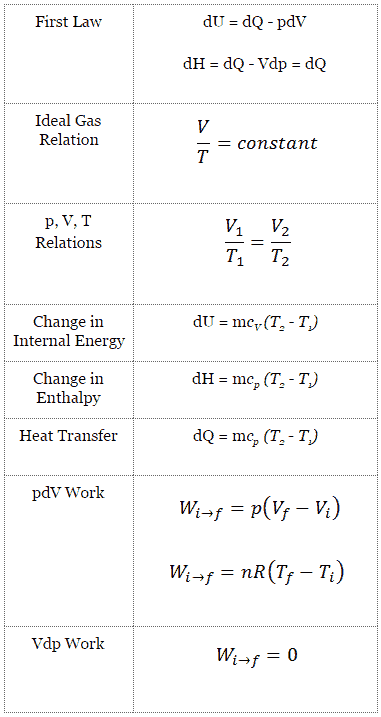
Processus isobare et première loi
La forme classique de la première loi de la thermodynamique est l’équation suivante:
dU = dQ – dW
Dans cette équation, dW est égal à dW = pdV et est connu comme le travail aux limites .
Dans un procédé isobare et le gaz parfait, une partie de la chaleur ajoutée au système sera utilisée pour faire le travail et une partie de la chaleur ajoutée augmentera l’ énergie interne (augmentera la température). Par conséquent, il est commode d’utiliser l’ enthalpie au lieu de l’énergie interne.Depuis H = U + pV , donc dH = dU + pdV + Vdp et nous substituons dU = dH – pdV – Vdp dans la forme classique de la loi:
dH – pdV – Vdp = dQ – pdV
Nous obtenons la loi en matière d’enthalpie :
dH = dQ + Vdp
ou
dH = TdS + Vdp
Dans cette équation, le terme Vdp est un travail de processus d’écoulement. Ce travail, Vdp , est utilisé pour des systèmes à flux ouvert comme une turbine ou une pompe dans lesquels il y a un «dp» , c’est-à-dire un changement de pression. Il n’y a aucun changement dans le volume de contrôle . Comme on peut le voir, cette forme de loi simplifie la description du transfert d’énergie . À pression constante , le changement d’enthalpie est égal à l’ énergie transférée de l’environnement par le chauffage:
Processus isobare (Vdp = 0):
dH = dQ → Q = H 2 – H 1
À entropie constante , c’est-à-dire dans un processus isentropique, le changement d’enthalpie est égal au travail de processus d’écoulement effectué sur ou par le système.
Processus isentropique (dQ = 0):
dH = Vdp → W = H 2 – H 1
Il est évident, il sera très utile dans l’analyse des deux cycles thermodynamiques utilisés en génie énergétique, c’est-à-dire dans le cycle de Brayton et le cycle de Rankine.
Processus isobare – Équation du gaz parfait
Voir aussi: Qu’est-ce qu’un gaz parfait
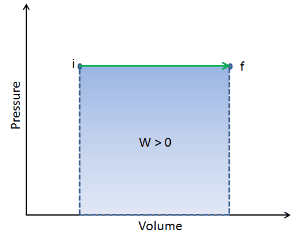
Supposons un apport de chaleur isobare dans un gaz parfait. Dans un gaz parfait , les molécules n’ont pas de volume et n’interagissent pas. Selon la loi du gaz parfait , la pression varie linéairement avec la température et la quantité, et inversement avec le volume .
pV = nRT
où:
- p est la pression absolue du gaz
- n est la quantité de substance
- T est la température absolue
- V est le volume
- R est la constante de gaz parfaite ou universelle, égale au produit de la constante de Boltzmann et de la constante d’Avogadro,
Dans cette équation, le symbole R est une constante appelée constante de gaz universelle qui a la même valeur pour tous les gaz, à savoir R = 8,31 J / mol K.
Le processus isobare peut s’exprimer avec la loi du gaz parfait comme:
ou
Sur un diagramme pV , le processus se produit le long d’une ligne horizontale (appelée isobare) qui a l’équation p = constante.
Le travail pression-volume par le système fermé est défini comme:
En supposant que la quantité de gaz parfait reste constante et en appliquant la loi du gaz parfait , cela devient
Selon le modèle de gaz parfait, l’ énergie interne peut être calculée par:
∆U = mc v ∆T
lorsque la propriété c v (J / mol K) est appelée chaleur spécifique (ou capacité calorifique ) à volume constant car, dans certaines conditions spéciales (volume constant), elle relie le changement de température d’un système à la quantité d’énergie ajoutée par transfert de chaleur.
En additionnant ces équations, nous obtenons l’équation de la chaleur:
Q = mc v ∆T + m R ∆T = m (c v + R) ∆T = m c p ∆T
où la propriété c p (J / mol K) est appelée chaleur spécifique (ou capacité thermique ) à pression constante.
Voir aussi: Chaleur spécifique à volume constant et pression constante
Voir aussi: formule de Mayer
La loi de Charles
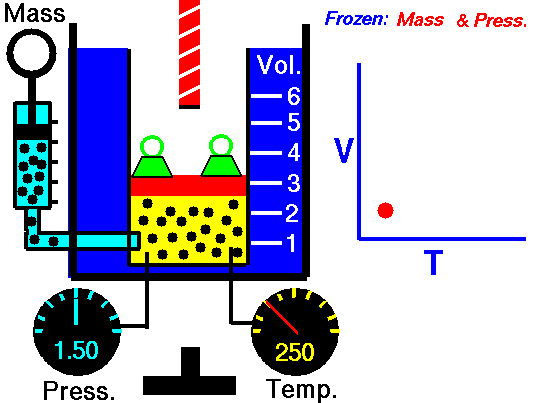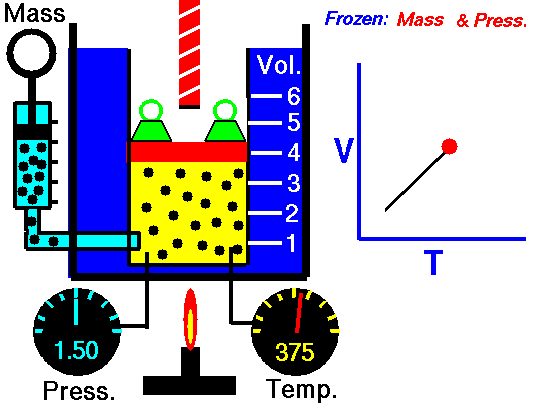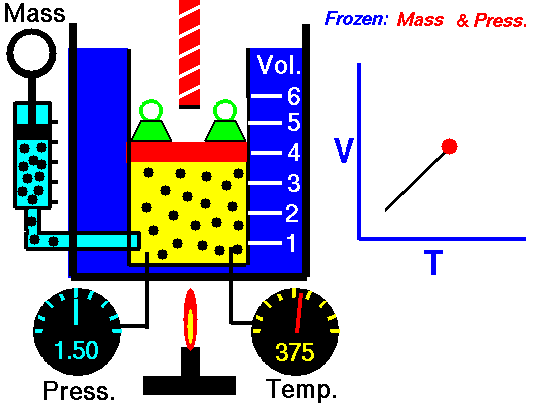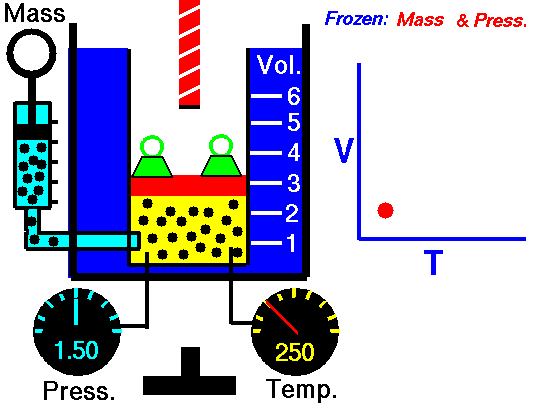
La loi de Charles est l’une des lois sur le gaz. À la fin du XVIIIe siècle, un inventeur et scientifique français Jacques Alexandre César Charles étudie la relation entre le volume et la température d’un gaz à pression constante . Les résultats de certaines expériences avec des gaz à relativement basse pression ont conduit Jacques Alexandre César Charles à formuler une loi bien connue. Il déclare que:
Pour une masse fixe de gaz à pression constante, le volume est directement proportionnel à la température Kelvin.
Cela signifie que, par exemple, si vous doublez la température, vous doublerez le volume. Si vous divisez par deux la température, vous réduisez de moitié le volume.
Vous pouvez exprimer cela mathématiquement comme:
V = constant. T
Oui, il semble être identique au processus isobare du gaz parfait. Ces résultats sont parfaitement cohérents avec la loi du gaz parfait , qui détermine que la constante est égale à nR / p . Si vous réorganisez l’équation pV = nRT en divisant les deux côtés par p, vous obtiendrez:
V = nR / p. T
où nR / p est constant et:
- p est la pression absolue du gaz
- n est la quantité de substance
- T est la température absolue
- V est le volume
- R est la constante de gaz parfaite ou universelle, égale au produit de la constante de Boltzmann et de la constante d’Avogadro,
Dans cette équation, le symbole R est une constante appelée constante de gaz universelle qui a la même valeur pour tous les gaz, à savoir R = 8,31 J / mol K.
Exemple de processus isobare – Addition de chaleur isobare

Supposons le cycle de Brayton idéal qui décrit le fonctionnement d’un moteur thermique à pression constante . Les moteurs à turbine à gaz modernes et les moteurs à réaction à respiration aérienne suivent également le cycle de Brayton.
Le cycle de Brayton idéal se compose de quatre processus thermodynamiques. Deux processus isentropiques et deux processus isobares.
- compression isentropique – l’air ambiant est aspiré dans le compresseur, où il est mis sous pression (1 → 2). Le travail requis pour le compresseur est donné par W C = H 2 – H 1 .
- addition de chaleur isobare – l’air comprimé traverse ensuite une chambre de combustion, où le carburant est brûlé et l’air ou un autre milieu est chauffé (2 → 3). Il s’agit d’un processus à pression constante, car la chambre est ouverte pour entrer et sortir. La chaleur nette ajoutée est donnée par Q add = H 3 – H 2
- expansion isentropique – l’air chauffé sous pression se détend ensuite sur la turbine, cède son énergie. Le travail effectué par turbine est donné par W T = H 4 – H 3
- rejet de chaleur isobare – la chaleur résiduelle doit être rejetée afin de fermer le cycle. La chaleur nette rejetée est donnée par Q re = H 4 – H 1
Supposons un apport de chaleur isobare (2 → 3) dans un échangeur de chaleur. Dans les turbines à gaz typiques, l’étage haute pression reçoit du gaz (point 3 sur la figure; p 3 = 6,7 MPa ; T 3 = 1190 K (917 ° C)) d’un échangeur de chaleur. De plus, nous savons que le compresseur reçoit du gaz (point 1 sur la figure; p 1 = 2,78 MPa ; T 1 = 299 K (26 ° C)) et nous savons que l’efficacité isentropique du compresseur est η K = 0,87 (87 %) .
Calculez la chaleur ajoutée par l’échangeur de chaleur (entre 2 → 3).
Solution:
D’après la première loi de la thermodynamique , la chaleur nette ajoutée est donnée par Q add = H 3 – H 2 ou Q add = C p . (T 3 -T 2s ), mais dans ce cas, nous ne connaissons pas la température (T 2s ) à la sortie du compresseur. Nous allons résoudre ce problème en variables intensives. Nous devons réécrire l’équation précédente (pour inclure η K ) en utilisant le terme (+ h 1 – h 1 ) pour:
Q add = h 3 – h 2 = h 3 – h 1 – (h 2s – h 1 ) / η K
Q add = c p (T 3 -T 1 ) – (c p (T 2s -T 1 ) / η K )
Ensuite, nous calculerons la température, T 2s , en utilisant la relation p, V, T pour le processus adiabatique entre (1 → 2).
Dans cette équation, le facteur pour l’hélium est égal à = c p / c v = 1,66 . D’après l’équation précédente, la température de sortie du compresseur, T 2s , est:
D’après la loi des gaz parfaits, nous savons que la chaleur spécifique molaire d’un gaz parfait monoatomique est:
C v = 3 / 2R = 12,5 J / mol K et C p = C v + R = 5 / 2R = 20,8 J / mol K
Nous transférons les capacités calorifiques spécifiques en unités de J / kg K via:
c p = C p . 1 / M (poids molaire de l’hélium) = 20,8 x 4,10 -3 = 5200 J / kg K
En utilisant cette température et l’ efficacité du compresseur isentropique, nous pouvons calculer la chaleur ajoutée par l’échangeur de chaleur:
Q add = c p (T 3 -T 1 ) – (c p (T 2s -T 1 ) / η K ) = 5200. (1190 – 299) – 5200. (424-299) /0,87 = 4,633 MJ / kg – 0,747 MJ / kg = 3,886 MJ / kg
……………………………………………………………………………………………………………………………….
Cet article est basé sur la traduction automatique de l’article original en anglais. Pour plus d’informations, voir l’article en anglais. Pouvez vous nous aider Si vous souhaitez corriger la traduction, envoyez-la à l’adresse: translations@nuclear-power.com ou remplissez le formulaire de traduction en ligne. Nous apprécions votre aide, nous mettrons à jour la traduction le plus rapidement possible. Merci