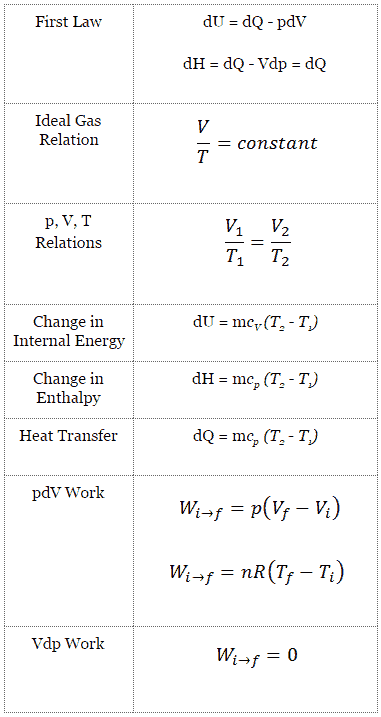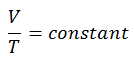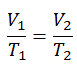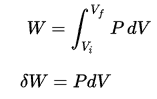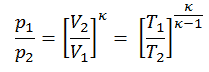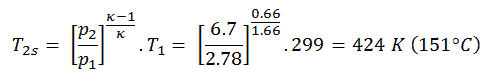Isobarer Prozess
Ein isobarer Prozess ist ein thermodynamischer Prozess , bei dem der Druck des Systems konstant bleibt (p = const). Die Wärmeübertragung in oder aus dem System funktioniert zwar, verändert aber auch die innere Energie des Systems.
Da sich die innere Energie (dU) und das Systemvolumen (∆V) ändern, verwenden Ingenieure häufig die Enthalpie des Systems, die wie folgt definiert ist:
H = U + pV
In vielen thermodynamischen Analysen ist es zweckmäßig, die Enthalpie anstelle der inneren Energie zu verwenden. Besonders im Fall des ersten Hauptsatzes der Thermodynamik .
Die Enthalpie ist der bevorzugte Ausdruck der Systemenergie, die sich bei vielen chemischen, biologischen und physikalischen Messungen bei konstantem Druck ändert . Es ist so nützlich, dass es in den Dampftabellen zusammen mit dem spezifischen Volumen und der spezifischen inneren Energie aufgeführt ist . Dies vereinfacht die Beschreibung der Energieübertragung . Bei konstantem Druck entspricht die Enthalpieänderung der Energie, die durch Erhitzen (Q = H 2 – H 1 ) oder andere Arbeiten als Expansionsarbeiten aus der Umgebung übertragen wird . Bei einem Prozess mit variablem Druck ist der Unterschied in der Enthalpie nicht ganz so offensichtlich.
Es gibt Ausdrücke in Bezug auf bekanntere Variablen wie Temperatur und Druck :
dH = C p dT + V (1-αT) dp
Dabei ist C p die Wärmekapazität bei konstantem Druck und α der Koeffizient der (kubischen) Wärmeausdehnung. Für ideales Gas ist αT = 1 und daher:
dH = C p dT
Für ein ideales Gas und einen polytropischen Prozess entspricht der Fall n = 0 einem isobaren Prozess (konstanter Druck). Im Gegensatz zum adiabatischen Prozess, bei dem n = und ein System keine Wärme mit seiner Umgebung austauscht (Q = 0; ∆T ≠ 0 ) , ändert sich bei einem isobaren Prozess die innere Energie (aufgrund von ∆T ≠ 0). und daher ΔU ≠ 0 (für ideale Gase) und Q ≠ 0.
In der Technik basieren beide sehr wichtigen thermodynamischen Kreisprozessen ( Brayton- und Rankine-Zyklus ) auf zwei isobaren Prozessen, daher ist die Untersuchung dieses Prozesses für Kraftwerke von entscheidender Bedeutung.
Isobarer Prozess und das erste Gesetz
Die klassische Form des ersten Hauptsatzes der Thermodynamik ist die folgende Gleichung:
dU = dQ – dW
In dieser Gleichung ist dW gleich dW = pdV und ist bekannt als die Grenz Arbeit .
Bei einem isobaren Prozess und dem idealen Gas wird ein Teil der dem System zugeführten Wärme für die Arbeit verwendet, und ein Teil der zugeführten Wärme erhöht die innere Energie (erhöht die Temperatur). Daher ist es zweckmäßig, die Enthalpie anstelle der inneren Energie zu verwenden. Da H = U + pV ist , ist dH = dU + pdV + Vdp und wir setzen dU = dH – pdV – Vdp in die klassische Form des Gesetzes ein:
dH – pdV – Vdp = dQ – pdV
Wir erhalten das Gesetz in Bezug auf die Enthalpie :
dH = dQ + Vdp
oder
dH = TdS + Vdp
In dieser Gleichung ist der Begriff Vdp eine Flussprozessarbeit. Diese Arbeit, Vdp , wird für Open-Flow-Systeme wie eine Turbine oder eine Pumpe verwendet, bei denen ein „dp“ vorliegt , dh eine Druckänderung. Es gibt keine Änderungen in der Lautstärke . Wie zu sehen ist, vereinfacht diese Form des Gesetzes die Beschreibung der Energieübertragung . Bei konstantem Druck entspricht die Enthalpieänderung der Energie , die durch Erhitzen aus der Umgebung übertragen wird:
Isobarer Prozess (Vdp = 0):
dH = dQ → Q = H 2 – H 1
Bei konstanter Entropie , dh im isentropischen Prozess, entspricht die Enthalpieänderung der am oder vom System durchgeführten Flussprozessarbeit .
Isentropischer Prozess (dQ = 0):
dH = Vdp → W = H 2 – H 1
Es ist offensichtlich, dass es bei der Analyse sowohl der in der Energietechnik verwendeten thermodynamischen Kreisprozessen, dh des Brayton-Zyklus als auch des Rankine-Zyklus, sehr nützlich sein wird.
Isobarer Prozess – Ideale Gasgleichung
Siehe auch: Was ist ein ideales Gas?
Nehmen wir eine isobare Wärmezufuhr in einem idealen Gas an. In einem idealen Gas haben Moleküle kein Volumen und interagieren nicht. Nach dem idealen Gasgesetz ändert sich der Druck linear mit Temperatur und Menge und umgekehrt mit dem Volumen .
pV = nRT
wo:
- p ist der absolute Druck des Gases
- n ist die Substanzmenge
- T ist die absolute Temperatur
- V ist die Lautstärke
- R ist die ideale oder universelle Gaskonstante, die dem Produkt der Boltzmann-Konstante und der Avogadro-Konstante entspricht.
In dieser Gleichung ist das Symbol R eine Konstante, die als universelle Gaskonstante bezeichnet wird und für alle Gase den gleichen Wert hat, nämlich R = 8,31 J / mol K.
Der isobare Prozess kann mit dem idealen Gasgesetz ausgedrückt werden als:
oder
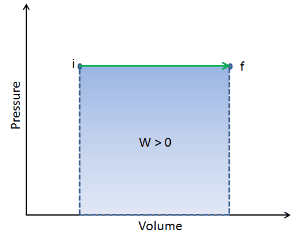
In einem pV-Diagramm erfolgt der Prozess entlang einer horizontalen Linie (Isobare genannt) mit der Gleichung p = Konstante.
Druck-Volumen-Arbeit durch das geschlossene System ist definiert als:
Unter der Annahme, dass die Menge des idealen Gases konstant bleibt und das ideale Gasgesetz angewendet wird , wird dies
Nach dem idealen Gasmodell kann die innere Energie berechnet werden durch:
∆U = mc v ∆T
wobei die Eigenschaft c v (J / mol K) als spezifische Wärme (oder Wärmekapazität ) bei konstantem Volumen bezeichnet wird, weil sie unter bestimmten besonderen Bedingungen (konstantes Volumen) die Temperaturänderung eines Systems mit der durch zugesetzten Energiemenge in Beziehung setzt Wärmeübertragung.
Addiert man diese Gleichungen, so erhält man die Gleichung für Wärme:
Q = mc v ∆T + m R ∆T = m (c v + R) ∆T = m c p ∆T
wobei die Eigenschaft c p (J / mol K) als spezifische Wärme (oder Wärmekapazität ) bei konstantem Druck bezeichnet wird.
Siehe auch: Spezifische Wärme bei konstantem Volumen und konstantem Druck
Siehe auch: Mayer-Formel
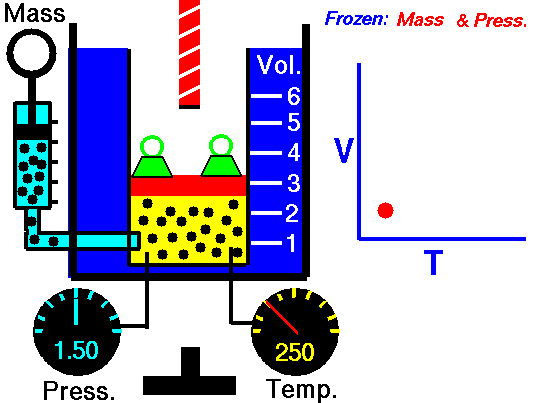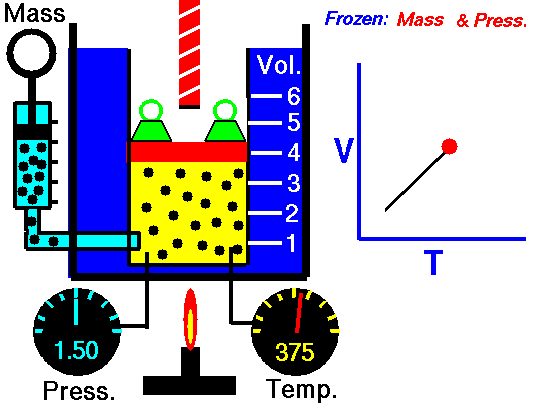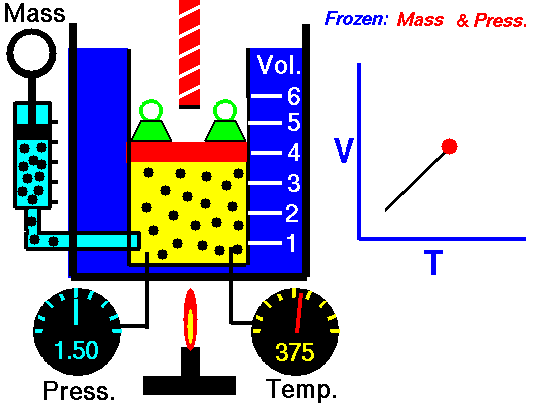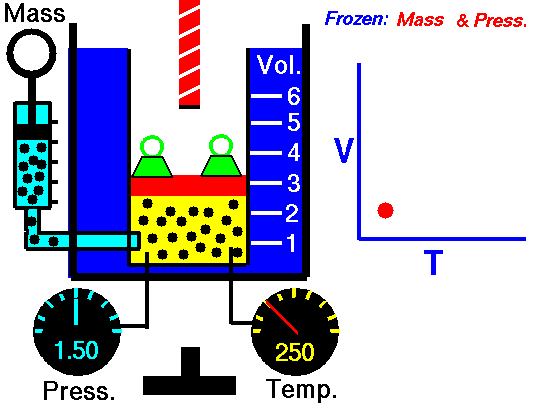
Charles ‘Gesetz
Charles ‘Gesetz ist eines der Gasgesetze. Ende des 18. Jahrhunderts untersuchte ein französischer Erfinder und Wissenschaftler, Jacques Alexandre César Charles, die Beziehung zwischen dem Volumen und der Temperatur eines Gases bei konstantem Druck . Die Ergebnisse bestimmter Experimente mit Gasen bei relativ niedrigem Druck veranlassten Jacques Alexandre César Charles, ein bekanntes Gesetz zu formulieren. Es sagt, dass:
Bei einer festen Gasmasse bei konstantem Druck ist das Volumen direkt proportional zur Kelvin-Temperatur.
Das heißt, wenn Sie beispielsweise die Temperatur verdoppeln, verdoppeln Sie die Lautstärke. Wenn Sie die Temperatur halbieren, halbieren Sie die Lautstärke.
Sie können dies mathematisch ausdrücken als:
V = konstant. T.
Ja, es scheint identisch zu sein mit dem isobaren Prozess des idealen Gases. Diese Ergebnisse stimmen voll und ganz mit dem idealen Gasgesetz überein , das bestimmt, dass die Konstante gleich nR / p ist . Wenn Sie die pV = nRT-Gleichung neu ordnen, indem Sie beide Seiten durch p teilen, erhalten Sie:
V = nR / p. T.
wobei nR / p konstant ist und:
- p ist der absolute Druck des Gases
- n ist die Substanzmenge
- T ist die absolute Temperatur
- V ist die Lautstärke
- R ist die ideale oder universelle Gaskonstante, die dem Produkt der Boltzmann-Konstante und der Avogadro-Konstante entspricht.
In dieser Gleichung ist das Symbol R eine Konstante, die als universelle Gaskonstante bezeichnet wird und für alle Gase den gleichen Wert hat, nämlich R = 8,31 J / mol K.
Beispiel eines isobaren Prozesses – Isobare Wärmezugabe

Nehmen wir den idealen Brayton-Zyklus an , der die Funktionsweise einer Wärmekraftmaschine mit konstantem Druck beschreibt . Moderne Gasturbinentriebwerke und luftatmende Strahltriebwerke folgen ebenfalls dem Brayton-Zyklus.
Der ideale Brayton-Zyklus besteht aus vier thermodynamischen Prozessen. Zwei isentrope Prozesse und zwei isobare Prozesse.
- isentropische Kompression – Umgebungsluft wird in den Kompressor gesaugt und dort unter Druck gesetzt (1 → 2). Die für den Kompressor erforderliche Arbeit ist gegeben durch W C = H 2 – H 1 .
- isobare Wärmezufuhr – Die Druckluft strömt dann durch eine Brennkammer, in der Kraftstoff verbrannt und Luft oder ein anderes Medium erwärmt wird (2 → 3). Es ist ein Prozess mit konstantem Druck, da die Kammer zum Ein- und Ausströmen geöffnet ist. Die hinzugefügte Nettowärme ist gegeben durch Q add = H 3 – H 2
- isentropische Expansion – Die erwärmte Druckluft dehnt sich dann auf der Turbine aus und gibt ihre Energie ab. Die von der Turbine geleistete Arbeit ist gegeben durch W T = H 4 – H 3
- isobare Wärmeabgabe – Die Restwärme muss abgeführt werden, um den Kreislauf zu schließen. Die abgegebene Nettowärme ist gegeben durch Q re = H 4 – H 1
Nehmen Sie eine isobare Wärmezufuhr (2 → 3) in einem Wärmetauscher an. In typischen Gasturbinen erhält die Hochdruckstufe Gas (Punkt 3 in der Abbildung; p 3 = 6,7 MPa ; T 3 = 1190 K (917 ° C)) von einem Wärmetauscher. Darüber hinaus wissen wir, dass der Kompressor Gas erhält (Punkt 1 in der Abbildung; p 1 = 2,78 MPa ; T 1 = 299 K (26 ° C)) und wir wissen, dass der isentrope Wirkungsgrad des Kompressors η K = 0,87 (87) beträgt %) .
Berechnen Sie die vom Wärmetauscher zugeführte Wärme (zwischen 2 → 3).
Lösung:
Nach dem ersten Hauptsatz der Thermodynamik ist die hinzugefügte Nettowärme gegeben durch Q add = H 3 – H 2 oder Q add = C p (T 3 -T 2s ), aber in diesem Fall kennen wir die Temperatur (T 2s nicht) ) am Auslass des Kompressors. Wir werden dieses Problem in intensiven Variablen lösen. Wir müssen die vorherige Gleichung (um η K einzuschließen ) unter Verwendung des Terms (+ h 1 – h 1 ) umschreiben, um:
Q add = h 3 – h 2 = h 3 – h 1 – (h 2s – h 1 ) / η K.
Q addiere = c p (T 3 -T 1 ) – (c p (T 2s -T 1 ) / η K )
Dann berechnen wir die Temperatur T 2s unter Verwendung der p, V, T-Beziehung für den adiabatischen Prozess zwischen (1 → 2).
In dieser Gleichung ist der Faktor für Helium gleich = c p / c v = 1,66 . Aus der vorherigen Gleichung folgt, dass die Kompressorauslasstemperatur T 2s ist:
Aus dem Idealgasgesetz wissen wir, dass die molare spezifische Wärme eines einatomigen Idealgases ist:
C v = 3 / 2R = 12,5 J / mol K und C p = C v + R = 5 / 2R = 20,8 J / mol K.
Wir übertragen die spezifischen Wärmekapazitäten in Einheiten von J / kg K über:
c p = C p . 1 / M (Molgewicht von Helium) = 20,8 · 4,10 & supmin; ³ = 5200 J / kg K.
Mit dieser Temperatur und dem Wirkungsgrad des isentropischen Kompressors können wir die vom Wärmetauscher zugeführte Wärme berechnen:
Q add = c p (T 3 -T 1 ) – (c p (T 2s -T 1 ) / η K ) = 5200. (1190 – 299) – 5200. (424-299) / 0,87 = 4,633 MJ / kg – 0,747 MJ / kg = 3,886 MJ / kg
……………………………………………………………………………………………………………………………….
Dieser Artikel basiert auf der maschinellen Übersetzung des englischen Originalartikels. Weitere Informationen finden Sie im Artikel auf Englisch. Sie können uns helfen. Wenn Sie die Übersetzung korrigieren möchten, senden Sie diese bitte an: translations@nuclear-power.com oder füllen Sie das Online-Übersetzungsformular aus. Wir bedanken uns für Ihre Hilfe und werden die Übersetzung so schnell wie möglich aktualisieren. Danke.