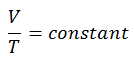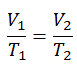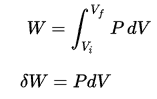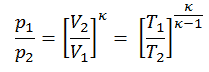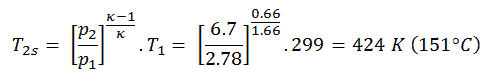Processo isobárico
Um processo isobárico é um processo termodinâmico , no qual a pressão do sistema permanece constante (p = const). A transferência de calor para dentro ou para fora do sistema funciona, mas também altera a energia interna do sistema.
Como existem mudanças na energia interna (dU) e no volume do sistema (∆V), os engenheiros costumam usar a entalpia do sistema, que é definida como:
H = U + pV
Em muitas análises termodinâmicas, é conveniente usar a entalpia em vez da energia interna. Especialmente no caso da primeira lei da termodinâmica .
A entalpia é a expressão preferida da energia do sistema que muda em muitas medições químicas, biológicas e físicas a pressão constante . É tão útil que é tabulado nas tabelas de vapor, juntamente com o volume específico e a energia interna específica . Isso se deve ao fato de simplificar a descrição da transferência de energia . Em pressão constante, a mudança de entalpia é igual à energia transferida do ambiente através do aquecimento (Q = H 2 – H 1 ) ou outro trabalho que não o trabalho de expansão. Para um processo de pressão variável, a diferença na entalpia não é tão óbvia.
Existem expressões em termos de variáveis mais familiares, como temperatura e pressão :
dH = C p dT + V (1-aT) dp
Onde C p é a capacidade calorífica a pressão constante e α é o coeficiente de expansão térmica (cúbico). Para o gás ideal αT = 1 e, portanto:
dH = C p dT
Para um gás ideal e um processo politrópico, o caso n = 0 corresponde a um processo isobárico (pressão constante). Ao contrário do processo adiabático, no qual n = e um sistema não troca calor com o ambiente (Q = 0; ∆T ≠ 0 ) , em um processo isobárico ocorre uma alteração na energia interna (devido a ∆T ≠ 0) e portanto ΔU ≠ 0 (para gases ideais) e Q ≠ 0.
Na engenharia, ambos os ciclos termodinâmicos muito importantes (ciclo de Brayton e Rankine ) são baseados em dois processos isobáricos, portanto, o estudo desse processo é crucial para as usinas de energia.
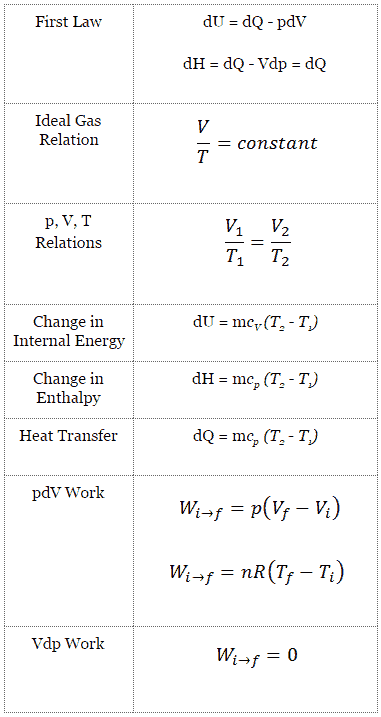
Processo isobárico e a primeira lei
A forma clássica da primeira lei da termodinâmica é a seguinte equação:
dU = dQ – dW
Nesta equação, dW é igual a dW = pdV e é conhecido como trabalho de fronteira .
Em um processo isobárico e no gás ideal, parte do calor adicionado ao sistema será usada para realizar o trabalho e parte do calor adicionado aumentará a energia interna (aumentará a temperatura). Portanto, é conveniente usar a entalpia em vez da energia interna. Desde H = U + pV , portanto dH = dU + pdV + Vdp e substituímos dU = dH – pdV – Vdp na forma clássica da lei:
dH – pdV – Vdp = dQ – pdV
Obtemos a lei em termos de entalpia :
dH = dQ + Vdp
ou
dH = TdS + Vdp
Nesta equação, o termo Vdp é um trabalho de processo de fluxo. Este trabalho, Vdp , é usado para sistemas de fluxo aberto como uma turbina ou uma bomba na qual existe um “dp” , ou seja, mudança de pressão. Não há alterações no volume de controle . Como pode ser visto, essa forma de lei simplifica a descrição da transferência de energia . A pressão constante , a mudança de entalpia é igual à energia transferida do ambiente através do aquecimento:
Processo isobárico (Vdp = 0):
dH = dQ → Q = H 2 – H 1
Na entropia constante , ou seja, no processo isentrópico, a mudança de entalpia é igual ao trabalho do processo de fluxo realizado no sistema ou pelo mesmo.
Processo isentrópico (dQ = 0):
dH = Vdp → W = H 2 – H 1
É óbvio que será muito útil na análise de ambos os ciclos termodinâmicos usados na engenharia de energia, ou seja, no ciclo de Brayton e no ciclo de Rankine.
Processo Isobárico – Equação Ideal de Gás
Veja também: O que é um gás ideal
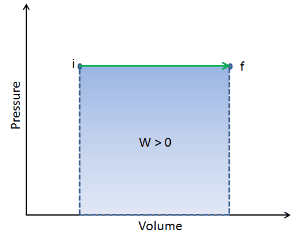
Vamos assumir uma adição isobárica de calor em um gás ideal. Num gás ideal , as moléculas não têm volume e não interagem. De acordo com a lei ideal dos gases , a pressão varia linearmente com a temperatura e a quantidade e inversamente com o volume .
pV = nRT
Onde:
- p é a pressão absoluta do gás
- n é a quantidade de substância
- T é a temperatura absoluta
- V é o volume
- R é a constante de gás ideal, ou universal, igual ao produto da constante de Boltzmann e da constante de Avogadro,
Nesta equação, o símbolo R é uma constante chamada constante universal de gás que tem o mesmo valor para todos os gases – ou seja, R = 8,31 J / mol K.
O processo isobárico pode ser expresso com a lei do gás ideal como:
ou
Em um diagrama de pV , o processo ocorre ao longo de uma linha horizontal (chamada isobar) que possui a equação p = constante.
O trabalho de volume de pressão pelo sistema fechado é definido como:
Assumindo que a quantidade de gás ideal permaneça constante e aplicando a lei do gás ideal , isso se torna
De acordo com o modelo de gás ideal, a energia interna pode ser calculada por:
∆U = mc v ∆T
onde a propriedade c v (J / mol K) é referida como calor específico (ou capacidade de calor ) a um volume constante porque, sob certas condições especiais (volume constante), relaciona a mudança de temperatura de um sistema à quantidade de energia adicionada por transferência de calor.
Somando essas equações, obtemos a equação para o calor:
Q = mc v ∆T + mR ∆T = m (c v + R) ∆T = m c p ∆T
onde a propriedade c p (J / mol K) é referido como calor específico (ou capacidade de calor ) a uma pressão constante.
Veja também: Calor específico a volume constante e pressão constante
Veja também: Fórmula de Mayer
Lei de Charles
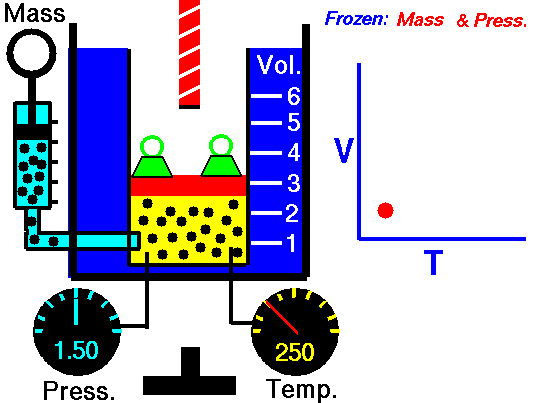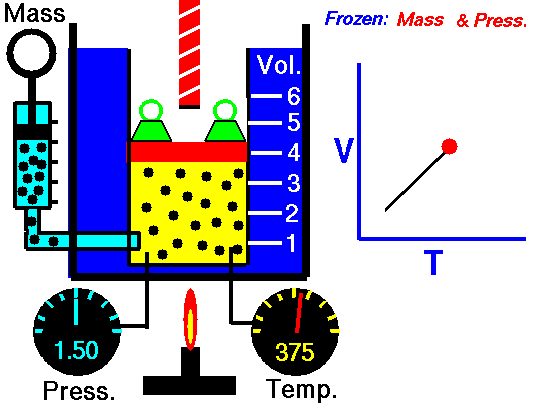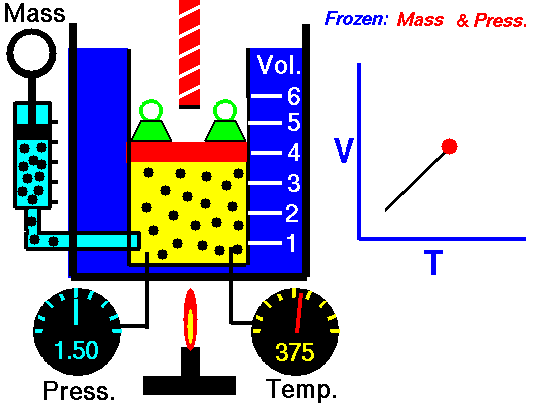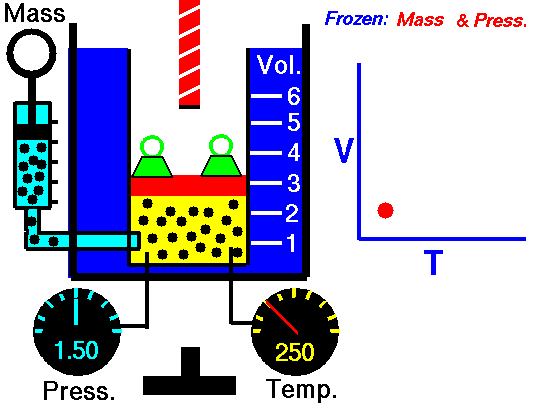
A lei de Charles é uma das leis de gás. No final do século XVIII, o inventor e cientista francês Jacques Alexandre César Charles estudou a relação entre o volume e a temperatura de um gás sob pressão constante . Os resultados de certas experiências com gases sob pressão relativamente baixa levaram Jacques Alexandre César Charles a formular uma lei bem conhecida. Afirma que:
Para uma massa fixa de gás a pressão constante, o volume é diretamente proporcional à temperatura Kelvin.
Isso significa que, por exemplo, se você dobrar a temperatura, dobrará o volume. Se você reduzir pela metade a temperatura, reduzirá pela metade o volume.
Você pode expressar isso matematicamente como:
V = constante. T
Sim, parece ser idêntico ao processo isobárico do gás ideal. Esses resultados são totalmente consistentes com a lei ideal dos gases , que determina que a constante é igual a nR / p . Se você reorganizar a equação pV = nRT dividindo os dois lados por p, obterá:
V = nR / p. T
onde nR / p é constante e:
- p é a pressão absoluta do gás
- n é a quantidade de substância
- T é a temperatura absoluta
- V é o volume
- R é a constante de gás ideal, ou universal, igual ao produto da constante de Boltzmann e da constante de Avogadro,
Nesta equação, o símbolo R é uma constante chamada constante universal de gás que tem o mesmo valor para todos os gases – ou seja, R = 8,31 J / mol K.
Exemplo de processo isobárico – adição de calor isobárico

Vamos assumir o ciclo de Brayton ideal que descreve o funcionamento de um motor de calor com pressão constante . Os modernos motores de turbina a gás e os motores a jato de respiração também seguem o ciclo de Brayton.
O ciclo ideal de Brayton consiste em quatro processos termodinâmicos. Dois processos isentrópicos e dois processos isobáricos.
- compressão isentrópica – o ar ambiente é aspirado para o compressor, onde é pressurizado (1 → 2). O trabalho necessário para o compressor é dado por W C = H 2 – H 1 .
- adição de calor isobárico – o ar comprimido passa por uma câmara de combustão, onde o combustível é queimado e o ar ou outro meio é aquecido (2 → 3). É um processo de pressão constante, já que a câmara está aberta para entrar e sair. O calor líquido adicionado é dado por Q add = H 3 – H 2
- expansão isentrópica – o ar aquecido e pressurizado se expande na turbina, gasta sua energia. O trabalho realizado pela turbina é dado por W T = H 4 – H 3
- rejeição de calor isobárica – o calor residual deve ser rejeitado para fechar o ciclo. O calor líquido rejeitado é dado por Q re = H 4 – H 1
Assuma uma adição de calor isobárica (2 → 3) em um trocador de calor. Em turbinas a gás típicas, o estágio de alta pressão recebe gás (ponto 3 na figura; p 3 = 6,7 MPa ; T 3 = 1190 K (917 ° C)) de um trocador de calor. Além disso, sabemos que o compressor recebe gás (ponto 1 na figura; p 1 = 2,78 MPa ; T 1 = 299 K (26 ° C)) e sabemos que a eficiência isentrópica do compressor é η K = 0,87 (87 %) .
Calcule o calor adicionado pelo trocador de calor (entre 2 → 3).
Solução:
A partir da primeira lei da termodinâmica , o calor acrescentado líquido é dada por Q add = H 3 – H 2 ou Q add = C p . (T 3 -T 2s ), mas neste caso não sabemos a temperatura (T 2s ) na saída do compressor. Vamos resolver esse problema em variáveis intensivas. Temos que reescrever a equação anterior (para incluir η K ) usando o termo (+ h 1 – h 1 ) para:
Q add = h 3 – h 2 = h 3 – h 1 – (h 2 s – h 1 ) / η K
Q add = c p (T 3 -T 1 ) – (c p (t 2s -T 1 ) / η K )
Em seguida, iremos calcular a temperatura, T 2s , usando P, V, T Relação de processo adiabático entre (1 → 2).
Nesta equação, o fator para o hélio é igual a = c p / c v = 1,66 . A partir da equação anterior segue-se que a temperatura de saída do compressor, t 2s , é:
De Lei do Gás Ideal sabemos, que o calor específico molar de um gás ideal monoatômico é:
C v = 3 / 2R = 12,5 J / mol K e C p = C v + R = 5 / 2R = 20,8 J / mol K
Transferimos as capacidades de calor específicas em unidades de J / kg K via:
c p = C p . 1 / M (peso molar de hélio) = 20,8 x 4,10 -3 = 5200 J / kg K
Usando esta temperatura e a eficiência isentrópica do compressor , podemos calcular o calor adicionado pelo trocador de calor:
Q add = c p (T 3 -T 1 ) – (c p (t 2s -T 1 ) / η K ) = 5200. (1190 – 299) – 5200. (424-299) /0.87 = 4,633 MJ / kg – 0,747 MJ / kg = 3,886 MJ / kg
……………………………………………………………………………………………………………………………….
Este artigo é baseado na tradução automática do artigo original em inglês. Para mais informações, consulte o artigo em inglês. Você pode nos ajudar. Se você deseja corrigir a tradução, envie-a para: translations@nuclear-power.com ou preencha o formulário de tradução on-line. Agradecemos sua ajuda, atualizaremos a tradução o mais rápido possível. Obrigado.