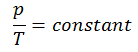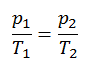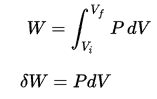Processus isochorique – Processus isométrique
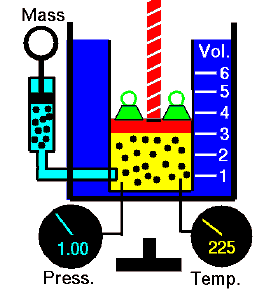
Un processus isochore est un processus thermodynamique, dans lequel le volume du système fermé reste constant (V = const). Il décrit le comportement du gaz à l’intérieur du conteneur, qui ne peut pas être déformé. Étant donné que le volume reste constant, le transfert de chaleur dans ou hors du système ne fonctionne pas avec le p∆V , mais modifie uniquement l’ énergie interne (la température) du système.
Pour un gaz parfait et un processus polytropique , le cas n ➝ ∞ correspond à un processus isochore (volume constant) . Contrairement au processus adiabatique , dans lequel n = et un système n’échange pas de chaleur avec son environnement (Q = 0; W ≠ 0 ) , dans un processus isochore, il y a un changement dans l’énergie interne (due à ∆T ≠ 0) et donc ΔU ≠ 0 (pour les gaz parfaits) et (Q ≠ 0; W = 0 ).
Dans l’ingénierie des moteurs à combustion interne , les processus isochoriques sont très importants pour leurs cycles thermodynamiques (cycle Otto et Diesel), donc l’étude de ce processus est cruciale pour l’ingénierie automobile.
Processus isochorique et première loi
La forme classique de la première loi de la thermodynamique est l’équation suivante:
dU = dQ – dW
Dans cette équation, dW est égal à dW = pdV et est connu comme le travail aux limites . Alors:
dU = dQ – pdV
Dans le processus isochore et le gaz parfait, toute la chaleur ajoutée au système sera utilisée pour augmenter l’énergie interne.
Processus isochorique (pdV = 0):
dU = dQ (pour le gaz parfait)
Processus isochorique – Équation du gaz parfait
Voir aussi: Qu’est-ce qu’un gaz parfait
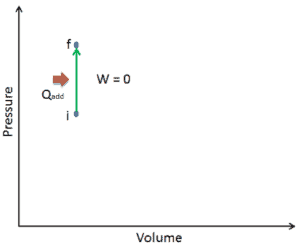Supposons un apport de chaleur isochore dans un gaz parfait. Dans un gaz parfait , les molécules n’ont pas de volume et n’interagissent pas. Selon la loi du gaz parfait , la pression varie linéairement avec la température et la quantité, et inversement avec le volume .
pV = nRT
où:
- p est la pression absolue du gaz
- n est la quantité de substance
- T est la température absolue
- V est le volume
- R est la constante de gaz parfaite ou universelle, égale au produit de la constante de Boltzmann et de la constante d’Avogadro,
Dans cette équation, le symbole R est une constante appelée constante de gaz universelle qui a la même valeur pour tous les gaz, à savoir R = 8,31 J / mol K.
Le processus isochore peut s’exprimer avec la loi du gaz parfait comme:
ou
Sur un diagramme pV , le processus se produit le long d’une ligne horizontale qui a l’équation V = constante.
Le travail pression-volume par le système fermé est défini comme:
Le processus étant isochore , dV = 0 , le travail pression-volume est égal à zéro . Selon le modèle de gaz parfait, l’énergie interne peut être calculée par:
∆U = mc v ∆T
lorsque la propriété c v (J / mol K) est appelée chaleur spécifique (ou capacité calorifique ) à volume constant car, dans certaines conditions spéciales (volume constant), elle relie le changement de température d’un système à la quantité d’énergie ajoutée par transfert de chaleur.
Puisqu’il n’y a aucun travail effectué par ou sur le système, la première loi de la thermodynamique dicte ∆U = ∆Q. Donc:
Q = mc v ∆T
Voir aussi: Chaleur spécifique à volume constant et pression constante
Voir aussi: formule de Mayer
Loi de Guy-Lussac
La loi de Guy-Lussac ou la loi sur la pression, l’ une des lois sur le gaz, stipule que:
Pour une masse fixe de gaz à volume constant, la pression est directement proportionnelle à la température Kelvin.
Cela signifie que, par exemple, si vous doublez la température, vous doublerez la pression. Si vous divisez par deux la température, vous réduisez de moitié la pression.
Vous pouvez exprimer cela mathématiquement comme:
p = constant. T
Oui, il semble être identique au processus isochore du gaz parfait. Ces résultats sont parfaitement cohérents avec la loi du gaz parfait, qui détermine que la constante est égale à nR / V. Si vous réorganisez l’équation pV = nRT en divisant les deux côtés par V, vous obtiendrez:
p = nR / V. T
où nR / V est constant et:
- p est la pression absolue du gaz
- n est la quantité de substance
- T est la température absolue
- V est le volume
- R est la constante de gaz parfaite ou universelle, égale au produit de la constante de Boltzmann et de la constante d’Avogadro
Exemple de processus isochorique – Addition de chaleur isochorique
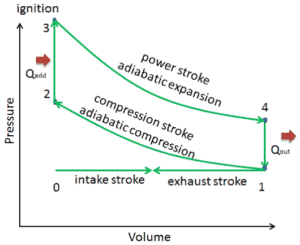Supposons le cycle Otto , qui est l’un des cycles thermodynamiques les plus courants que l’on puisse trouver dans les moteurs d’automobiles . Ce cycle suppose que l’apport de chaleur se produit instantanément ( entre 2 → 3 ) alors que le piston est au point mort haut. Ce processus est considéré comme isochore.
Les processus 2 → 3 et 4 → 1 sont des processus isochoriques , dans lesquels la chaleur est transférée dans le système entre 2 → 3 et hors du système entre 4 → 1. Pendant ces processus, aucun travail n’est effectué sur le système ou extrait du système . Le processus isochore 2 → 3 est censé représenter l’inflammation du mélange carburant-air et la combustion rapide qui en résulte.
Cet article est basé sur la traduction automatique de l’article original en anglais. Pour plus d’informations, voir l’article en anglais. Pouvez vous nous aider Si vous souhaitez corriger la traduction, envoyez-la à l’adresse: translations@nuclear-power.com ou remplissez le formulaire de traduction en ligne. Nous apprécions votre aide, nous mettrons à jour la traduction le plus rapidement possible. Merci
