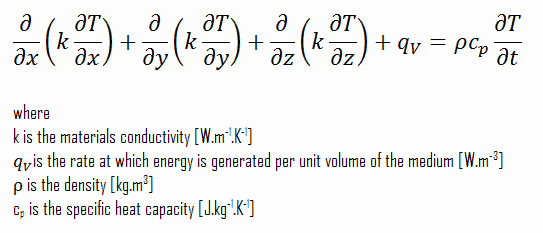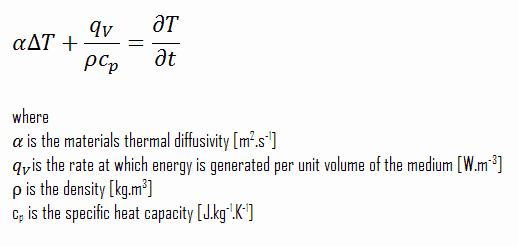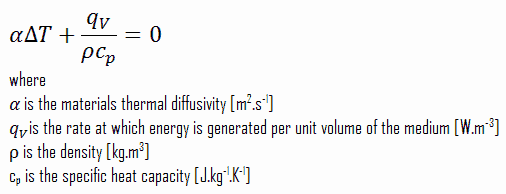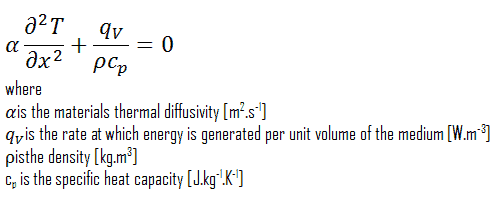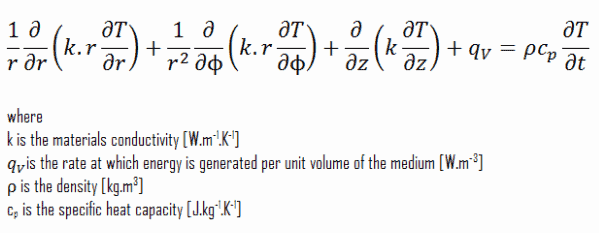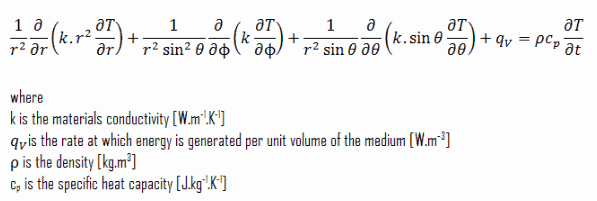Ecuación de calor – Ecuación de conducción de calor
En secciones anteriores, hemos tratado especialmente la transferencia de calor unidimensional en estado estacionario, que puede caracterizarse por la ley de conducción de calor de Fourier . Pero su aplicabilidad es muy limitada. Esta ley supone la transferencia de calor en estado estable a través de un cuerpo plano (tenga en cuenta que la ley de Fourier se puede derivar también para coordenadas cilíndricas y esféricas), sin fuentes de calor . Es simplemente la ecuación de velocidad en este modo de transferencia de calor, donde se conoce el gradiente de temperatura.
Pero un problema importante en la mayoría de los análisis de conducción es determinar el campo de temperatura en un medio resultante de las condiciones impuestas en sus límites. En ingeniería, tenemos que resolver problemas de transferencia de calor que involucran diferentes geometrías y diferentes condiciones, como un elemento cilíndrico de combustible nuclear, que involucra una fuente interna de calor o la pared de una contención esférica. Estos problemas son más complejos que los análisis planos que hicimos en secciones anteriores. Por lo tanto, estos problemas serán el tema de esta sección, en la cual se introducirá y resolverá la ecuación de conducción de calor .
Ecuación general de conducción de calor
La ecuación de conducción de calor es una ecuación diferencial parcial que describe la distribución de calor (o el campo de temperatura ) en un cuerpo dado a lo largo del tiempo. El conocimiento detallado del campo de temperatura es muy importante en la conducción térmica a través de materiales. Una vez que se conoce esta distribución de temperatura, el flujo de calor de conducción en cualquier punto del material o en su superficie puede calcularse a partir de la ley de Fourier .
La ecuación del calor se deriva de la ley de Fourier y la conservación de la energía . La ley de Fourier establece que la tasa de tiempo de transferencia de calor a través de un material es proporcional al gradiente negativo en la temperatura y al área, en ángulo recto a ese gradiente, a través del cual fluye el calor.
Un cambio en la energía interna por unidad de volumen en el material, ΔQ, es proporcional al cambio de temperatura, Δu. Es decir:
∆Q = ρ.c p .∆T
Forma general
Usando estas dos ecuaciones podemos derivar la ecuación general de conducción de calor:
Esta ecuación también se conoce como la ecuación de Fourier-Biot , y proporciona la herramienta básica para el análisis de conducción de calor. A partir de su solución, podemos obtener el campo de temperatura en función del tiempo.
En palabras, la ecuación de conducción de calor establece que:
En cualquier punto del medio, la tasa neta de transferencia de energía por conducción en un volumen unitario más la tasa volumétrica de generación de energía térmica debe ser igual a la tasa de cambio de energía térmica almacenada dentro del volumen.
Conductividad térmica constante
Esta ecuación se puede reducir aún más suponiendo que la conductividad térmica sea constante e introduciendo la difusividad térmica, α = k / ρc p :
Ecuación de calor unidimensional
Una de las suposiciones más poderosas es que el caso especial de transferencia de calor unidimensional en la dirección x. En este caso, las derivadas con respecto a y y z caen y las ecuaciones anteriores se reducen a (coordenadas cartesianas):
Conducción de calor en coordenadas cilíndricas y esféricas.
En ingeniería, hay muchos problemas que no se pueden resolver en coordenadas cartesianas. Los sistemas cilíndricos y esféricos son muy comunes en térmica y especialmente en ingeniería de energía. La ecuación de calor también se puede expresar en coordenadas cilíndricas y esféricas. La ecuación general de conducción de calor en coordenadas cilíndricas puede obtenerse a partir de un balance de energía en un elemento de volumen en coordenadas cilíndricas y utilizando el operador de Laplace, Δ, en forma cilíndrica y esférica .
Coordenadas cilíndricas:
Coordenadas esféricas
La obtención de soluciones analíticas para estas ecuaciones diferenciales requiere un conocimiento de las técnicas de solución de ecuaciones diferenciales parciales, que está más allá del alcance de este texto. Por otro lado, hay muchas simplificaciones y suposiciones que se pueden aplicar a estas ecuaciones y que conducen a resultados muy importantes. En la siguiente sección, limitamos nuestra consideración a casos de estado estacionario unidimensionales con conductividad térmica constante, ya que resultan en ecuaciones diferenciales ordinarias.
Límite y condiciones iniciales
En cuanto a otra ecuación diferencial , la solución está dada por los límites y las condiciones iniciales . Con respecto a las condiciones de contorno, existen varias posibilidades comunes que simplemente se expresan en forma matemática.
Debido a que la ecuación de calor es de segundo orden en las coordenadas espaciales, para describir un problema de transferencia de calor por completo, se deben dar dos condiciones límite para cada dirección del sistema de coordenadas a lo largo de la cual la transferencia de calor es significativa. Por lo tanto, necesitamos especificar cuatro condiciones límite para problemas bidimensionales y seis condiciones límite para problemas tridimensionales.
En la siguiente sección se resumen cuatro tipos de condiciones límite comúnmente encontradas en la transferencia de calor:
Conducción con generación de calor.
En la sección anterior consideramos problemas de conducción térmica sin fuentes internas de calor . Para estos problemas, la distribución de temperatura en un medio se determinó únicamente por las condiciones en los límites del medio. Pero en ingeniería a menudo podemos encontrar un problema, en el que las fuentes de calor internas son importantes y determinan la distribución de temperatura junto con las condiciones de contorno.
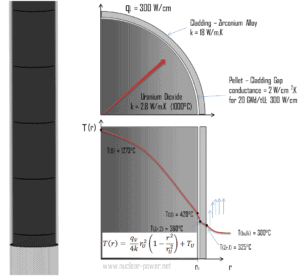
En ingeniería nuclear , estos problemas son de la mayor importancia, ya que la mayor parte del calor generado en el combustible nuclear se libera dentro de los gránulos de combustible y la distribución de temperatura está determinada principalmente por la distribución de generación de calor. Tenga en cuenta que, como se puede ver en la descripción de los componentes individuales de la energía energética total liberada durante la reacción de fisión, se genera una cantidad significativa de energía fuera del combustible nuclear (barras de combustible externas). Especialmente la energía cinética de los neutrones rápidos se genera en gran medida en el refrigerante ( moderador ) . Este fenómeno necesita ser incluido en los cálculos nucleares.
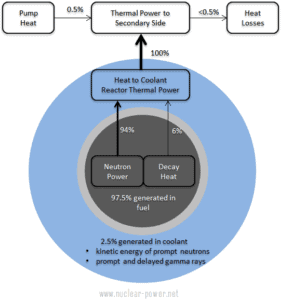
Para LWR , generalmente se acepta que aproximadamente el 2.5% de la energía total se recupera en el moderador . Esta fracción de energía depende de los materiales, su disposición dentro del reactor y, por lo tanto, del tipo de reactor.
Tenga en cuenta que la generación de calor es un fenómeno volumétrico. Es decir, ocurre en todo el cuerpo de un medio. Por lo tanto, la tasa de generación de calor en un medio generalmente se especifica por unidad de volumen y se denota por g V [W / m 3 ] .
La distribución de temperatura y, en consecuencia, el flujo de calor está determinada principalmente por:
- Geometría y condiciones de contorno . Geometría diferente conduce a un campo de temperatura completamente diferente.
- Tasa de generación de calor . La caída de temperatura a través del cuerpo aumentará con el aumento de la generación de calor.
- Conductividad térmica del medio . Una conductividad térmica más alta conducirá a una caída de temperatura más baja.
……………………………………………………………………………………………………………………………….
Este artículo se basa en la traducción automática del artículo original en inglés. Para más información vea el artículo en inglés. Puedes ayudarnos. Si desea corregir la traducción, envíela a: translations@nuclear-power.com o complete el formulario de traducción en línea. Agradecemos su ayuda, actualizaremos la traducción lo antes posible. Gracias.
