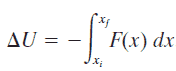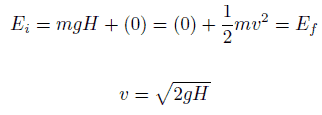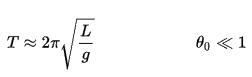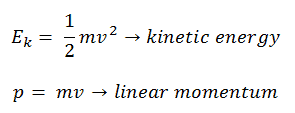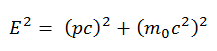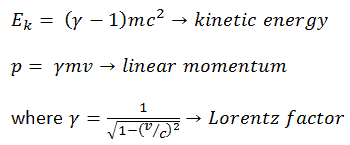¿Qué es la energía cinética?
La energía cinética, K , se define como la energía almacenada en un objeto debido a su movimiento. Un objeto en movimiento tiene la capacidad de hacer trabajo y, por lo tanto, se puede decir que tiene energía. Se llama energía cinética, de la palabra griega kinetikos, que significa “movimiento”.
La energía cinética depende de la velocidad de un objeto y es la capacidad de un objeto en movimiento para trabajar en otros objetos cuando choca con ellos. Por otro lado, la energía cinética de un objeto representa la cantidad de energía requerida para aumentar la velocidad del objeto desde el reposo (v = 0) hasta su velocidad final. La energía cinética también depende linealmente de la masa, que es una medida numérica de la inercia del objeto y la medida de la resistencia de un objeto a la aceleración cuando se aplica una fuerza.
Definimos la cantidad:
K = ½ mv 2
ser la energía cinética traslacional del objeto. Debe agregarse, se llama energía cinética “traslacional” para distinguirla de la energía cinética rotacional.
Conservación de la energía mecánica.
Primero se declaró el principio de Conservación de la Energía Mecánica :
La energía mecánica total (definida como la suma de su potencial y energías cinéticas) de una partícula sobre la que actúan solo fuerzas conservadoras es constante .
Ver también: Conservación de la energía mecánica.
Un sistema aislado es aquel en el que ninguna fuerza externa causa cambios de energía. Si solo las fuerzas conservadoras actúan sobre un objeto y U es la función de energía potencial para la fuerza conservadora total, entonces
E mech = U + K
La energía potencial, U , depende de la posición de un objeto sometido a una fuerza conservadora.
Se define como la capacidad del objeto para hacer trabajo y aumenta a medida que el objeto se mueve en la dirección opuesta a la dirección de la fuerza.
La energía potencial asociada con un sistema que consiste en la Tierra y una partícula cercana es la energía potencial gravitacional .
La energía cinética, K , depende de la velocidad de un objeto y es la capacidad de un objeto en movimiento para trabajar en otros objetos cuando choca con ellos.
K = ½ mv 2
La definición mencionada anteriormente ( E mech = U + K ) supone que el sistema está libre de fricción y otras fuerzas no conservativas . La diferencia entre una fuerza conservadora y una no conservadora es que cuando una fuerza conservadora mueve un objeto de un punto a otro, el trabajo realizado por la fuerza conservadora es independiente del camino.
En cualquier situación real, las fuerzas de fricción y otras fuerzas no conservativas están presentes, pero en muchos casos sus efectos en el sistema son tan pequeños que el principio de conservación de la energía mecánica puede usarse como una aproximación justa. Por ejemplo, la fuerza de fricción es una fuerza no conservativa, porque actúa para reducir la energía mecánica en un sistema.
Tenga en cuenta que las fuerzas no conservativas no siempre reducen la energía mecánica. Una fuerza no conservadora cambia la energía mecánica, hay fuerzas que aumentan la energía mecánica total, como la fuerza proporcionada por un motor o motor, también es una fuerza no conservativa.
Bloque deslizándose por una pendiente inclinada sin fricción
El bloque de 1 kg comienza a una altura H (digamos 1 m) sobre el suelo, con energía potencial mgH y energía cinética que es igual a 0. Se desliza hacia el suelo (sin fricción) y llega sin energía potencial y energía cinética. K = ½ mv 2 . Calcule la velocidad del bloque en el suelo y su energía cinética.
E mech = U + K = constante
=> ½ mv 2 = mgH
=> v = √2gH = 4.43 m / s
=> K 2 = ½ x 1 kg x (4.43 m / s) 2 = 19.62 kg.m 2 .s -2 = 19.62 J
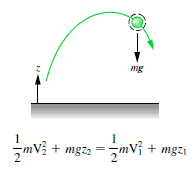
Péndulo
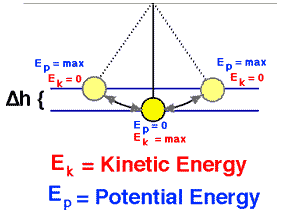Suponga un péndulo (bola de masa m suspendida en una cuerda de longitud L que hemos levantado para que la bola esté a una altura H <L por encima de su punto más bajo en el arco de su movimiento de cuerda estirada. El péndulo está sujeto al conservador fuerza gravitacional donde las fuerzas de fricción como el arrastre de aire y la fricción en el pivote son insignificantes.
Lo liberamos del reposo. ¿Qué tan rápido va en la parte inferior?
El péndulo alcanza la mayor energía cinética y la menor energía potencial cuando está en posición vertical , porque tendrá la mayor velocidad y estará más cerca de la Tierra en este punto. Por otro lado, tendrá la menor energía cinética y la mayor energía potencial en las posiciones extremas de su oscilación, porque tiene velocidad cero y está más lejos de la Tierra en estos puntos.
Si la amplitud se limita a pequeñas oscilaciones, el período T de un péndulo simple, el tiempo necesario para un ciclo completo, es:
donde L es la longitud del péndulo yg es la aceleración local de la gravedad. Para columpios pequeños, el período de columpio es aproximadamente el mismo para columpios de diferentes tamaños. Es decir, el período es independiente de la amplitud .
Energía cinética relativista
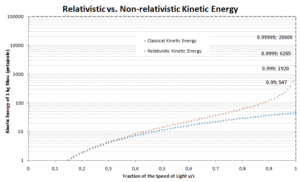
La relación previa entre el trabajo y la energía cinética se basa en las leyes del movimiento de Newton . Cuando generalizamos estas leyes de acuerdo con el principio de relatividad, necesitamos una generalización correspondiente de la ecuación para la energía cinética . Si la velocidad de un objeto está cerca de la velocidad de la luz, es necesario utilizar una mecánica relativista para calcular su energía cinética .
En mecánica clásica , la energía cinética y el momento se expresan como:
La derivación de sus relaciones relativistas se basa en la relación relativista energía-momento:
Se puede derivar, la energía cinética relativista y el momento relativista son:
El primer término ( ɣmc 2 ) de la energía cinética relativista aumenta con la velocidad v de la partícula. El segundo término ( mc 2 ) es constante; Se llama energía en reposo (masa en reposo) de la partícula, y representa una forma de energía que tiene una partícula incluso cuando está a velocidad cero . Cuando la velocidad de un objeto se acerca a la velocidad de la luz, la energía cinética se acerca al infinito . Es causada por el factor Lorentz , que se acerca al infinito para v → c . Por lo tanto, la velocidad de la luz no puede ser alcanzada por ninguna partícula masiva.
El primer término (ɣmc 2 ) se conoce como la energía total E de la partícula, porque es igual a la energía en reposo más la energía cinética:
E = K + mc 2
Para una partícula en reposo, es decir, K es cero, por lo que la energía total es su energía en reposo:
E = mc 2
Este es uno de los resultados sorprendentes de la teoría de la relatividad de Einstein es que la masa y la energía son equivalentes y convertibles una en la otra. La famosa fórmula E = mc 2 describe la equivalencia de la masa y la energía . Este resultado ha sido confirmado experimentalmente innumerables veces en física de partículas nucleares y elementales. Por ejemplo, vea Producción de pares de positrones-electrones o Conservación de energía en reacciones nucleares .
Ver también: masa relativista
Ejemplo: energía cinética de protón
Un protón ( m = 1.67 x 10 -27 kg ) viaja a una velocidad v = 0.9900c = 2.968 x 10 8 m / s . ¿Cuál es su energía cinética ?
Según un cálculo clásico, que no es correcto, obtendríamos:
K = 1 / 2mV 2 = ½ x (1,67 x 10 -27 kg) x (2.968 x 10 8 m / s) 2 = 7,355 x 10 -11 J
Con la corrección relativista, la energía cinética relativista es igual a:
K = (ɣ – 1) mc 2
donde el factor de Lorentz
ɣ = 7.089
por lo tanto
K = 6.089 x (1.67 x 10 -27 kg) x (2.9979 x 10 8 m / s) 2 = 9.139 x 10-10 J = 5.701 GeV
Esto es aproximadamente 12 veces más energía que en el cálculo clásico. De acuerdo con esta relación, una aceleración de un haz de protones a 5.7 GeV requiere energías que son diferentes en el orden.
……………………………………………………………………………………………………………………………….
Este artículo se basa en la traducción automática del artículo original en inglés. Para más información vea el artículo en inglés. Puedes ayudarnos. Si desea corregir la traducción, envíela a: translations@nuclear-power.com o complete el formulario de traducción en línea. Agradecemos su ayuda, actualizaremos la traducción lo antes posible. Gracias.
