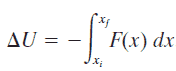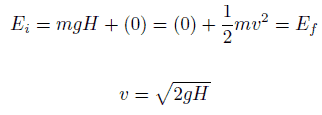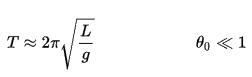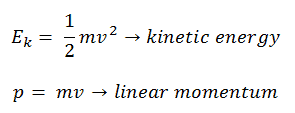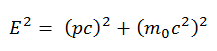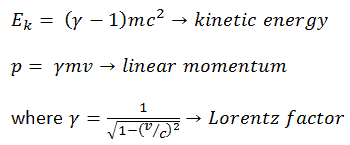Was ist kinetische Energie?
Die kinetische Energie K ist definiert als die Energie, die aufgrund ihrer Bewegung in einem Objekt gespeichert ist. Ein in Bewegung befindliches Objekt hat die Fähigkeit zu arbeiten und kann somit als energiereich bezeichnet werden. Es wird kinetische Energie genannt, vom griechischen Wort kinetikos, was “Bewegung” bedeutet.
Die kinetische Energie hängt von der Geschwindigkeit eines Objekts ab und ist die Fähigkeit eines sich bewegenden Objekts, an anderen Objekten zu arbeiten, wenn es mit ihnen kollidiert. Andererseits stellt die kinetische Energie eines Objekts die Energiemenge dar, die erforderlich ist, um die Geschwindigkeit des Objekts aus dem Ruhezustand (v = 0) auf seine Endgeschwindigkeit zu erhöhen. Die kinetische Energie hängt auch linear von der Masse ab, die ein numerisches Maß für die Trägheit des Objekts und das Maß für den Widerstand eines Objekts gegen die Beschleunigung ist, wenn eine Kraft ausgeübt wird.
Wir definieren die Menge:
K = 1/2 mv 2
die translatorische kinetische Energie des Objekts zu sein. Es muss hinzugefügt werden, es wird die “translatorische” kinetische Energie genannt, um es von der kinetischen Rotationsenergie zu unterscheiden.
Erhaltung der mechanischen Energie
Zunächst wurde das Prinzip der Erhaltung der mechanischen Energie festgelegt:
Die gesamte mechanische Energie (definiert als die Summe ihrer potentiellen und kinetischen Energien) eines Teilchens, auf das nur konservative Kräfte einwirken, ist konstant .
Siehe auch: Erhaltung der mechanischen Energie
Ein isoliertes System ist ein System, bei dem keine äußere Kraft Energieänderungen verursacht. Wenn nur konservative Kräfte auf ein Objekt wirken und U die potentielle Energiefunktion für die gesamte konservative Kraft ist, dann
E mech = U + K.
Die potentielle Energie U hängt von der Position eines Objekts ab, das einer konservativen Kraft ausgesetzt ist.
Es ist definiert als die Arbeitsfähigkeit des Objekts und wird erhöht, wenn das Objekt in die entgegengesetzte Richtung der Kraftrichtung bewegt wird.
Die potentielle Energie, die mit einem System verbunden ist, das aus der Erde und einem nahe gelegenen Teilchen besteht, ist potentielle Gravitationsenergie .
Die kinetische Energie K hängt von der Geschwindigkeit eines Objekts ab und ist die Fähigkeit eines sich bewegenden Objekts, an anderen Objekten zu arbeiten, wenn es mit ihnen kollidiert.
K = ½ mv 2
Die oben erwähnte Definition ( E mech = U + K ) setzt voraus, dass das System frei von Reibung und anderen nicht konservativen Kräften ist . Der Unterschied zwischen einer konservativen und einer nichtkonservativen Kraft besteht darin, dass die Arbeit der konservativen Kraft unabhängig vom Pfad ist, wenn eine konservative Kraft ein Objekt von einem Punkt zum anderen bewegt.
In jeder realen Situation sind Reibungskräfte und andere nicht konservative Kräfte vorhanden, aber in vielen Fällen sind ihre Auswirkungen auf das System so gering, dass das Prinzip der Erhaltung mechanischer Energie als angemessene Annäherung verwendet werden kann. Zum Beispiel ist die Reibungskraft eine nicht konservative Kraft, weil sie die mechanische Energie in einem System reduziert.
Beachten Sie, dass nicht konservative Kräfte die mechanische Energie nicht immer reduzieren. Eine nicht konservative Kraft verändert die mechanische Energie, es gibt Kräfte, die die gesamte mechanische Energie erhöhen, wie die von einem Motor oder Motor bereitgestellte Kraft, die ebenfalls eine nicht konservative Kraft ist.
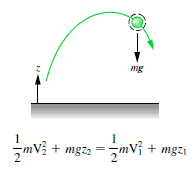
Block rutschen eine reibungslose Steigung hinunter
Der 1-kg-Block beginnt eine Höhe H (sagen wir 1 m) über dem Boden mit einer potentiellen Energie mgH und einer kinetischen Energie von 0. Er gleitet auf den Boden (ohne Reibung) und kommt ohne potentielle Energie und kinetische Energie an K = ½ mv 2 . Berechnen Sie die Geschwindigkeit des Blocks am Boden und seine kinetische Energie.
E mech = U + K = const
=> ½ mv 2 = mgH
=> v = √2gH = 4,43 m / s
=> K 2 = ½ x 1 kg x (4,43 m / s) 2 = 19,62 kg.m 2 .s -2 = 19,62 J
Pendel
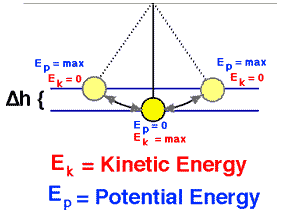Nehmen Sie ein Pendel an (Kugel der Masse m, die an einer Schnur der Länge L aufgehängt ist , die wir hochgezogen haben, so dass die Kugel eine Höhe H <L über ihrem tiefsten Punkt im Bogen ihrer Bewegung der gedehnten Schnur liegt. Das Pendel wird dem Konservativen unterworfen Gravitationskraft, bei der Reibungskräfte wie Luftwiderstand und Reibung am Drehpunkt vernachlässigbar sind.
Wir befreien es von der Ruhe. Wie schnell geht es unten?
Das Pendel erreicht in vertikaler Position die größte kinetische Energie und die geringste potentielle Energie , da es die größte Geschwindigkeit hat und an diesem Punkt der Erde am nächsten ist. Andererseits hat es an den extremen Positionen seines Schwungs seine geringste kinetische Energie und seine größte potentielle Energie , da es keine Geschwindigkeit hat und an diesen Punkten am weitesten von der Erde entfernt ist.
Wenn die Amplitude auf kleine Schwankungen begrenzt ist, beträgt die Periode T eines einfachen Pendels, die Zeit, die für einen vollständigen Zyklus benötigt wird:
Dabei ist L die Länge des Pendels und g die lokale Erdbeschleunigung. Bei kleinen Schaukeln ist die Schwungdauer für Schaukeln unterschiedlicher Größe ungefähr gleich. Das heißt, die Periode ist unabhängig von der Amplitude .
Relativistische kinetische Energie
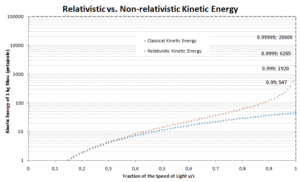
Die bisherige Beziehung zwischen Arbeit und kinetischer Energie basiert auf Newtons Bewegungsgesetzen . Wenn wir diese Gesetze nach dem Relativitätsprinzip verallgemeinern, brauchen wir eine entsprechende Verallgemeinerung der Gleichung für kinetische Energie . Wenn die Geschwindigkeit eines Objekts nahe an der Lichtgeschwindigkeit liegt, muss eine relativistische Mechanik verwendet werden , um seine kinetische Energie zu berechnen .
In der klassischen Mechanik werden kinetische Energie und Impuls ausgedrückt als:
Die Ableitung seiner relativistischen Beziehungen basiert auf der relativistischen Energie-Impuls-Beziehung:
Es kann abgeleitet werden, dass die relativistische kinetische Energie und der relativistische Impuls sind:
Der erste Term ( ɣmc 2 ) der relativistischen kinetischen Energie nimmt mit der Geschwindigkeit v des Teilchens zu. Der zweite Term ( mc 2 ) ist konstant; Es wird die Ruheenergie (Ruhemasse) des Partikels genannt und stellt eine Energieform dar, die ein Partikel selbst bei einer Geschwindigkeit von Null hat . Wenn sich die Geschwindigkeit eines Objekts der Lichtgeschwindigkeit nähert, nähert sich die kinetische Energie der Unendlichkeit . Es wird durch den Lorentz-Faktor verursacht , der für v → c gegen unendlich geht . Daher kann die Lichtgeschwindigkeit von keinen massiven Partikeln erreicht werden.
Der erste Term (ɣmc 2 ) ist als Gesamtenergie E des Teilchens bekannt, da er der Restenergie plus der kinetischen Energie entspricht:
E = K + mc 2
Für ein Teilchen in Ruhe ist K Null, also ist die Gesamtenergie seine Ruheenergie:
E = mc 2
Dies ist eines der bemerkenswerten Ergebnisse von Einsteins Relativitätstheorie : Masse und Energie sind äquivalent und ineinander umwandelbar . Die Äquivalenz von Masse und Energie wird durch Einsteins berühmte Formel E = mc 2 beschrieben . Dieses Ergebnis wurde unzählige Male in der Kern- und Elementarteilchenphysik experimentell bestätigt. Siehe beispielsweise Positronen-Elektronen-Paar-Produktion oder Energieeinsparung bei Kernreaktionen .
Siehe auch: Relativistische Masse
Beispiel: Protons kinetische Energie
Ein Proton ( m = 1,67 × 10 –27 kg ) bewegt sich mit einer Geschwindigkeit v = 0,9900 c = 2,968 × 10 8 m / s . Was ist seine kinetische Energie ?
Nach einer klassischen Berechnung, die nicht korrekt ist, würden wir erhalten:
K = 1 / 2mv 2 = ½ x (1,67 x 10 -27 kg) x (2,968 x 10 8 m / s) 2 = 7,355 x 10 -11 J.
Bei der relativistischen Korrektur ist die relativistische kinetische Energie gleich:
K = (ɣ – 1) mc 2
wo der Lorentz-Faktor
ɣ = 7,089
deshalb
K = 6,089 × (1,67 × 10 –27 kg) × (2,9979 × 10 8 m / s) 2 = 9,139 × 10 –10 J = 5,701 GeV
Dies ist etwa 12-mal höhere Energie als bei der klassischen Berechnung. Entsprechend dieser Beziehung erfordert eine Beschleunigung eines Protonenstrahls auf 5,7 GeV Energien, die in der Größenordnung unterschiedlich sind.
……………………………………………………………………………………………………………………………….
Dieser Artikel basiert auf der maschinellen Übersetzung des englischen Originalartikels. Weitere Informationen finden Sie im Artikel auf Englisch. Sie können uns helfen. Wenn Sie die Übersetzung korrigieren möchten, senden Sie diese bitte an: translations@nuclear-power.com oder füllen Sie das Online-Übersetzungsformular aus. Wir bedanken uns für Ihre Hilfe und werden die Übersetzung so schnell wie möglich aktualisieren. Danke.
