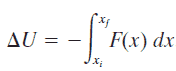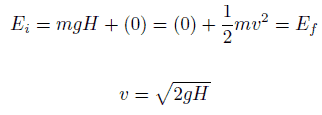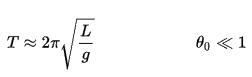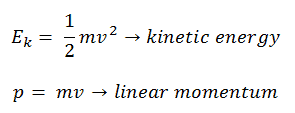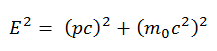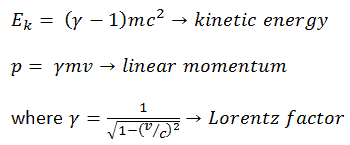L’énergie cinétique, K, est définie comme l’énergie stockée dans un objet en raison de son mouvement. Il est appelé énergie cinétique, du mot grec kinetikos – mouvement. Génie thermique
Qu’est-ce que l’énergie cinétique
L’énergie cinétique, K , est définie comme l’énergie stockée dans un objet en raison de son mouvement. Un objet en mouvement a la capacité de travailler et peut donc être considéré comme ayant de l’énergie. On l’appelle énergie cinétique, du mot grec kinetikos, qui signifie «mouvement».
L’ énergie cinétique dépend de la vitesse d’un objet et est la capacité d’un objet en mouvement à travailler sur d’autres objets lorsqu’il entre en collision avec eux. D’autre part, l’énergie cinétique d’un objet représente la quantité d’énergie nécessaire pour augmenter la vitesse de l’objet du repos (v = 0) à sa vitesse finale. L’énergie cinétique dépend également linéairement de la masse, qui est une mesure numérique de l’ inertie d’un objet et la mesure de la résistance d’un objet à l’accélération lorsqu’une force est appliquée.
Nous définissons la quantité:
K = ½ mv 2
être l’ énergie cinétique de translation de l’objet. Il faut l’ajouter, on l’appelle l’énergie cinétique «translationnelle» pour la distinguer de l’énergie cinétique rotationnelle.
Conservation de l’énergie mécanique
Le principe de la conservation de l’énergie mécanique a d’abord été énoncé:
L’énergie mécanique totale (définie comme la somme de ses énergies potentielles et cinétiques) d’une particule sur laquelle agissent uniquement les forces conservatrices est constante .
Voir aussi: Conservation de l’énergie mécanique
Un système isolé est un système dans lequel aucune force externe ne provoque de changements d’énergie. Si seules les forces conservatrices agissent sur un objet et U est la fonction d’ énergie potentielle pour la force conservatrice totale, alors
E mech = U + K
L’énergie potentielle, U , dépend de la position d’un objet soumis à une force conservatrice.
Elle est définie comme la capacité de l’objet à travailler et est augmentée lorsque l’objet est déplacé dans la direction opposée à la direction de la force.
L’énergie potentielle associée à un système composé de la Terre et d’une particule voisine est l’énergie potentielle gravitationnelle .
L’énergie cinétique, K , dépend de la vitesse d’un objet et est la capacité d’un objet en mouvement à travailler sur d’autres objets lorsqu’il entre en collision avec eux.
K = ½ mv 2
La définition mentionnée ci-dessus ( E mech = U + K ) suppose que le système est exempt de frottement et d’autres forces non conservatrices . La différence entre une force conservatrice et une force non conservatrice est que lorsqu’une force conservatrice déplace un objet d’un point à un autre, le travail effectué par la force conservatrice est indépendant du chemin.
Dans toute situation réelle, des forces de friction et d’autres forces non conservatrices sont présentes, mais dans de nombreux cas, leurs effets sur le système sont si faibles que le principe de conservation de l’énergie mécanique peut être utilisé comme une approximation juste. Par exemple, la force de friction est une force non conservatrice, car elle agit pour réduire l’énergie mécanique dans un système.
Notez que les forces non conservatrices ne réduisent pas toujours l’énergie mécanique. Une force non conservatrice modifie l’énergie mécanique, il existe des forces qui augmentent l’énergie mécanique totale, comme la force fournie par un moteur ou un moteur, est également une force non conservatrice.
Bloc glissant sur une pente inclinée sans friction
Le bloc de 1 kg commence à une hauteur H (disons 1 m) au-dessus du sol, avec une énergie potentielle mgH et une énergie cinétique égale à 0. Il glisse vers le sol (sans frottement) et arrive sans énergie potentielle et énergie cinétique K = ½ mv 2 . Calculez la vitesse du bloc au sol et son énergie cinétique.
E mech = U + K = const
=> ½ mv 2 = mgH
=> v = √2gH = 4,43 m / s
=> K 2 = ½ x 1 kg x (4,43 m / s) 2 = 19,62 kg.m 2 .s -2 = 19,62 J
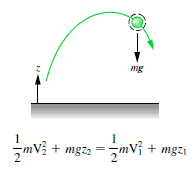
Pendule
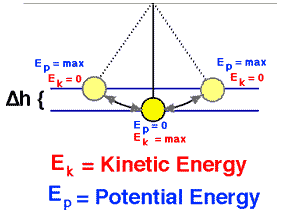Supposons un pendule (boule de masse m suspendue à une chaîne de longueur L que nous avons tirée de sorte que la balle soit à une hauteur H <L au-dessus de son point le plus bas sur l’arc de son mouvement de corde tendue. Le pendule est soumis au conservateur force gravitationnelle où les forces de friction comme la traînée d’air et la friction au pivot sont négligeables.
Nous le libérons du repos. À quelle vitesse va-t-il au fond?
Le pendule atteint la plus grande énergie cinétique et le moins d’énergie potentielle lorsqu’il est en position verticale , car il aura la plus grande vitesse et sera le plus proche de la Terre à ce point. D’un autre côté, il aura sa moindre énergie cinétique et sa plus grande énergie potentielle aux positions extrêmes de son swing, car il a une vitesse nulle et est le plus éloigné de la Terre en ces points.
Si l’amplitude est limitée à de petites oscillations, la période T d’un simple pendule, le temps pris pour un cycle complet, est:
où L est la longueur du pendule et g est l’accélération locale de la gravité. Pour les petites balançoires, la période de balancement est approximativement la même pour les balançoires de tailles différentes. Autrement dit, la période est indépendante de l’amplitude .
Énergie cinétique relativiste
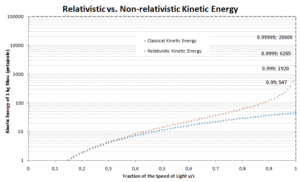
La relation précédente entre le travail et l’énergie cinétique est basée sur les lois du mouvement de Newton . Lorsque nous généralisons ces lois selon le principe de la relativité, nous avons besoin d’une généralisation correspondante de l’équation de l’énergie cinétique . Si la vitesse d’un objet est proche de la vitesse de la lumière, il est nécessaire d’utiliser la mécanique relativiste pour calculer son énergie cinétique .
En mécanique classique , l’énergie cinétique et l’élan sont exprimés comme:
La dérivation de ses relations relativistes est basée sur la relation relativiste énergie-momentum:
Elle peut être dérivée, l’ énergie cinétique relativiste et la quantité de mouvement relativiste sont:
Le premier terme ( ɣmc 2 ) de l’ énergie cinétique relativiste augmente avec la vitesse v de la particule. Le deuxième terme ( mc 2 ) est constant; elle est appelée énergie de repos (masse au repos) de la particule et représente une forme d’énergie qu’une particule possède même lorsqu’elle est à vitesse nulle . Lorsque la vitesse d’un objet s’approche de la vitesse de la lumière, l’ énergie cinétique s’approche de l’infini . Elle est causée par le facteur de Lorentz , qui se rapproche de l’infini pour v → c . Par conséquent, la vitesse de la lumière ne peut être atteinte par aucune particule massive.
Le premier terme (ɣmc 2 ) est connu comme l’ énergie totale E de la particule, car il est égal à l’énergie de repos plus l’énergie cinétique:
E = K + mc 2
Pour une particule au repos, c’est-à-dire que K est nul, l’énergie totale est donc son énergie de repos:
E = mc 2
C’est l’un des résultats frappants de la théorie de la relativité d’Einstein : la masse et l’énergie sont équivalentes et convertibles l’ une dans l’autre. L’équivalence de la masse et de l’énergie est décrite par la célèbre formule d’Einstein E = mc 2 . Ce résultat a été confirmé à maintes reprises expérimentalement en physique nucléaire et élémentaire des particules. Par exemple, voir Production de paires positrons-électrons ou Conservation de l’énergie dans les réactions nucléaires .
Voir aussi: Messe relativiste
Exemple: énergie cinétique du proton
Un proton ( m = 1,67 x 10 -27 kg ) se déplace à une vitesse v = 0,9900c = 2,968 x 10 8 m / s . Quelle est son énergie cinétique ?
Selon un calcul classique, qui n’est pas correct, on obtiendrait:
K = 1 / 2mv 2 = ½ x (1,67 x 10 -27 kg) x (2,968 x 10 8 m / s) 2 = 7,355 x 10 -11 J
Avec la correction relativiste, l’énergie cinétique relativiste est égale à:
K = (ɣ – 1) mc 2
où le facteur de Lorentz
ɣ = 7,089
par conséquent
K = 6,089 x (1,67 x 10 -27 kg) x (2,9979 x 10 8 m / s) 2 = 9,139 x 10 -10 J = 5,701 GeV
C’est environ 12 fois plus d’ énergie que dans le calcul classique. Selon cette relation, une accélération d’un faisceau de protons à 5,7 GeV nécessite des énergies qui sont dans l’ordre différent.
……………………………………………………………………………………………………………………………….
Cet article est basé sur la traduction automatique de l’article original en anglais. Pour plus d’informations, voir l’article en anglais. Pouvez vous nous aider Si vous souhaitez corriger la traduction, envoyez-la à l’adresse: translations@nuclear-power.com ou remplissez le formulaire de traduction en ligne. Nous apprécions votre aide, nous mettrons à jour la traduction le plus rapidement possible. Merci
