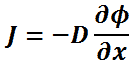Quel est le nombre de Péclet – Définition

Quel est le nombre de Péclet

Le nombre de Péclet est un nombre sans dimension, du nom du physicien français Jean Claude Eugène Péclet. Le nombre de Péclet  est défini comme le rapport entre le taux d’advection d’une quantité physique par le flux et le taux de diffusion (matière ou chaleur) de la même quantité entraînée par un gradient approprié. Par conséquent, nous devons distinguer le nombre de Peclet pour le transfert de masse et le transfert de chaleur.

Nombre de peclet dans le transfert de masse

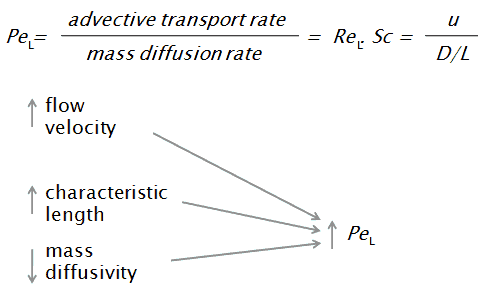
Dans les problèmes de transfert de masse, le nombre de Péclet est le produit du nombre de Reynolds , qui décrit le  régime d’écoulement , et du nombre de Schmidt , utilisé pour caractériser les écoulements de fluides dans lesquels il existe des processus de convection simultanés par impulsion et par diffusion massive.

où:

• u  est la vitesse d’écoulement,
• L  est une  dimension linéaire caractéristique (longueur parcourue du fluide;  diamètre hydraulique,  etc.)
• D est la diffusivité de masse [m ² / s]

Nombre de peclet dans le transfert de chaleur

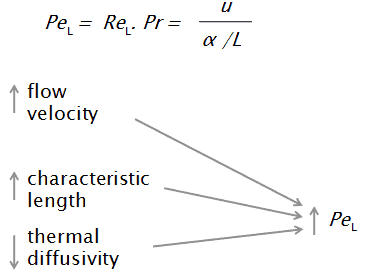
Dans les problèmes de transfert de chaleur, le nombre de Péclet est le rapport de l’énergie thermique convectée au fluide à l’énergie thermique conduite dans le fluide. Le  nombre de Péclet  est simplement défini comme le produit du nombre de Reynolds , qui décrit le régime d’écoulement , et du  nombre de Prandtl , qui décrit la relation entre la diffusivité du moment et la diffusivité thermique. Si Pe est petit, la conduction est importante.

où:

• u  est la vitesse d’écoulement,
• L  est une  dimension linéaire caractéristique , (longueur parcourue du fluide;  diamètre hydraulique,  etc.)
• α  est  la diffusivité thermique  [m ² / s]

La diffusivité thermique représente la vitesse à laquelle la chaleur diffuse à travers un matériau et a des unités m ² / s. En d’autres termes, c’est la mesure de l’  inertie thermique  d’un matériau donné. La diffusivité thermique est généralement notée α et est donnée par:

Comme on peut le voir, il mesure la capacité d’un matériau à conduire l’  énergie thermique (représentée par le facteur k) par rapport à sa capacité à stocker l’énergie thermique (représentée par le facteur ρ.c _p ). Les matériaux de grand α répondront rapidement aux changements de leur environnement thermique, tandis que les matériaux de petit α répondront plus lentement (la chaleur est principalement absorbée), en prenant plus de temps pour atteindre une nouvelle condition d’équilibre.

Diffusivité de masse et loi de Fick

La diffusivité est rencontrée dans la loi de Fick, qui stipule:

Si la concentration d’un soluté dans une région est supérieure à celle d’une autre solution, le soluté diffuse de la région de concentration plus élevée à la région de concentration plus faible, avec une ampleur proportionnelle au gradient de concentration.

Dans une dimension (spatiale), la loi est:

où:

• J est le flux de diffusion,
• D est le coefficient de diffusion,
• φ (pour les mélanges idéaux) est la concentration.

L’utilisation de cette loi dans la théorie des réacteurs nucléaires conduit à l’ approximation de diffusion .