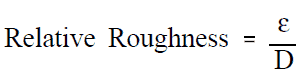Perte de tête majeure – Perte par friction
Les pertes importantes , qui sont associées à la perte d’énergie de frottement par longueur de tuyau, dépendent de la vitesse d’écoulement, de la longueur du tuyau, du diamètre du tuyau et d’un facteur de friction basé sur la rugosité du tuyau, et si le débit est laminaire ou turbulent (c.-à-d. Le Reynolds numéro du flux).
Bien que la perte de charge représente une perte d’énergie , elle ne représente pas une perte d’énergie totale du fluide. L’énergie totale du fluide se conserve grâce à la loi de conservation de l’énergie . En réalité, la perte de charge due au frottement se traduit par une augmentation équivalente de l’énergie interne (augmentation de la température) du fluide.
Par observation, la perte de charge principale est à peu près proportionnelle au carré du débit dans la plupart des écoulements d’ingénierie (écoulement turbulent entièrement développé).
L’équation la plus couramment utilisée pour calculer les pertes de charge importantes dans un tube ou un conduit est l’ équation de Darcy – Weisbach .
Équation de Darcy-Weisbach
En dynamique des fluides, l’équation de Darcy-Weisbach est une équation phénoménologique, qui relie la perte de charge principale , ou perte de pression, due au frottement du fluide le long d’une longueur donnée de tuyau à la vitesse moyenne. Cette équation est valable pour un écoulement monophasique complètement développé, stable et incompressible .
L’équation de Darcy – Weisbach peut être écrite sous deux formes ( forme de perte de pression ou forme de perte de charge ). Dans le formulaire de perte de tête peut s’écrire:
où:
- Δh = la perte de charge due au frottement (m)
- f D = le facteur de friction Darcy (sans unité)
- L = la longueur du tuyau (m)
- D = le diamètre hydraulique du tuyau D (m)
- g = la constante gravitationnelle (m / s 2 )
- V = la vitesse d’écoulement moyenne V (m / s)
Sommaire:
- La perte de charge du système hydraulique est divisée en deux catégories principales :
- Perte de charge importante – due au frottement dans des tuyaux droits
- Perte de charge mineure – due à des composants comme des valves, des coudes…
- L’équation de Darcy peut être utilisée pour calculer les pertes majeures .
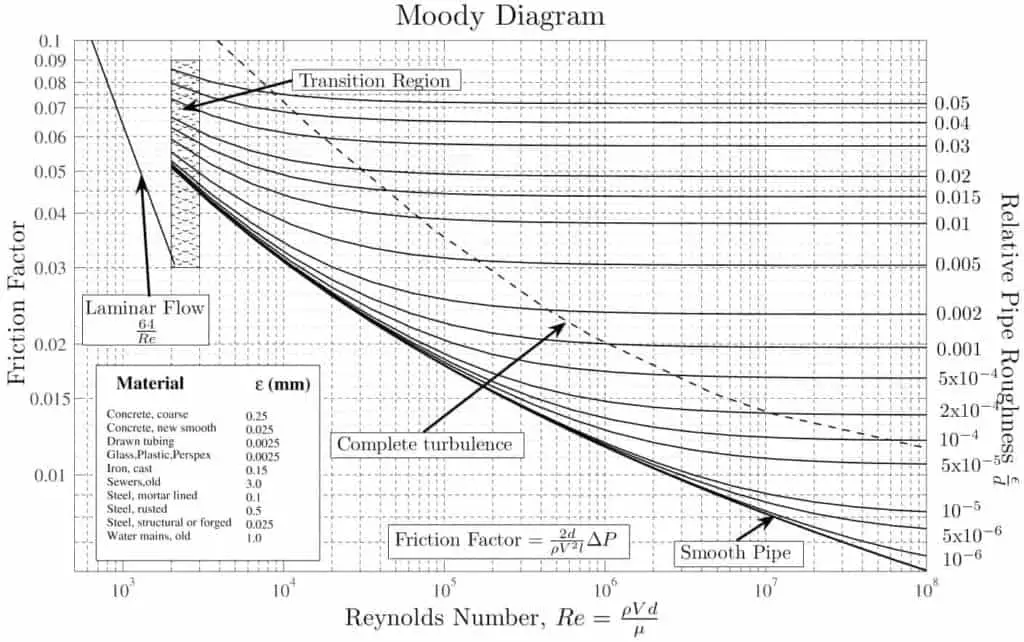
- Le facteur de friction pour l’écoulement du fluide peut être déterminé à l’aide d’un diagramme de Moody .
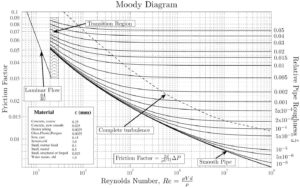
- Le facteur de friction pour l’écoulement laminaire est indépendant de la rugosité de la surface intérieure du tuyau. f = 64 / Re
- Le facteur de frottement pour un écoulement turbulent dépend fortement de la rugosité relative. Elle est déterminée par l’équation de Colebrook. Il faut noter qu’aux très grands nombres de Reynolds , le facteur de friction est indépendant du nombre de Reynolds.
Pourquoi la perte de tête est très importante?
Comme on peut le voir sur la photo, la perte de charge est une caractéristique clé de tout système hydraulique. Dans les systèmes dans lesquels un certain débit doit être maintenu (par exemple pour assurer un refroidissement ou un transfert de chaleur suffisant à partir d’un cœur de réacteur ), l’équilibre de la perte de charge et de la tête ajoutée par une pompe détermine le débit à travers le système.
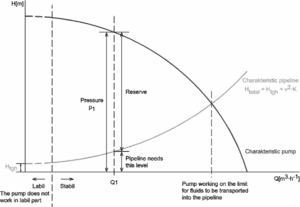
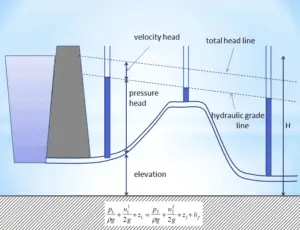
L’évaluation de l’ équation de Darcy-Weisbach donne un aperçu des facteurs affectant la perte de charge dans un pipeline.
- Considérez que la longueur du tuyau ou du canal est doublée , la perte de charge par friction qui en résulte doublera .
- À débit et longueur de tuyau constants, la perte de charge est inversement proportionnelle à la 4e puissance de diamètre (pour un flux laminaire), et donc la réduction de moitié du diamètre du tuyau augmente la perte de charge d’un facteur 16. Il s’agit d’une augmentation très significative de perte de charge et montre pourquoi des tuyaux de plus grand diamètre entraînent des besoins en puissance de pompage beaucoup plus faibles.
- Puisque la perte de charge est à peu près proportionnelle au carré du débit, alors si le débit est doublé , la perte de charge augmente d’un facteur quatre .
- La perte de charge est réduite de moitié (pour un flux laminaire) lorsque la viscosité du fluide est réduite de moitié .
https://commons.wikimedia.org/w/index.php?curid=4681366
À l’exception du facteur de friction Darcy , chacun de ces termes (la vitesse d’écoulement, le diamètre hydraulique , la longueur d’un tuyau) peut être facilement mesuré. Le facteur de friction Darcy prend en compte les propriétés fluides de la densité et de la viscosité, ainsi que la rugosité du tuyau . Ce facteur peut être évalué par l’utilisation de diverses relations empiriques, ou il peut être lu à partir de graphiques publiés (par exemple graphique Moody ).
Facteur de friction Darcy
Il existe deux facteurs de friction courants, le Darcy et le Fanning .
Le facteur de friction de Darcy est une grandeur sans dimension utilisée dans l’équation de Darcy – Weisbach, pour la description des pertes par friction dans les tuyaux ou les conduits ainsi que pour l’écoulement en canal ouvert. C’est ce qu’on appelle également le facteur de friction Darcy – Weisbach , le coefficient de résistance ou simplement le facteur de friction .Il a été déterminé que le facteur de friction dépend du nombre de Reynolds pour le débit et du degré de rugosité de la surface intérieure du tuyau (en particulier pour un écoulement turbulent ). Le facteur de friction de l’écoulement laminaire est indépendant de la rugosité de la surface intérieure du tuyau.
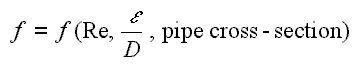
La section transversale du tuyau est également importante, car les écarts par rapport à la section circulaire provoqueront des écoulements secondaires qui augmenteront la perte de charge. Les tuyaux et conduits non circulaires sont généralement traités en utilisant le diamètre hydraulique .
Rugosité relative
La quantité utilisée pour mesurer la rugosité de la surface intérieure du tuyau est appelée rugosité relative , et elle est égale à la hauteur moyenne des irrégularités de surface (ε) divisée par le diamètre du tuyau (D).
, où les irrégularités de surface de hauteur moyenne et le diamètre du tuyau sont exprimés en millimètres.
Si nous connaissons la rugosité relative de la surface intérieure du tuyau, nous pouvons obtenir la valeur du facteur de friction à partir du diagramme de Moody .
Le diagramme de Moody (également connu sous le nom de diagramme de Moody) est un graphique sous forme non dimensionnelle qui met en relation le facteur de friction Darcy , le nombre de Reynolds et la rugosité relative pour un écoulement pleinement développé dans un tuyau circulaire.
Facteur de friction de Darcy pour divers régimes d’écoulement
La classification la plus courante des régimes d’écoulement est basée sur le nombre de Reynolds. Le nombre de Reynolds est un nombre sans dimension comprenant les caractéristiques physiques de l’écoulement et il détermine si l’écoulement est laminaire ou turbulent . Un nombre de Reynolds croissant indique une turbulence croissante de l’écoulement. Comme le montre le graphique de Moody, le facteur de friction de Darcy dépend également fortement du régime d’écoulement (c’est-à-dire du nombre de Reynolds).
……………………………………………………………………………………………………………………………….
Cet article est basé sur la traduction automatique de l’article original en anglais. Pour plus d’informations, voir l’article en anglais. Pouvez vous nous aider Si vous souhaitez corriger la traduction, envoyez-la à l’adresse: translations@nuclear-power.com ou remplissez le formulaire de traduction en ligne. Nous apprécions votre aide, nous mettrons à jour la traduction le plus rapidement possible. Merci