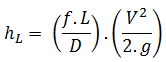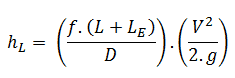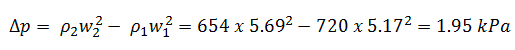Les pertes de charge mineures sont des pertes de charge locales ou des chutes de pression de divers éléments hydrauliques tels que des coudes, des raccords, des vannes, des coudes, des tés ou des canaux chauffants. Génie thermique
Perte de tête mineure – Pertes locales
Dans l’industrie, tout système de tuyauterie contient différents éléments technologiques tels que des coudes, des raccords, des vannes ou des canaux chauffants . Ces composants supplémentaires augmentent la perte de charge globale du système. Ces pertes sont généralement appelées pertes mineures , bien qu’elles représentent souvent une part importante de la perte de charge . Pour les systèmes de tuyaux relativement courts, avec un nombre relativement important de coudes et de raccords, les pertes mineures peuvent facilement dépasser les pertes majeures (en particulier avec une vanne partiellement fermée qui peut provoquer une perte de pression plus importante qu’un long tuyau, en fait quand une vanne est fermée ou presque fermée, la perte mineure est infinie).
Les pertes mineures sont généralement mesurées expérimentalement. Les données, en particulier pour les vannes, dépendent quelque peu de la conception particulière du fabricant.
Tout comme le frottement des tuyaux, les pertes mineures sont à peu près proportionnelles au carré du débit et peuvent donc être facilement intégrées dans l’ équation de Darcy-Weisbach . K est la somme de tous les coefficients de perte dans la longueur du tuyau, chacun contribuant à la perte de charge globale.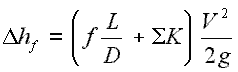
Il existe plusieurs méthodes pour calculer la perte de charge des raccords, des coudes et des coudes. Dans la section suivante, ces méthodes sont résumées dans l’ordre du plus simple au plus sophistiqué.
Méthode de longueur équivalente
La méthode de longueur équivalente ( méthode L e / D ) permet à l’utilisateur de décrire la perte de pression à travers un coude ou un raccord comme une longueur de tuyau droit .
Cette méthode est basée sur l’observation que les pertes importantes sont également proportionnelles à la tête de vitesse ( v 2 / 2g ).
La méthode L e / D augmente simplement le facteur multiplicateur dans l’ équation de Darcy-Weisbach (c’est-à-dire ƒ.L / D ) par une longueur de tuyau droit (c’est-à-dire L e ) qui donnerait lieu à une perte de pression équivalente aux pertes dans le raccords, d’où le nom de «longueur équivalente». Le facteur multiplicateur devient donc ƒ (L + L e ) / D et l’équation pour le calcul de la perte de charge du système est donc:
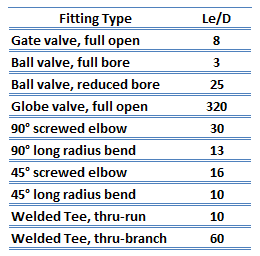 Tous les raccords, coudes, tés peuvent être additionnés pour faire une longueur totale et la perte de pression calculée à partir de cette longueur. Il a été constaté expérimentalement que si les longueurs équivalentes pour une gamme de tailles d’un type donné de raccord sont divisées par les diamètres des raccords, alors un rapport presque constant (c’est-à-dire L e / D) est obtenu. L’avantage de la méthode de longueur équivalente est qu’une seule valeur de données est suffisante pour couvrir toutes les tailles de cet ajustement et donc la tabulation de données de longueur équivalente est relativement facile. Certaines longueurs équivalentes typiques sont indiquées dans le tableau.Voir aussi: Logiciel de dimensionnement de tuyaux et de calcul de débit
Tous les raccords, coudes, tés peuvent être additionnés pour faire une longueur totale et la perte de pression calculée à partir de cette longueur. Il a été constaté expérimentalement que si les longueurs équivalentes pour une gamme de tailles d’un type donné de raccord sont divisées par les diamètres des raccords, alors un rapport presque constant (c’est-à-dire L e / D) est obtenu. L’avantage de la méthode de longueur équivalente est qu’une seule valeur de données est suffisante pour couvrir toutes les tailles de cet ajustement et donc la tabulation de données de longueur équivalente est relativement facile. Certaines longueurs équivalentes typiques sont indiquées dans le tableau.Voir aussi: Logiciel de dimensionnement de tuyaux et de calcul de débit
Méthode du coefficient de résistance – Méthode K – Tête excédentaire
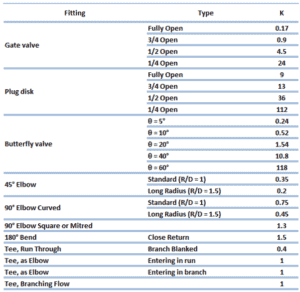 La méthode de coefficient de résistance (ou K-procédé, ou procédé de tête en excès) permet à l’utilisateur de décrire la chute de pression à travers un coude ou un raccord par un numéro de dimension – K . Ce nombre sans dimension (K) peut être incorporé dans l’ équation de Darcy-Weisbach d’une manière très similaire à la méthode de la longueur équivalente. Au lieu de données de longueur équivalente dans ce cas, le nombre sans dimension (K) est utilisé pour caractériser le raccord sans le lier aux propriétés du tuyau.
La méthode de coefficient de résistance (ou K-procédé, ou procédé de tête en excès) permet à l’utilisateur de décrire la chute de pression à travers un coude ou un raccord par un numéro de dimension – K . Ce nombre sans dimension (K) peut être incorporé dans l’ équation de Darcy-Weisbach d’une manière très similaire à la méthode de la longueur équivalente. Au lieu de données de longueur équivalente dans ce cas, le nombre sans dimension (K) est utilisé pour caractériser le raccord sans le lier aux propriétés du tuyau.
La valeur K représente le multiple des têtes de vitesse qui seront perdues par le fluide traversant le raccord. L’équation de calcul de la perte de charge de l’élément hydraulique est donc:
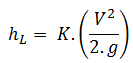 Par conséquent, l’équation pour le calcul de la perte de pression de l’ensemble du système hydraulique est:
Par conséquent, l’équation pour le calcul de la perte de pression de l’ensemble du système hydraulique est:
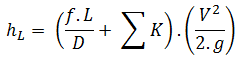
La valeur K peut être caractérisée pour différents régimes d’écoulement (c’est-à-dire selon le nombre de Reynolds ), ce qui la rend plus précise que la méthode de la longueur équivalente.
Il existe plusieurs autres méthodes pour calculer la perte de pression des raccords, ces méthodes sont plus sophistiquées et également plus précises :
- Méthode 2K . La méthode 2K est une technique développée par Hooper BW pour prédire la perte de charge dans un coude, une valve ou un té. La méthode 2K améliore la méthode de la tête excédentaire en caractérisant la variation de la perte de pression due à la variation du nombre de Reynolds . La méthode 2-K est avantageuse par rapport à une autre méthode, en particulier dans la région d’écoulement laminaire .
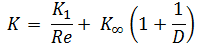
- Méthode 3K . La méthode 3K (par Ron Darby en 1999) améliore encore la précision du calcul de la perte de pression en caractérisant également le changement des proportions géométriques d’un raccord à mesure que sa taille change. Cela rend la méthode 3K particulièrement précise pour un système avec de grands raccords .
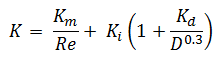
Sommaire:
- La perte de charge du système hydraulique est divisée en deux catégories principales :
- Perte de charge importante – due au frottement dans des tuyaux droits
- Perte de charge mineure – due à des composants comme des valves, des coudes…
- Une forme spéciale de l’équation de Darcy peut être utilisée pour calculer les pertes mineures .
- Les pertes mineures sont à peu près proportionnelle à la place du débit et par conséquent , ils peuvent être intégrés facilement dans l’équation de Darcy-Weisbach par coefficient de résistance K .
- En tant que perte de pression locale, l’accélération du fluide dans un canal chauffé peut également être envisagée.
Il existe les méthodes suivantes:
- Méthode de longueur équivalente
- Méthode K (méthode du coefficient de résistance)
- Méthode 2K
- Méthode 3K
Pourquoi la perte de tête est très importante?
Comme on peut le voir sur la photo, la perte de charge est une caractéristique clé de tout système hydraulique. Dans les systèmes dans lesquels un certain débit doit être maintenu (par exemple pour assurer un refroidissement ou un transfert de chaleur suffisant à partir d’un cœur de réacteur ), l’équilibre de la perte de charge et de la tête ajoutée par une pompe détermine le débit à travers le système.
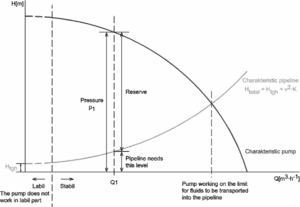
Écoulement à travers le coude – perte mineure
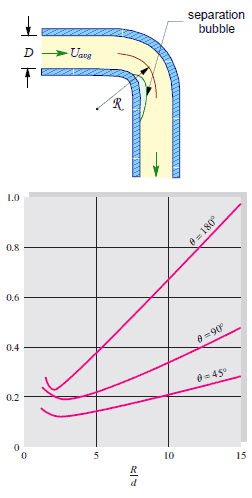 L’écoulement à travers les coudes est assez compliqué . En fait, tout tuyau courbe induit toujours une perte plus importante que le simple tuyau droit. Cela est dû au fait que dans un tuyau courbe, le flux se sépare sur les parois courbes. Pour un très petit rayon de courbure, le flux entrant est même incapable de faire le virage au coude, donc le flux se sépare et stagne en partie contre le côté opposé du tuyau. Dans cette partie du virage, la pression augmente (en raison du principe de Bernoulli ) et la vitesse diminue.
L’écoulement à travers les coudes est assez compliqué . En fait, tout tuyau courbe induit toujours une perte plus importante que le simple tuyau droit. Cela est dû au fait que dans un tuyau courbe, le flux se sépare sur les parois courbes. Pour un très petit rayon de courbure, le flux entrant est même incapable de faire le virage au coude, donc le flux se sépare et stagne en partie contre le côté opposé du tuyau. Dans cette partie du virage, la pression augmente (en raison du principe de Bernoulli ) et la vitesse diminue.
Une caractéristique intéressante des valeurs K pour les coudes est leur comportement non monotone lorsque le rapport R / D augmente. Les valeurs K incluent à la fois les pertes locales et les pertes par frottement du tuyau. Les pertes locales, causées par la séparation des flux et le flux secondaire, diminuent avec R / D, tandis que les pertes par frottement augmentent car la longueur de pliage augmente. Par conséquent, il y a un minimum dans la valeur K près du rayon de courbure normalisé de 3.
Accélération fluide
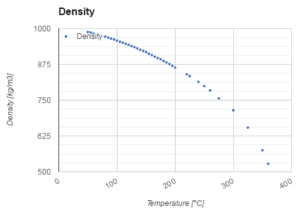
Il est connu que lorsque le fluide est chauffé (par exemple dans un canal de carburant), le fluide se dilate (modification de la densité du fluide) et augmente sa vitesse d’écoulement en raison de l’ équation de continuité (la section transversale du canal reste la même). Pour un volume de contrôle qui a une seule entrée et une seule sortie, cette équation indique que, pour un débit en régime permanent, le débit massique dans le volume doit être égal au débit massique sortant.
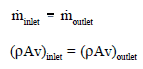
Masse entrant par unité de temps = Masse sortant par unité de temps
Voir aussi: Propriétés de l’eau sous-refroidie
Un autre principe très important stipule ( le principe de Bernoulli ) que l’ augmentation de la vitesse d’écoulement dans le canal chauffé provoque l’ abaissement de la pression du fluide . Cette perte de pression peut également être considérée comme une perte de pression locale et peut être calculée à partir de l’équation suivante:
![]()
Débit à travers un cœur de réacteur – accélération du liquide de refroidissement
Il s’agit d’un exemple illustratif, les données suivantes ne correspondent à aucune conception de réacteur.

Les réacteurs à eau sous pression sont refroidis et modérés par de l’eau liquide à haute pression (par exemple 16 MPa). À cette pression, l’eau bout à environ 350 ° C (662 ° F). La température d’entrée de l’eau est d’environ 290 ° C (⍴ ~ 720 kg / m 3 ). L’eau (liquide de refroidissement) est chauffée dans le cœur du réacteur à environ 325 ° C (65 ~ 654 kg / m 3 ) lorsque l’eau s’écoule à travers le cœur.
Le circuit primaire des REP typiques est divisé en 4 boucles indépendantes (diamètre de la tuyauterie ~ 700 mm), chaque boucle comprend un générateur de vapeur et une pompe de refroidissement principale . À l’intérieur de la cuve du réacteur (RPV), le liquide de refroidissement descend d’abord à l’extérieur du cœur du réacteur (à travers le tuyau de descente). Depuis le fond de l’enceinte sous pression, le flux est inversé à travers le cœur, où la température du liquide de refroidissement augmente lors de son passage à travers les crayons combustibles et les assemblages formés par eux.
Calculer:
- Perte de pression due à l’ accélération du liquide de refroidissement dans un canal de carburant isolé
quand
- la vitesse d’écoulement à l’ entrée du canal est égale à 5,17 m / s
- la vitesse d’écoulement de sortie du canal est égale à 5,69 m / s
Solution:
La perte de charge due à l’accélération du liquide de refroidissement dans un canal de carburant isolé est alors:
Ce fait a des conséquences importantes. En raison de la puissance relative différente des assemblages combustibles dans un cœur, ces assemblages combustibles ont une résistance hydraulique différente , ce qui peut induire un écoulement latéral local du liquide de refroidissement primaire et cela doit être pris en compte dans les calculs thermo-hydrauliques.
……………………………………………………………………………………………………………………………….
Cet article est basé sur la traduction automatique de l’article original en anglais. Pour plus d’informations, voir l’article en anglais. Pouvez vous nous aider Si vous souhaitez corriger la traduction, envoyez-la à l’adresse: translations@nuclear-power.com ou remplissez le formulaire de traduction en ligne. Nous apprécions votre aide, nous mettrons à jour la traduction le plus rapidement possible. Merci