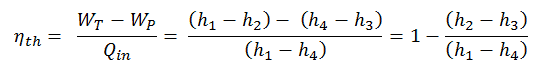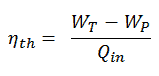Cycle de Rankine – Cycle de turbine à vapeur
En 1859, un ingénieur écossais, William John Macquorn Rankine a fait progresser l’étude des moteurs thermiques en publiant le « Manuel de la machine à vapeur et autres moteurs principaux ». Rankine a développé une théorie complète de la machine à vapeur et de tous les moteurs thermiques. Avec Rudolf Clausius et William Thomson (Lord Kelvin), il a contribué à la thermodynamique, se concentrant particulièrement sur la première des trois lois thermodynamiques.
Le cycle de Rankine a été nommé d’après lui et décrit les performances des systèmes de turbines à vapeur , bien que le principe théorique s’applique également aux moteurs alternatifs tels que les locomotives à vapeur. En général, le cycle de Rankine est un cycle thermodynamique idéalisé d’un moteur thermique à pression constante qui convertit une partie de la chaleur en travail mécanique. Dans ce cycle, la chaleur est fournie de l’extérieur à une boucle fermée, qui utilise généralement de l’eau (en phase liquide et vapeur) comme fluide de travail. Contrairement au cycle de Brayton , le fluide de travail du cycle de Rankine subit le changement de phase d’une phase liquide à une phase vapeur et vice versa.
Alors que de nombreuses substances pourraient être utilisées comme fluide de travail dans le cycle de Rankine (inorganiques ou même organiques), l’ eau est généralement le fluide de choix en raison de ses propriétés favorables, telles que sa chimie non toxique et non réactive, son abondance et son faible coût, ainsi que ses propriétés thermodynamiques. Par exemple, l’ eau a la plus haute chaleur spécifique d’une substance commune – 4,19 kJ / kg K. De plus , il a très forte chaleur de vaporisation , ce qui en fait un refroidissement efficace et moyenne dans les centrales thermiques et autres industrie de l’ énergie. Dans le cas du cycle de Rankine, la loi des gaz parfaitspresque ne peut pas être utilisé (la vapeur ne suit pas pV = nRT), donc tous les paramètres importants de l’eau et de la vapeur sont tabulés dans ce que l’on appelle des « tableaux de vapeur ».
L’un des principaux avantages du cycle de Rankine est que le processus de compression dans la pompe a lieu sur un liquide . En condensant la vapeur de travail à un liquide (à l’intérieur d’un condenseur), la pression à la sortie de la turbine est abaissée et l’énergie requise par la pompe d’alimentation ne consomme que 1% à 3% de la puissance de sortie de la turbine et ces facteurs contribuent à une plus grande efficacité pour le cycle.
Étant donné que le principe de Carnot stipule qu’aucun moteur ne peut être plus efficace qu’un moteur réversible ( un moteur thermique Carnot ) fonctionnant entre les mêmes réservoirs haute température et basse température, une turbine à vapeur basée sur le cycle de Rankine doit avoir une efficacité inférieure à l’efficacité Carnot.
Dans les centrales nucléaires modernes , le rendement thermique global est d’environ un tiers (33%), de sorte que 3000 MWth d’énergie thermique provenant de la réaction de fission sont nécessaires pour générer 1000 MWe d’énergie électrique. Des rendements plus élevés peuvent être atteints en augmentant la température de la vapeur . Mais cela nécessite une augmentation des pressions à l’intérieur des chaudières ou des générateurs de vapeur. Cependant, des considérations métallurgiques imposent des limites supérieures à ces pressions. Par rapport à d’autres sources d’énergie, le rendement thermique de 33% n’est pas beaucoup. Mais il faut noter que les centrales nucléaires sont beaucoup plus complexes que les centrales à combustibles fossiles et qu’il est beaucoup plus facile de brûler des combustibles fossiles que de produire de l’énergie à partir de combustibles nucléaires .
Cycle de Rankine – Processus
Dans un cycle de Rankine idéal, le système exécutant le cycle subit une série de quatre processus: deux processus isentropiques (adiabatiques réversibles) alternés avec deux processus isobares:
-
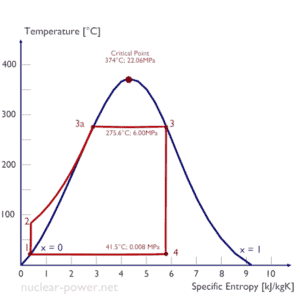
Cycle de Rankine – Diagramme Ts Compression isentropique (compression dans les pompes centrifuges) – Le condensat liquide est comprimé adiabatiquement de l’état 1 à l’état 2 par des pompes centrifuges (généralement par des pompes à condensats puis par des pompes à eau d’alimentation). Les condensats liquides sont pompés du condenseur vers la chaudière à haute pression. Dans ce processus, l’environnement travaille sur le fluide, augmentant son enthalpie (h = u + pv) et le compressant (augmentant sa pression). En revanche, l’entropie reste inchangée. Le travail requis pour le compresseur est donné par W Pompes = H 2 – H 1 .
- Apport de chaleur isobare (dans un échangeur de chaleur – chaudière) – Dans cette phase (entre l’état 2 et l’état 3), il y a un transfert de chaleur à pression constante vers le condensat liquide à partir d’une source externe, car la chambre est ouverte pour entrer et sortir. . L’eau d’alimentation (circuit secondaire) est chauffée jusqu’au point d’ébullition (2 → 3a) de ce fluide puis évaporée dans la chaudière (3a → 3). La chaleur nette ajoutée est donnée par Q add = H 3 – H 2
- Expansion isentropique (expansion dans une turbine à vapeur) – La vapeur de la chaudière se détend adiabatiquement de l’état 3 à l’état 4 dans une turbine à vapeur pour produire du travail, puis est évacuée vers le condenseur (partiellement condensée). La vapeur fonctionne sur l’environnement (pales de la turbine) et perd une quantité d’enthalpie égale au travail qui quitte le système. Le travail effectué par turbine est donné par W T = H 4 – H 3 . Encore une fois, l’entropie reste inchangée.
- Rejet de chaleur isobare (dans un échangeur de chaleur) – Dans cette phase, le cycle se termine par un processus à pression constante dans lequel la chaleur est rejetée de la vapeur partiellement condensée. Il y a un transfert de chaleur de la vapeur à l’eau de refroidissement circulant dans un circuit de refroidissement. La vapeur se condense et la température de l’eau de refroidissement augmente. La chaleur nette rejetée est donnée par Q re = H 4 – H 1
Lors d’un cycle de Rankine, des travaux sont effectués sur le fluide par les pompes entre les états 1 et 2 ( i compression sentropique ). Le travail est effectué par le fluide dans la turbine entre les étages 3 et 4 ( i expansion sentropique ). La différence entre le travail effectué par le fluide et le travail effectué sur le fluide est le travail net produit par le cycle et correspond à l’aire délimitée par la courbe du cycle (en diagramme pV). Le fluide de travail dans un cycle de Rankine suit une boucle fermée et est réutilisé en permanence.
Comme on peut le voir, il est commode d’utiliser l’enthalpie et le première principe en termes d’enthalpie dans l’analyse de ce cycle thermodynamique. Cette forme de loi simplifie la description du transfert d’énergie . À pression constante , le changement d’enthalpie est égal à l’ énergie transférée de l’environnement par le chauffage:
Processus isobare (Vdp = 0):
dH = dQ → Q = H 2 – H 1
À entropie constante , c’est-à-dire dans un processus isentropique, le changement d’enthalpie est égal au travail de processus d’écoulement effectué sur ou par le système:
Processus isentropique (dQ = 0):
dH = Vdp → W = H 2 – H 1
Voir aussi: Pourquoi les ingénieurs motoristes utilisent l’enthalpie? Réponse: dH = dQ + Vdp
Processus isentropique
Un processus isentropique est un processus thermodynamique , dans lequel l’ entropie du fluide ou du gaz reste constante. Cela signifie que le processus isentropique est un cas particulier d’un processus adiabatique dans lequel il n’y a pas de transfert de chaleur ou de matière. Il s’agit d’un processus adiabatique réversible . L’hypothèse d’absence de transfert de chaleur est très importante, car nous ne pouvons utiliser l’approximation adiabatique que dans des processus très rapides .
Processus isentropique et première loi
Pour un système fermé, on peut écrire la première loi de la thermodynamique en termes d’enthalpie :
dH = dQ + Vdp
ou
dH = TdS + Vdp
Processus isentropique (dQ = 0):
dH = Vdp → W = H 2 – H 1
Processus isobare
Un processus isobare est un processus thermodynamique , dans lequel la pression du système reste constante (p = const). Le transfert de chaleur dans ou hors du système fonctionne, mais modifie également l’énergie interne du système.
Puisqu’il y a des changements d’ énergie interne (dU) et des changements de volume du système (∆V), les ingénieurs utilisent souvent l’ enthalpie du système, qui est définie comme:
H = U + pV
Processus isobare et première loi
La forme classique de la première loi de la thermodynamique est l’équation suivante:
dU = dQ – dW
Dans cette équation, dW est égal à dW = pdV et est connu comme le travail aux limites . Dans un procédé isobare et le gaz parfait, une partie de la chaleur ajoutée au système sera utilisée pour faire le travail et une partie de la chaleur ajoutée augmentera l’ énergie interne (augmentera la température). Par conséquent, il est commode d’utiliser l’ enthalpie au lieu de l’énergie interne.
Processus isobare (Vdp = 0):
dH = dQ → Q = H 2 – H 1
À entropie constante , c’est-à-dire dans un processus isentropique, le changement d’enthalpie est égal au travail de processus d’écoulement effectué sur ou par le système.
Cycle de Rankine – diagramme pV, Ts
Le cycle de Rankine est souvent tracé sur un diagramme pression-volume (diagramme pV ) et sur un diagramme température-entropie ( diagramme Ts ).
Lorsqu’ils sont tracés sur un diagramme de volume de pression , les processus isobares suivent les lignes isobares pour le gaz (les lignes horizontales), les processus adiabatiques se déplacent entre ces lignes horizontales et la zone délimitée par la piste cyclable complète représente le travail total qui peut être effectué au cours d’une cycle.
Le diagramme température-entropie (diagramme Ts) dans laquelle l’état thermodynamique est défini par un point sur un graphique avec l’ entropie déterminée (s) en tant que l’axe horizontal et la température absolue (T) comme axe vertical. Les diagrammes Ts sont un outil utile et courant, notamment parce qu’il permet de visualiser le transfert de chaleur au cours d’un processus. Pour les processus réversibles (idéaux), l’aire sous la courbe Ts d’un processus est la chaleur transférée au système pendant ce processus.
Efficacité thermique du cycle de Rankine
En général , le rendement thermique , η e , d’un moteur thermique est définie comme étant le rapport entre le travail qu’elle fait, W , à la chaleur d’ entrée à la température élevée, Q H .
L’ efficacité thermique , η th , représente la fraction de chaleur , Q H , qui est convertie en travail . Puisque l’énergie est conservée selon la première loi de la thermodynamique et que l’énergie ne peut pas être convertie pour fonctionner complètement, l’apport de chaleur, Q H , doit être égal au travail effectué, W, plus la chaleur qui doit être dissipée sous forme de chaleur résiduelle Q C dans le environnement. Par conséquent, nous pouvons réécrire la formule de l’efficacité thermique comme suit:
C’est une formule très utile, mais ici nous exprimons l’efficacité thermique en utilisant le première principe en termes d’ enthalpie .
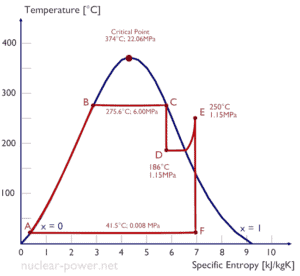
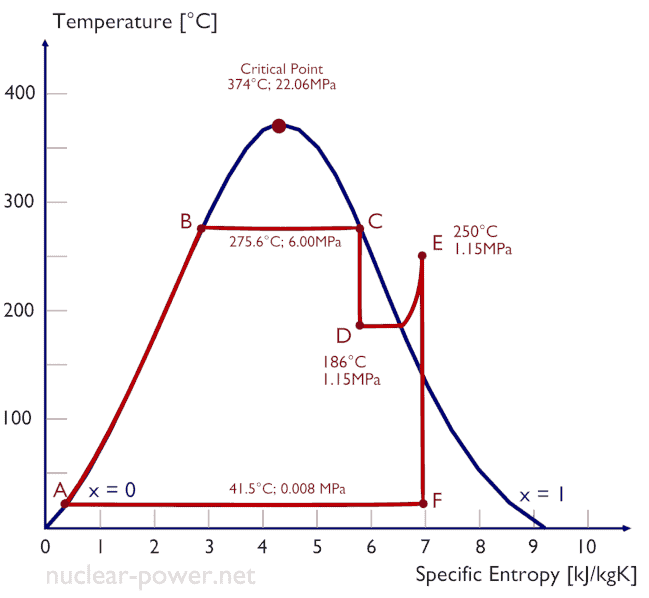
La plupart des centrales nucléaires exploitent généralement des turbines à vapeur à condensation à plusieurs étages . Dans ces turbines, l’étage haute pression reçoit de la vapeur (cette vapeur est presque de la vapeur saturée – x = 0,995 – point C sur la figure; 6 MPa ; 275,6 ° C) d’un générateur de vapeur et l’évacue vers un séparateur-réchauffeur d’humidité (point D ). La vapeur doit être réchauffée afin d’éviter les dommages qui pourraient être causés aux pales de la turbine à vapeur par une vapeur de mauvaise qualité . Le réchauffeur chauffe la vapeur (point D), puis la vapeur est dirigée vers l’étage basse pression de la turbine à vapeur, où elle se détend (point E à F). La vapeur évacuée se condense ensuite dans le condenseur et se trouve à une pression bien inférieure à la pression atmosphérique (pression absolue de0,008 MPa ), et est dans un état partiellement condensé (point F), généralement d’une qualité proche de 90%.
Dans ce cas, les générateurs de vapeur, les turbines à vapeur, les condenseurs et les pompes à eau d’alimentation constituent un moteur thermique, soumis aux limitations d’efficacité imposées par la deuxième loi de la thermodynamique . Dans le cas idéal (pas de frottement, processus réversibles, conception parfaite), ce moteur thermique aurait une efficacité Carnot de
= 1 – T froid / T chaud = 1 – 315/549 = 42,6%
où la température du réservoir chaud est de 275,6 ° C (548,7 K), la température du réservoir froid est de 41,5 ° C (314,7 K). Mais la centrale nucléaire est le véritable moteur thermique , dans lequel les processus thermodynamiques sont en quelque sorte irréversibles. Ils ne se font pas infiniment lentement. Dans les appareils réels (tels que les turbines, les pompes et les compresseurs), un frottement mécanique et des pertes de chaleur entraînent d’autres pertes d’efficacité.
Pour calculer l’ efficacité thermique du cycle de Rankine le plus simple (sans réchauffage), les ingénieurs utilisent la première loi de la thermodynamique en termes d’enthalpie plutôt qu’en termes d’énergie interne.
La première loi en matière d’enthalpie est:
dH = dQ + Vdp
Dans cette équation, le terme Vdp est un travail de processus d’écoulement. Ce travail, Vdp , est utilisé pour des systèmes à flux ouvert comme une turbine ou une pompe dans lesquels il y a un «dp» , c’est-à-dire un changement de pression. Il n’y a aucun changement dans le volume de contrôle . Comme on peut le voir, cette forme de loi simplifie la description du transfert d’énergie . À pression constante , le changement d’enthalpie est égal à l’ énergie transférée de l’environnement par le chauffage:
Processus isobare (Vdp = 0):
dH = dQ → Q = H 2 – H 1
À entropie constante , c’est-à-dire dans un processus isentropique, le changement d’enthalpie est égal au travail de processus d’écoulement effectué sur ou par le système:
Processus isentropique (dQ = 0):
dH = Vdp → W = H 2 – H 1
Il est évident, il sera très utile dans l’analyse des deux cycles thermodynamiques utilisés en génie énergétique, c’est-à-dire dans le cycle de Brayton et le cycle de Rankine.
L’ enthalpie peut être transformée en une variable intensive ou spécifique , en la divisant par la masse . Les ingénieurs utilisent l’ enthalpie spécifique dans l’analyse thermodynamique plus que l’enthalpie elle-même. Il est tabulé dans les tableaux de vapeur avec un volume spécifique et une énergie interne spécifique . L’efficacité thermique d’un tel cycle de Rankine simple et en termes d’enthalpies spécifiques serait:
C’est une équation très simple et pour déterminer l’efficacité thermique, vous pouvez utiliser les données des tables de vapeur .
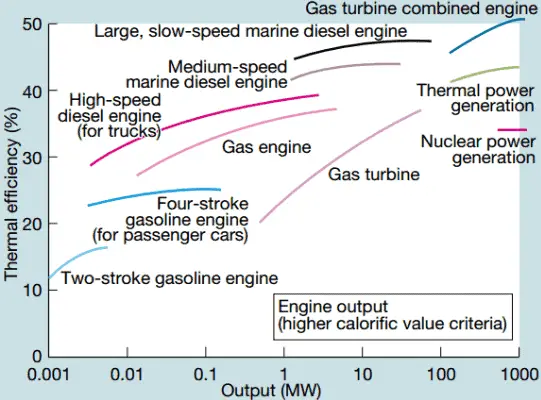
Dans les centrales nucléaires modernes, le rendement thermique global est d’environ un tiers (33%), de sorte que 3000 MWth d’énergie thermique provenant de la réaction de fission sont nécessaires pour générer 1000 MWe d’énergie électrique. La raison en est la température de vapeur relativement basse ( 6 MPa ; 275,6 ° C). Des rendements plus élevés peuvent être atteints en augmentant la températurede la vapeur. Mais cela nécessite une augmentation des pressions à l’intérieur des chaudières ou des générateurs de vapeur. Cependant, des considérations métallurgiques imposent des limites supérieures à ces pressions. Par rapport à d’autres sources d’énergie, le rendement thermique de 33% n’est pas beaucoup. Mais il faut noter que les centrales nucléaires sont beaucoup plus complexes que les centrales à combustibles fossiles et qu’il est beaucoup plus facile de brûler des combustibles fossiles que de produire de l’énergie à partir de combustibles nucléaires. Les centrales électriques à combustibles fossiles sous-critiques, qui fonctionnent sous une pression critique (c’est-à-dire inférieure à 22,1 MPa), peuvent atteindre une efficacité de 36 à 40%.
Causes d’inefficacité
Comme cela a été discuté, une efficacité peut varier entre 0 et 1. Chaque moteur thermique est en quelque sorte inefficace. Cette inefficacité peut être attribuée à trois causes.
- Irréversibilité des processus . Il existe une limite supérieure théorique globale à l’efficacité de la conversion de la chaleur pour fonctionner dans n’importe quel moteur thermique. Cette limite supérieure est appelée efficacité Carnot . Selon le principe Carnot , aucun moteur ne peut être plus efficace qu’un moteur réversible ( un moteur thermique Carnot ) fonctionnant entre les mêmes réservoirs haute température et basse température. Par exemple, lorsque le réservoir chaud a T chaud de 400 ° C (673 K) et T froid d’environ 20 ° C (293 K), l’efficacité maximale (idéale) sera: = 1 – T froid / T chaud = 1 – 293 / 673 = 56%. Mais tous les processus thermodynamiques réels sont en quelque sorte irréversibles. Ils ne se font pas infiniment lentement. Par conséquent, les moteurs thermiques doivent avoir des rendements inférieurs aux limites de leur rendement en raison de l’irréversibilité inhérente du cycle du moteur thermique qu’ils utilisent.
- Présence de friction et de pertes de chaleur. Dans les systèmes thermodynamiques réels ou dans les moteurs thermiques réels, une partie de l’inefficacité globale du cycle est due aux pertes des composants individuels. Dans les appareils réels (tels que les turbines, les pompes et les compresseurs), un frottement mécanique , des pertes de chaleur et des pertes dans le processus de combustion entraînent des pertes d’efficacité supplémentaires.
- Inefficacité de la conception . Enfin, la dernière et aussi importante source d’inefficacité provient des compromis faits par les ingénieurs lors de la conception d’un moteur thermique (par exemple une centrale électrique). Ils doivent tenir compte des coûts et d’autres facteurs dans la conception et le fonctionnement du cycle. À titre d’exemple, considérons la conception du condenseur dans les centrales thermiques. Idéalement, la vapeur évacuée dans le condenseur n’aurait pas de sous-refroidissement . Mais les vrais condenseurs sont conçus pour sous-refroidir le liquide de quelques degrés Celsius afin d’éviter la cavitation d’aspiration dans les pompes à condensats. Mais, ce sous-refroidissement augmente l’inefficacité du cycle, car plus d’énergie est nécessaire pour réchauffer l’eau.
Amélioration de l’efficacité thermique – Cycle de Rankine
Il existe plusieurs méthodes, comment améliorer l’efficacité thermique du cycle de Rankine. En supposant que la température maximale est limitée par la pression à l’intérieur de l’enceinte sous pression du réacteur, ces méthodes sont les suivantes:
- Pressions des chaudières et des condenseurs
- Surchauffe et réchauffage
- Régénération de chaleur
- Cycle de Rankine supercritique
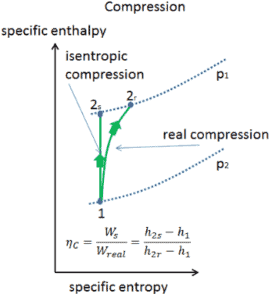
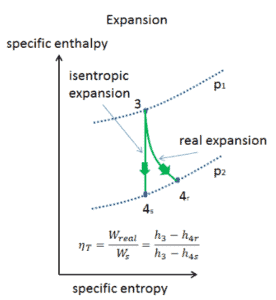
Efficacité isentropique – Turbine, pompe
Dans les chapitres précédents, nous avons supposé que l’expansion de la vapeur est isentropique et nous avons donc utilisé T 4, soit la température de sortie du gaz. Ces hypothèses ne sont applicables qu’avec des cycles idéaux.
La plupart des appareils à débit constant (turbines, compresseurs, buses) fonctionnent dans des conditions adiabatiques, mais ils ne sont pas vraiment isentropiques mais sont plutôt idéalisés comme isentropiques à des fins de calcul. Nous définissons les paramètres η T , η P , η N , comme un rapport entre le travail réel effectué par appareil et le travail par appareil lorsqu’il est utilisé dans des conditions isentropiques (dans le cas d’une turbine). Ce rapport est connu sous le nom d’ efficacité turbine isentropique / pompe / buse . Ces paramètres décrivent l’efficacité avec laquelle une turbine, un compresseur ou une buse se rapproche d’un dispositif isentropique correspondant. Ce paramètre réduit l’efficacité globale et le rendement de travail. Pour les turbines, la valeur de η T est généralement de 0,7 à 0,9 (70–90%).
Voir aussi: Processus isentropique
Cycle de Rankine – Problème avec la solution
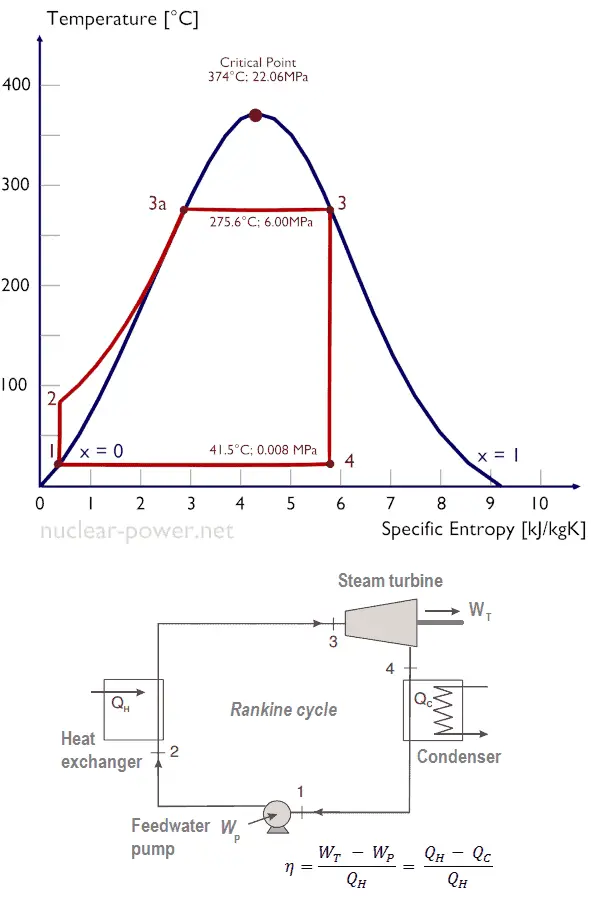 Supposons le cycle de Rankine , qui est l’un des cycles thermodynamiques les plus courants dans les centrales thermiques. Dans ce cas, supposons un cycle simple sans réchauffage et sans avec turbine à vapeur à condensation fonctionnant à la vapeur saturée (vapeur sèche). Dans ce cas, la turbine fonctionne à l’état stable avec des conditions d’entrée de 6 MPa, t = 275,6 ° C, x = 1 (point 3). La vapeur sort de cet étage de turbine à une pression de 0,008 MPa, 41,5 ° C et x = ??? (point 4).
Supposons le cycle de Rankine , qui est l’un des cycles thermodynamiques les plus courants dans les centrales thermiques. Dans ce cas, supposons un cycle simple sans réchauffage et sans avec turbine à vapeur à condensation fonctionnant à la vapeur saturée (vapeur sèche). Dans ce cas, la turbine fonctionne à l’état stable avec des conditions d’entrée de 6 MPa, t = 275,6 ° C, x = 1 (point 3). La vapeur sort de cet étage de turbine à une pression de 0,008 MPa, 41,5 ° C et x = ??? (point 4).
Calculer:
- la qualité de la vapeur de la vapeur de sortie
- la différence d’enthalpie entre ces deux états (3 → 4), ce qui correspond au travail effectué par la vapeur, W T .
- la différence d’enthalpie entre ces deux états (1 → 2), qui correspond au travail effectué par les pompes, W P .
- la différence d’enthalpie entre ces deux états (2 → 3), qui correspond à la chaleur nette ajoutée dans le générateur de vapeur
- l’efficacité thermodynamique de ce cycle et comparer cette valeur avec l’efficacité de Carnot
1)
Comme nous ne connaissons pas la qualité exacte de la vapeur de la vapeur de sortie, nous devons déterminer ce paramètre. L’état 4 est fixé par la pression p 4 = 0,008 MPa et le fait que l’ entropie spécifique est constante pour l’expansion isentropique (s 3 = s 4 = 5,89 kJ / kgK pour 6 MPa ). L’entropie spécifique de l’eau liquide saturée (x = 0) et de la vapeur sèche (x = 1) peut être choisie dans les tables de vapeur . En cas de vapeur humide, l’entropie réelle peut être calculée avec la qualité de la vapeur, x, et les entropies spécifiques de l’eau liquide saturée et de la vapeur sèche:
s 4 = s v x + (1 – x) s l
où
s 4 = entropie de vapeur humide (J / kg K) = 5,89 kJ / kgK
s v = entropie de vapeur «sèche» (J / kg K) = 8,227 kJ / kgK (pour 0,008 MPa)
s l = entropie d’eau liquide saturée (J / kg K) = 0,592 kJ / kgK (pour 0,008 MPa)
D’après cette équation, la qualité de la vapeur est:
x 4 = ( s 4 – s l ) / ( s v – s l ) = (5,89 – 0,592) / (8,227 – 0,592) = 0,694 = 69,4%
2)
L’enthalpie pour l’état 3 peut être prélevée directement dans les tables de vapeur, tandis que l’enthalpie pour l’état 4 doit être calculée en utilisant la qualité de la vapeur:
h 3, v = 2785 kJ / kg
h 4, humide = h 4, v x + (1 – x) h 4, l = 2576. 0,694 + (1 – 0,694). 174 = 1787 + 53,2 = 1840 kJ / kg
Ensuite, le travail effectué par la vapeur, W T, est
W T = Δh = 945 kJ / kg
3)
L’enthalpie pour l’état 1 peut être sélectionnée directement dans les tables à vapeur:
h 1, l = 174 kJ / kg
L’état 2 est fixé par la pression p 2 = 6,0 MPa et le fait que l’entropie spécifique est constante pour la compression isentropique (s 1 = s 2 = 0,592 kJ / kgK pour 0,008 MPa ). Pour cette entropie s 2 = 0,592 kJ / kgK et p 2 = 6,0 MPa, nous trouvons h 2, sous-refroidi dans les tables de vapeur pour l’eau comprimé (en utilisant l’interpolation entre deux états).
h 2, sous-refroidi = 179,7 kJ / kg
Ensuite, le travail effectué par les pompes, W P, est
W P = Δh = 5,7 kJ / kg
4)
La différence d’enthalpie entre (2 → 3), qui correspond à la chaleur nette ajoutée dans le générateur de vapeur, est simplement:
Q add = h 3, v – h 2, sous-refroidi = 2785 – 179,7 = 2605,3 kJ / kg
Notez qu’il n’y a pas de régénération de chaleur dans ce cycle. En revanche, la plus grande partie de la chaleur ajoutée est destinée à l’enthalpie de vaporisation (c’est-à-dire au changement de phase).
5)
Dans ce cas, les générateurs de vapeur, les turbines à vapeur, les condenseurs et les pompes à eau d’alimentation constituent un moteur thermique, soumis aux limitations d’efficacité imposées par la deuxième loi de la thermodynamique . Dans le cas idéal (pas de frottement, processus réversibles, conception parfaite), ce moteur thermique aurait une efficacité Carnot de
η Carnot = 1 – T froid / T chaud = 1 – 315/549 = 42,6%
où la température du réservoir chaud est de 275,6 ° C (548,7 K), la température du réservoir froid est de 41,5 ° C (314,7 K).
L’efficacité thermodynamique de ce cycle peut être calculée par la formule suivante:
donc
η th = (945 – 5,7) / 2605,3 = 0,361 = 36,1%
Cet article est basé sur la traduction automatique de l’article original en anglais. Pour plus d’informations, voir l’article en anglais. Pouvez vous nous aider Si vous souhaitez corriger la traduction, envoyez-la à l’adresse: translations@nuclear-power.com ou remplissez le formulaire de traduction en ligne. Nous apprécions votre aide, nous mettrons à jour la traduction le plus rapidement possible. Merci