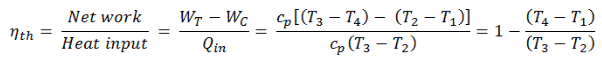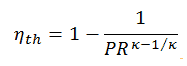Eficiência térmica do ciclo de Brayton
Em geral, a eficiência térmica , η th , de qualquer motor de calor é definida como a razão entre o trabalho que faz, W , para o calor de entrada a uma temperatura elevada, Q H .
A eficiência térmica , η th , representa a fração de calor , Q H , que é convertida em trabalho . Como a energia é conservada de acordo com a primeira lei da termodinâmica e a energia não pode ser convertida para funcionar completamente, a entrada de calor, Q H , deve ser igual ao trabalho realizado, W, mais o calor que deve ser dissipado como calor residual Q C no meio Ambiente. Portanto, podemos reescrever a fórmula da eficiência térmica como:
Essa é uma fórmula muito útil, mas aqui expressamos a eficiência térmica usando a primeira lei em termos de entalpia .
Para calcular a eficiência térmica do ciclo de Brayton (compressor único e turbina única), os engenheiros usam a primeira lei da termodinâmica em termos de entalpia e não em energia interna.
A primeira lei em termos de entalpia é:
dH = dQ + Vdp
Nesta equação, o termo Vdp é um trabalho de processo de fluxo. Este trabalho, Vdp , é usado para sistemas de fluxo aberto como uma turbina ou uma bomba na qual existe um “dp” , ou seja, mudança de pressão. Não há alterações no volume de controle . Como pode ser visto, essa forma de lei simplifica a descrição da transferência de energia .
Existem expressões em termos de variáveis mais familiares, como temperatura e pressão :
dH = C p dT + V (1-aT) dp
Onde C p é a capacidade calorífica a pressão constante e α é o coeficiente de expansão térmica (cúbico). Para o gás ideal αT = 1 e, portanto:
dH = C p dT
A pressão constante , a mudança de entalpia é igual à energia transferida do ambiente através do aquecimento:
Processo isobárico (Vdp = 0):
dH = dQ → Q = H 3 – H 2 → H 3 – H 2 = C P (T 3 – T 2 )
Na entropia constante , ou seja, no processo isentrópico, a mudança de entalpia é igual ao trabalho do processo de fluxo realizado no ou pelo sistema:
Processo isentrópico (dQ = 0):
dH = Vdp → W = H 4 – H 3 → H 4 – H 3 = C p (T 4 – T 3 )
A entalpia pode ser transformada em uma variável intensiva ou específica dividindo-se pela massa . Os engenheiros usam mais a entalpia específica na análise termodinâmica do que a própria entalpia.
Agora, vamos assumir o ciclo de Brayton ideal que descreve o funcionamento de um motor de calor com pressão constante. Os modernos motores de turbina a gás e os motores a jato de respiração também seguem o ciclo de Brayton. Esse ciclo consiste em quatro processos termodinâmicos:
-
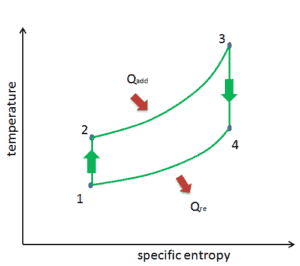
Ciclo de Brayton – diagrama de Ts compressão isentrópica – o ar ambiente é aspirado para o compressor, onde é pressurizado (1 → 2). O trabalho necessário para o compressor é dado por W C = H 2 – H 1 .
- adição de calor isobárico – o ar comprimido passa por uma câmara de combustão, onde o combustível é queimado e o ar ou outro meio é aquecido (2 → 3). É um processo de pressão constante, já que a câmara está aberta para entrar e sair. O calor líquido adicionado é dado por Q add = H 3 – H 2
- expansão isentrópica – o ar aquecido e pressurizado se expande na turbina, gasta sua energia. O trabalho realizado pela turbina é dado por W T = H 4 – H 3
- rejeição de calor isobárica – o calor residual deve ser rejeitado para fechar o ciclo. O calor líquido rejeitado é dado por Q re = H 4 – H 1
Como pode ser visto, podemos descrever e calcular completamente esses ciclos (da mesma forma para o ciclo de Rankine) usando entalpias.
Eficiência térmica – Ciclo de Brayton
A eficiência térmica desse ciclo simples de Brayton, para o gás ideal, agora pode ser expressa em termos de temperatura:
Onde
- W t o trabalho realizado pelo gás na turbina
- W C o trabalho realizado no gás no compressor
- c p é a razão de capacidade térmica
Relação de Pressão – Ciclo de Brayton – Turbina a Gás
A eficiência térmica em termos da razão de pressão do compressor (PR = p 2 / p 1 ), que é o parâmetro comumente usado:
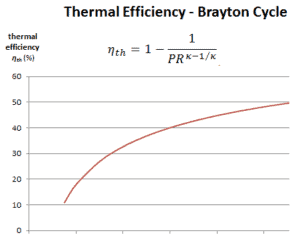Em geral, aumentar a taxa de pressão é a maneira mais direta de aumentar a eficiência térmica geral de um ciclo de Brayton, porque o ciclo se aproxima do ciclo de Carnot.
De acordo com o princípio de Carnot, é possível obter maiores eficiências aumentando a temperatura do gás.
Mas também há limites nas relações de pressão que podem ser usadas no ciclo. A temperatura mais alta do ciclo ocorre no final do processo de combustão e é limitada pela temperatura máxima que as pás da turbina podem suportar. Como de costume, considerações metalúrgicas (cerca de 1700 K) impõem limites superiores à eficiência térmica.
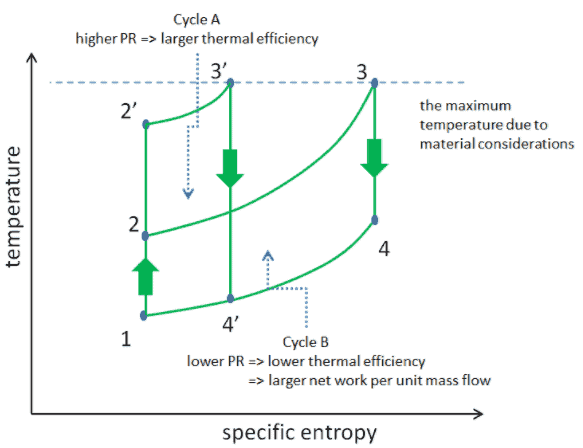
Considere o efeito da taxa de pressão do compressor na eficiência térmica quando a temperatura de entrada da turbina estiver restrita à temperatura máxima permitida. Existem dois diagramas Ts dos ciclos de Brayton com a mesma temperatura de entrada da turbina, mas diferentes proporções de pressão do compressor na imagem. Como pode ser visto para uma temperatura de entrada de turbina fixa, a produção líquida de trabalho por ciclo (W net = W T – W C ) diminui com a razão de pressão ( Ciclo A ). Mas o ciclo A tem a maior eficiência.
Por outro lado, o Ciclo B tem uma maior produção líquida de trabalho por ciclo (área delimitada no diagrama) e, portanto, o maior trabalho líquido desenvolvido por unidade de fluxo de massa. O trabalho produzido pelo ciclo vezes uma taxa de fluxo de massa através do ciclo é igual à potência produzida pela turbina a gás.
Portanto, com menos produção de trabalho por ciclo (Ciclo A), é necessária uma taxa de fluxo de massa maior (portanto, um sistema maior ) para manter a mesma produção de energia, o que pode não ser econômico. Essa é a principal consideração no projeto de turbinas a gás, pois aqui os engenheiros devem equilibrar a eficiência térmica e a compactação. Nos projetos mais comuns, a razão de pressão de uma turbina a gás varia de cerca de 11 a 16.
Melhoria da eficiência térmica – Brayton Cycle
Existem vários métodos, como pode ser melhorada a eficiência térmica do ciclo de Brayton. Assumindo que a temperatura máxima seja limitada por considerações metalúrgicas, esses métodos são:
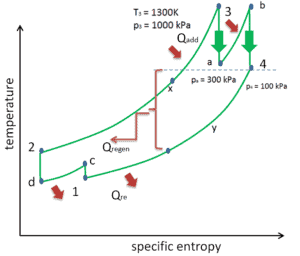
Reaquecimento, Intercooling e Regeneração no Ciclo de Brayton
Como foi discutido, o reaquecimento e o inter-resfriamento são complementares à regeneração de calor . Por si só, eles não necessariamente aumentariam a eficiência térmica; no entanto, quando o inter-resfriamento ou o reaquecimento são usados em conjunto com a regeneração de calor, um aumento significativo na eficiência térmica pode ser alcançado e a produção líquida de trabalho também é aumentada. Isso requer uma turbina a gás com dois estágios de compressão e dois estágios de turbina.
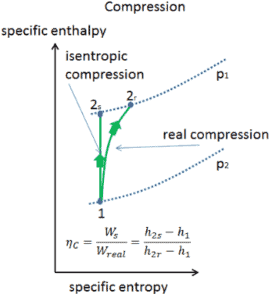
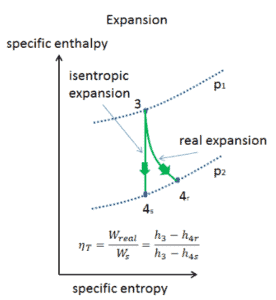
Eficiência isentrópica – turbina, compressor
A maioria dos dispositivos de fluxo constante (turbinas, compressores, bicos) opera em condições adiabáticas , mas não são verdadeiramente isentrópicos, mas são idealizados como isentrópicos para fins de cálculo. Definimos os parâmetros η T , η C , η N , como uma razão entre o trabalho real realizado pelo dispositivo e o trabalho por dispositivo quando operado em condições isentrópicas (no caso de turbinas). Essa relação é conhecida como eficiência isentrópica de turbina / compressor / bico .
Veja também: Irreversibilidade de processos naturais
Esses parâmetros descrevem com que eficiência uma turbina, compressor ou bico se aproxima de um dispositivo isentrópico correspondente. Este parâmetro reduz a eficiência geral e a produção do trabalho. Para turbinas, o valor de η T é tipicamente de 0,7 a 0,9 (70-90%).
……………………………………………………………………………………………………………………………….
Este artigo é baseado na tradução automática do artigo original em inglês. Para mais informações, consulte o artigo em inglês. Você pode nos ajudar. Se você deseja corrigir a tradução, envie-a para: translations@nuclear-power.com ou preencha o formulário de tradução on-line. Agradecemos sua ajuda, atualizaremos a tradução o mais rápido possível. Obrigado.
