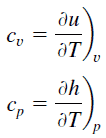O que é a Primeira Lei da Termodinâmica – Definição

Forma da equação:

IntE _int = Q – W

onde E _int representa a energia interna do material, que depende apenas do estado do material (temperatura, pressão e volume). Q é o calor líquido adicionado ao sistema e W é o trabalho líquido realizado pelo sistema. Devemos ser cuidadosos e consistentes ao seguir as convenções de sinal para Q e W. Como W na equação é o trabalho realizado pelo sistema, se o trabalho for realizado no sistema, W será negativo e E _int aumentará.

Da mesma forma, Q é positivo para o calor adicionado ao sistema; portanto, se o calor sai do sistema, Q é negativo. Isso nos diz o seguinte: A energia interna de um sistema tende a aumentar se o calor for absorvido pelo sistema ou se um trabalho positivo for feito no sistema. Por outro lado, a energia interna tende a diminuir se o calor for perdido pelo sistema ou se for feito um trabalho negativo no sistema. Deve-se adicionar Q e W dependem do caminho, enquanto E _int é independente do caminho.

Forma diferencial:

dE _int = dQ – dW

A energia interna E _int de um sistema tende a aumentar se a energia é adicionada como calor Q e tende a diminuir se a energia é perdida como o trabalho W realizado pelo sistema.

Primeira lei em termos de entalpia dH = dQ + Vdp

A entalpia é definida como sendo a soma da energia interna E mais o produto da pressão P e volume V . Em muitas análises termodinâmicas, a soma da energia interna U e o produto da pressão pe volume V aparece; portanto, é conveniente atribuir à combinação um nome, entalpia e um símbolo distinto, H.

H = U + pV

Veja também: Entalpia

A primeira lei da termodinâmica em termos de entalpia mostra-nos por que os engenheiros usam a entalpia em ciclos termodinâmicos (por exemplo, ciclo de Brayton ou ciclo de Rankine ).

A forma clássica da lei é a seguinte equação:

dU = dQ – dW

Nesta equação, dW é igual a dW = pdV e é conhecido como trabalho de fronteira .

dH = dQ + Vdp

ou

dH = TdS + Vdp

Nesta equação, o termo Vdp é um trabalho de processo de fluxo. Este trabalho,   Vdp , é usado para sistemas de fluxo aberto, como uma turbina ou uma bomba na qual existe um “dp” , ou seja, mudança de pressão. Não há alterações no volume de controle . Como pode ser visto, essa forma de lei simplifica a descrição da transferência de energia . A pressão constante , a mudança de entalpia é igual à energia transferida do ambiente através do aquecimento:

Processo isobárico (Vdp = 0):

dH = dQ      →      Q = H ₂ – H ₁

Na entropia constante , ou seja, no processo isentrópico, a mudança de entalpia é igual ao trabalho do processo de fluxo realizado no ou pelo sistema:

Processo isentrópico (dQ = 0):

dH = Vdp      →      W = H ₂ – H ₁

É óbvio que será muito útil na análise de ambos os ciclos termodinâmicos usados ​​na engenharia de energia, ou seja, no ciclo de Brayton e no ciclo de Rankine.

Exemplo: Primeira Lei da Termodinâmica e Ciclo de Brayton

Vamos assumir o ciclo de Brayton ideal que descreve o funcionamento de um motor de calor com pressão constante . Os modernos motores de turbina a gás e os motores a jato de respiração também seguem o ciclo de Brayton. Esse ciclo consiste em quatro processos termodinâmicos:

1. 

   compressão isentrópica – o ar ambiente é aspirado para o compressor, onde é pressurizado (1 → 2). O trabalho necessário para o compressor é dado por W _C = H ₂ – H ₁ .

2. adição de calor isobárico – o ar comprimido passa por uma câmara de combustão, onde o combustível é queimado e o ar ou outro meio é aquecido (2 → 3). É um processo de pressão constante, já que a câmara está aberta para entrar e sair. O calor líquido adicionado é dado por Q _add = H ₃ – H ₂
3. expansão isentrópica – o ar aquecido e pressurizado se expande na turbina, gasta sua energia. O trabalho realizado pela turbina é dado por W _T = H ₄ – H ₃
4. rejeição de calor isobárica – o calor residual deve ser rejeitado para fechar o ciclo. O calor líquido rejeitado é dado por Q _re = H ₄ – H ₁

Como pode ser visto, podemos descrever e calcular (por exemplo, eficiência termodinâmica) esses ciclos (da mesma forma para o ciclo de Rankine ) usando entalpias .

Energia interna

Na termodinâmica, energia interna (também chamada de energia térmica ) é definida como a energia associada a formas microscópicas de energia . É uma quantidade extensa , depende do tamanho do sistema ou da quantidade de substância que ele contém. A unidade SI de energia interna é o joule (J) . É a energia contida no sistema, excluindo a energia cinética do movimento do sistema como um todo e a energia potencial do sistema. As formas microscópicas de energia incluem aquelas devidas à rotação , vibração, translação e interaçõesentre as moléculas de uma substância. Nenhuma dessas formas de energia pode ser medida ou avaliada diretamente, mas foram desenvolvidas técnicas para avaliar a mudança na soma total de todas essas formas microscópicas de energia.

Além disso, a energia é armazenada nas ligações químicas entre os átomos que compõem as moléculas. Esse armazenamento de energia no nível atômico inclui energia associada a estados orbitais de elétrons, rotação nuclear e forças de ligação no núcleo.

Energia microscópica

A energia interna envolve energia na escala microscópica . Pode ser dividido em energia microscópica potencial, _pote U e energia cinética microscópica, U _kin , componentes:

U = U _pote + U _parentes

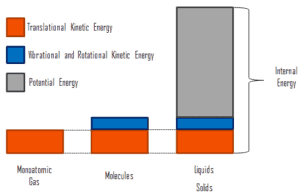onde a energia cinética microscópica, U _kin , envolve os movimentos de todas as partículas do sistema em relação à estrutura do centro de massa. Para um gás monatômico ideal , essa é apenas a energia cinética translacional do movimento linear dos átomos. Partículas monoatômicas não giram ou vibram. O comportamento do sistema é bem descrito pela teoria cinética dos gases. A teoria cinética baseia-se no fato de que durante uma colisão elástica entre uma molécula com alta energia cinética e outra com baixa energia cinética, parte da energia será transferida para a molécula de energia cinética inferior. No entanto, para gases poliatômicos, existem rotações eenergia cinética vibracional também.

A energia potencial microscópica, U _pot , envolve as ligações químicas entre os átomos que compõem as moléculas, as forças de ligação no núcleo e também os campos de força física no sistema (por exemplo, campos elétricos ou magnéticos).

Em líquidos e sólidos, há um componente significativo da energia potencial associada às forças de atração intermoleculares .

Calor e Trabalho

Vimos que a energia interna muda com Q , que é o calor líquido adicionado ao sistema e W , que é o trabalho líquido realizado pelo sistema. Agora examinamos como o trabalho realizado e o calor adicionado ao sistema durante um processo termodinâmico dependem dos detalhes de como o processo ocorre.

Calor na Termodinâmica

Enquanto energia interna se refere à energia total de todas as moléculas dentro do objeto, o calor é a quantidade de energia que flui de um corpo para outro espontaneamente devido à diferença de temperatura. O calor é uma forma de energia, mas é energia em trânsito . O calor não é propriedade de um sistema. No entanto, a transferência de energia como calor ocorre no nível molecular como resultado de uma diferença de temperatura .

Considere um bloco de metal em alta temperatura, que consiste em átomos que oscilam intensamente em torno de suas posições médias. A baixas temperaturas , os átomos continuam a oscilar, mas com menos intensidade . Se um bloco mais quente de metal é colocado em contato com um bloco mais frio, os átomos intensamente oscilantes na borda do bloco mais quente emitem sua energia cinética para os átomos menos oscilantes na borda do bloco frio. Nesse caso, há transferência de energia entre esses dois blocos e o calor flui do bloco mais quente para o mais frio por essas vibrações aleatórias.

Em geral, quando dois objetos são colocados em contato térmico , o calor flui entre eles até que entrem em equilíbrio um com o outro. Quando existe uma diferença de temperatura , o calor flui espontaneamente do sistema mais quente para o sistema mais frio . A transferência de calor ocorre por condução ou por radiação térmica . Quando o fluxo de calor para , diz-se que está na mesma temperatura . Dizem que eles estão em equilíbrio térmico .

Como no trabalho, a quantidade de calor transferida depende do caminho e não simplesmente das condições iniciais e finais do sistema. Na verdade, existem muitas maneiras de levar o gás do estado i para o estado f.

Além disso, como no trabalho, é importante distinguir entre o calor adicionado a um sistema do ambiente e o calor removido do sistema para o ambiente. Q é positivo para o calor adicionado ao sistema, portanto, se o calor sai do sistema, Q é negativo. Como W na equação é o trabalho realizado pelo sistema, se o trabalho for realizado no sistema, W será negativo e E _int aumentará.

O símbolo q é usado algumas vezes para indicar o calor adicionado ou removido de um sistema por unidade de massa . É igual ao calor total (Q) adicionado ou removido dividido pela massa (m).

Capacidade de calor

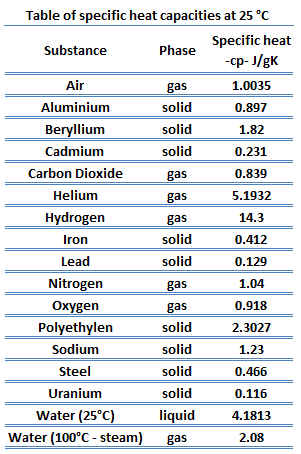Diferentes substâncias são afetadas em diferentes magnitudes pela adição de calor . Quando uma determinada quantidade de calor é adicionada a diferentes substâncias, suas temperaturas aumentam em diferentes quantidades. Essa constante de proporcionalidade entre o calor Q que o objeto absorve ou perde e a mudança de temperatura resultante T do objeto é conhecida como capacidade de calor C de um objeto.

C = Q / ΔT

A capacidade de calor é uma propriedade extensiva da matéria, o que significa que é proporcional ao tamanho do sistema. A capacidade térmica C tem a unidade de energia por grau ou energia por kelvin. Ao expressar o mesmo fenômeno que uma propriedade intensiva , a capacidade de calor é dividida pela quantidade de substância, massa ou volume, portanto, a quantidade é independente do tamanho ou extensão da amostra.

Capacidade específica de calor

A capacidade térmica de uma substância por unidade de massa é denominada capacidade térmica específica (c _p ) da substância. O índice p indica que a capacidade térmica e a capacidade térmica específica se aplicam quando o calor é adicionado ou removido a pressão constante .

c _p = Q / mΔT

Capacidade de calor específica do gás ideal

No Modelo de Gás Ideal , as propriedades intensivas c _v e c _p são definidas para substâncias compressíveis puras e simples como derivadas parciais da energia interna u (T, v) e entalpia h (T, p) , respectivamente:

onde os subscritos v e p denotam as variáveis ​​mantidas fixas durante a diferenciação. As propriedades c _v e c _p são referidos como calores específicos (ou capacidades de calor ), porque, sob determinadas condições especiais dizem respeito a mudança de temperatura de um sistema para a quantidade de energia adicionada pela transferência de calor. As suas unidades SI são J / kg K ou J / mol K . Dois aquecimentos específicos são definidos para gases, um para volume constante (c _v ) e outro para pressão constante (c _p ) .

De acordo com a primeira lei da termodinâmica , para processos de volume constante com um gás ideal monatômico, o calor molar específico será:

C _v = 3 / 2R = 12,5 J / mol K

Porque

U = 3 / 2nRT

Pode-se derivar que o calor molar específico a pressão constante é:

C _p = C _v + R = 5 / 2R = 20,8 J / mol K

Este C _p é maior do que o calor específico molar a volume constante C _v , porque a energia deve agora ser fornecidos não só para aumentar a temperatura do gás, mas também para o gás de trabalho para fazer porque neste volume caso alterações.

Calor latente de vaporização

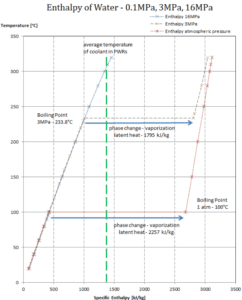
Em geral, quando um material muda de fase de sólido para líquido ou de líquido para gás, uma certa quantidade de energia está envolvida nessa mudança de fase. No caso de mudança de fase de líquido para gás, essa quantidade de energia é conhecida como entalpia de vaporização (símbolo ∆H _vap ; unidade: J), também conhecida como calor (latente) de vaporização ou calor de evaporação. Calor latente é a quantidade de calor adicionada ou removida de uma substância para produzir uma mudança de fase. Essa energia decompõe as forças atraentes intermoleculares e também deve fornecer a energia necessária para expandir o gás (o trabalho pΔV) Quando o calor latente é adicionado, nenhuma mudança de temperatura ocorre. A entalpia da vaporização é uma função da pressão na qual essa transformação ocorre.

Calor latente de vaporização – água a 0,1 MPa (pressão atmosférica)

h _lg = 2257 kJ / kg

Calor latente de vaporização – água a 3 MPa (pressão dentro de um gerador de vapor)

h _lg = 1795 kJ / kg

Calor latente de vaporização – água a 16 MPa (pressão dentro de um pressurizador )

h _lg = 931 kJ / kg

O calor da vaporização diminui com o aumento da pressão, enquanto o ponto de ebulição aumenta. Ele desaparece completamente em um determinado ponto chamado ponto crítico . Acima do ponto crítico, as fases líquida e de vapor são indistinguíveis, e a substância é chamada de fluido supercrítico .

O calor da vaporização é o calor necessário para vaporizar completamente uma unidade de líquido saturado (ou condensar uma unidade de massa de vapor saturado) e é igual a h _lg = h _g – h _l .

O calor necessário para derreter (ou congelar) uma unidade de massa na substância a pressão constante é o calor da fusão e é igual a h _sl = h _l – h _s , onde h _s é a entalpia do sólido saturado e h _l é a entalpia do líquido saturado.

Trabalho em Termodinâmica

Na termodinâmica, o trabalho realizado por um sistema é a energia transferida pelo sistema para os arredores. Energia cinética, energia potencial e energia interna são formas de energia que são propriedades de um sistema. O trabalho é uma forma de energia , mas é energia em trânsito . Um sistema não contém trabalho, trabalho é um processo realizado por ou em um sistema. Em geral, o trabalho é definido para sistemas mecânicos como a ação de uma força sobre um objeto a distância.

W = F. d

Onde:

W = trabalho (J)

F = força (N)

d = deslocamento (m)

Trabalho pΔV

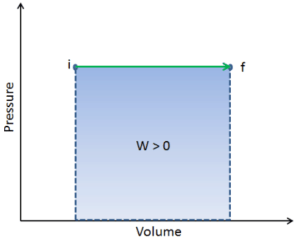
O trabalho de volume de pressão (ou pΔV Work ) ocorre quando o volume V de um sistema é alterado. O trabalho pΔV é igual à área sob a curva do processo plotada no diagrama pressão-volume. É conhecido também como o trabalho de fronteira . O trabalho de limite  ocorre porque a massa da substância contida no limite do sistema faz com que uma força, a pressão vezes a área da superfície, atue na superfície do limite e faça com que ela se mova. O trabalho de limite  (ou  pΔV Work ) ocorre quando o  volume V de um sistema é alterado . É usado para calcular o trabalho de deslocamento do pistão em um  sistema fechado    . É o que acontece quando o  vapor ou gás contido em um dispositivo de cilindro e pistão se expande contra o pistão e força o pistão a se mover.

Exemplo:

Considere-se um pistão de atrito que é usado para proporcionar uma pressão constante de 500 kPa num cilindro contendo vapor ( vapor sobreaquecido ) de um volume de 2 m ³  a 500 K .

Calcule a temperatura final, se 3000 kJ de calor forem adicionados.

Solução:

Usando tabelas de vapor , sabemos que a entalpia específica desse vapor (500 kPa; 500 K) é de cerca de 2912 kJ / kg . Como nessa condição o vapor possui densidade de 2,2 kg / m ³ , sabemos que há cerca de 4,4 kg de vapor no pistão na entalpia de 2912 kJ / kg x 4,4 kg = 12812 kJ .

Quando usamos simplesmente Q = H ₂ – H ₁ , a entalpia resultante do vapor será:

H ₂ = H ₁ + Q = 15812 kJ

Nas tabelas de vapor , esse vapor superaquecido (15812 / 4,4 = 3593 kJ / kg) terá uma temperatura de 828 K (555 ° C) . Uma vez que nesta entalpia do vapor tem a densidade de 1,31 kg / m ³ , é óbvio que se expandiu em cerca de 2,2 / 1,31 = 1,67 (+ 67%). Portanto, o volume resultante é de 2 m ³ x 1,67 = 3,34 m ³ e ∆V = 3,34 m ³ – 2 m ³ = 1,34 m ³ .

A parte p∆V da entalpia, ou seja, o trabalho realizado é:

W = p∆V = 500 000 Pa x 1,34 m ³ = 670 kJ

———–

Durante a mudança de volume , a pressão e a temperatura também podem mudar. Para calcular esses processos, precisaríamos saber como a pressão varia com o volume do processo real pelo qual o sistema muda do estado i para o estado f . A primeira lei da termodinâmica e o trabalho podem ser expressos como:

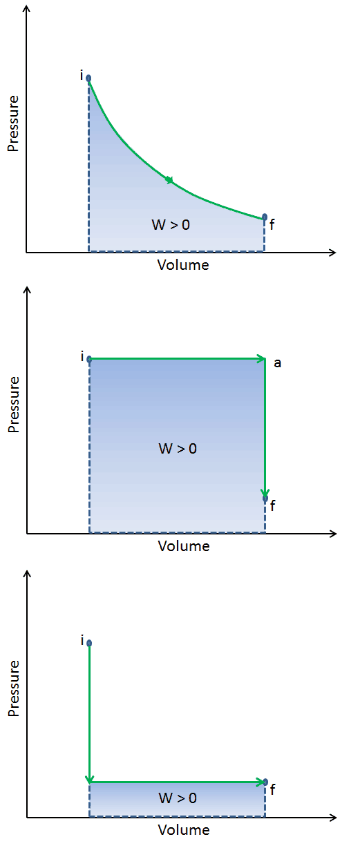
Quando um sistema termodinâmico muda de um estado inicial para um estado final , ele passa por uma série de estados intermediários . Chamamos essa série de estados de caminho . Sempre existem infinitas possibilidades para esses estados intermediários. Quando todos eles são estados de equilíbrio, o caminho pode ser plotado em um diagrama pV . Uma das conclusões mais importantes é que:

O trabalho realizado pelo sistema depende não apenas dos estados inicial e final, mas também dos estados intermediários – ou seja, no caminho.

Q e W são dependentes do caminho, enquanto ΔE _int é independente do caminho. Como pode ser visto na figura (diagrama pV), o trabalho é variável dependente do caminho. A área azul representa o trabalho pΔV realizado por um sistema, que passa de um estado inicial i para um estado final f. O trabalho W é positivo porque o volume do sistema aumenta. O segundo processo mostra que o trabalho é maior e depende do caminho do processo.

Além disso, podemos conduzir o sistema através de uma série de estados formando um circuito fechado , como i ⇒ f ⇒ i . Nesse caso, o estado final é o mesmo que o estado inicial , mas o trabalho total realizado pelo sistema não é zero . Um valor positivo para o trabalho indica que o trabalho é realizado pelo sistema em seus arredores. Um valor negativo indica que o trabalho é realizado no sistema por seus arredores.

Exemplo: Trabalho Específico da Turbina

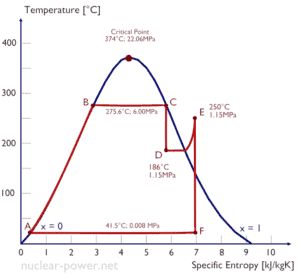
Um estágio de alta pressão da turbina a vapor opera em estado estacionário com condições de entrada de   6 MPa , t = 275,6 ° C , x = 1 (ponto C). Vapor folhas esta etapa de turbina a uma pressão de 1,15 MPa , 186 ° C e x = 0,87 (ponto D). Calcule a diferença de entalpia entre esses dois estados. Determine a transferência de trabalho específica.

A entalpia para o estado C pode ser coletada diretamente das tabelas de vapor , enquanto a entalpia para o estado D deve ser calculada usando a qualidade do vapor :

h _{1, molhado} = 2785 kJ / kg

h _{2, molhado} = h _{2, s} x + (1 – x) h _{2, l}  = 2782. 0,87 + (1 – 0,87). 790 = 2420 + 103 = 2523 kJ / kg

Δh = 262 kJ / kg

Como no processo adiabático dh = dw , Δh = 262 kJ / kg é o trabalho específico da turbina .

Quatro Casos Especiais da Primeira Lei da Termodinâmica

A primeira lei da termodinâmica encontra aplicação em vários casos especiais:

Processo adiabático:

Um processo adiabático é aquele em que não há transferência de calor para dentro ou para fora do sistema. Ocorre muito rapidamente ou um sistema está bem isolado que não ocorre transferência de energia como calor entre o sistema e seu ambiente. Portanto, dQ = 0 na primeira lei da termodinâmica, que é então:

dQ = 0, dE _int = – dW

Processo isocórico:

Um processo isocórico é aquele em que não há alteração no volume . Um processo isocórico é um processo de volume constante. Quando o volume de um sistema termodinâmico é constante, ele não funciona nos seus arredores. Portanto, dW = 0 na primeira lei da termodinâmica, que é então:

dW = 0, dE _int = dQ

Em um processo isocórico , toda a energia adicionada como calor (ou seja, Q é positiva) permanece no sistema como um aumento da energia interna ( aumento da temperatura ).

Processo cíclico:

Um processo que eventualmente retorna um sistema ao seu estado inicial é chamado de processo cíclico . Na conclusão de um ciclo, todas as propriedades têm o mesmo valor que tinham no início.

Para esse processo, o estado final é o mesmo que o estado inicial e, portanto, a mudança total de energia interna deve ser zero . O vapor (água) que circula através de um circuito fechado de resfriamento sofre um ciclo. A primeira lei da termodinâmica é então:

dE _int = 0, dQ = dW

Assim, o trabalho líquido realizado durante o processo deve ser exatamente igual à quantidade líquida de energia transferida como calor.

Expansão livre:

Esse é um  processo adiabático no qual nenhuma transferência de calor ocorre entre o sistema e seu ambiente e nenhum trabalho é realizado no sistema. Esses tipos de processos adiabáticos são chamados de expansão livre . É um processo irreversível no qual um gás se expande para uma câmara evacuada isolada. É também chamado de expansão Joule . Para um gás ideal, a temperatura não muda (consulte: Segunda Lei de Joule ), no entanto, gases reais sofrem uma mudança de temperatura durante a expansão livre. Na expansão livre Q = W = 0, e a primeira lei exige que:

dE _int = 0

Uma expansão livre não pode ser plotada em um diagrama PV, porque o processo é rápido, não quase estático. Os estados intermediários não são estados de equilíbrio e, portanto, a pressão não está claramente definida.