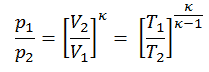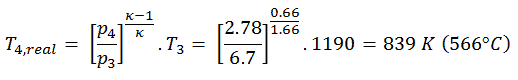Processo Adiabático
Um processo adiabático é um processo termodinâmico , no qual não há transferência de calor para dentro ou para fora do sistema (Q = 0). O sistema pode ser considerado perfeitamente isolado . Em um processo adiabático, a energia é transferida apenas como trabalho. A suposição de que não há transferência de calor é muito importante, pois podemos usar a aproximação adiabática apenas em processos muito rápidos . Nesses processos rápidos, não há tempo suficiente para que a transferência de energia como calor ocorra de ou para o sistema.
Em dispositivos reais (como turbinas, bombas e compressores) ocorrem perdas e perdas de calor no processo de combustão, mas essas perdas são geralmente baixas em comparação com o fluxo geral de energia e podemos aproximar alguns processos termodinâmicos pelo processo adiabático.
Processo Adiabático e a Primeira Lei
Para um sistema fechado, podemos escrever a primeira lei da termodinâmica em termos de entalpia :
dH = dQ + Vdp
Nesta equação, o termo Vdp é um trabalho de processo de fluxo . Este trabalho, Vdp, é usado para sistemas de fluxo aberto, como uma turbina ou uma bomba na qual existe um “dp”, ou seja, mudança de pressão. Como pode ser visto, essa forma de lei simplifica a descrição da transferência de energia . No processo adiabático, a mudança de entalpia é igual ao trabalho do processo de fluxo realizado no ou pelo sistema:
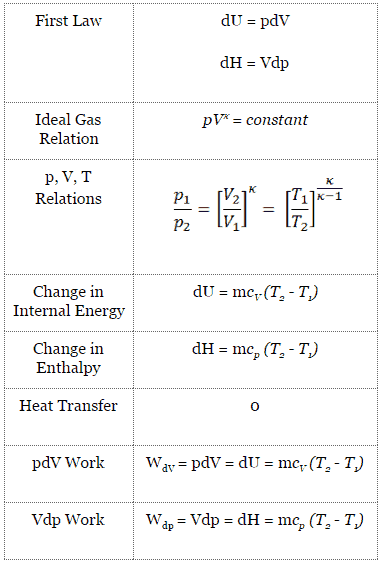
Veja também: Primeira lei da termodinâmica
Veja também: Lei do gás ideal
Veja também: O que é entalpia
Expansão Adiabática – Compressão Adiabática
Veja também: O que é um gás ideal
Num gás ideal , as moléculas não têm volume e não interagem. De acordo com a lei ideal dos gases , a pressão varia linearmente com a temperatura e a quantidade e inversamente com o volume .
pV = nRT
Onde:
- p é a pressão absoluta do gás
- n é a quantidade de substância
- T é a temperatura absoluta
- V é o volume
- R é a constante de gás ideal, ou universal, igual ao produto da constante de Boltzmann e da constante de Avogadro,
Nesta equação, o símbolo R é uma constante chamada constante universal de gás que tem o mesmo valor para todos os gases – ou seja, R = 8,31 J / mol K.
O processo adiabático pode ser expresso com a lei do gás ideal como:
pV κ = constante
ou
p 1 V 1 k = p 2 V 2 k
em que κ = c p / c v é a proporção de aquecimentos específicos (ou capacidades de calor ) para o gás. Um para pressão constante (c p ) e outro para volume constante (c v ) . Observe que essa razão κ = c p / c v é um fator na determinação da velocidade do som em um gás e em outros processos adiabáticos.
Outra relação p, V, T
Em um diagrama de pV , o processo ocorre ao longo de uma linha (chamada adiabat ) que possui a equação p = constante / V κ . Para um gás ideal e um processo politrópico, o caso n = κ corresponde a um processo adiabático.
Exemplo de expansão adiabática
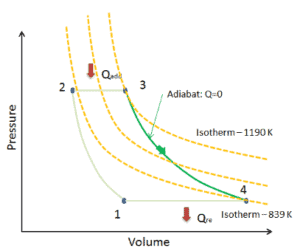
Assuma uma expansão adiabática de hélio ( 3 → 4 ) em uma turbina a gás . Como o hélio se comporta quase como um gás ideal , use a lei do gás ideal para calcular a temperatura de saída do gás ( T 4, real ). Nessas turbinas, o estágio de alta pressão recebe gás (ponto 3 na figura; p 3 = 6,7 MPa ; T 3 = 1190 K (917 ° C)) de um trocador de calor e o esgota em outro trocador de calor, onde a pressão de saída é p 4 = 2,78 MPa (ponto 4) .
Solução:
A temperatura de saída do gás, T4 , real , pode ser calculada usando a relação p, V, T para um processo adiabático. Observe que, é a mesma relação do processo isentrópico , portanto, os resultados devem ser idênticos. Nesse caso, calculamos a expansão para diferentes turbinas a gás (menos eficientes), como no caso da expansão isentrópica na turbina a gás.
Nesta equação, o fator para o hélio é igual a κ = c p / c v = 1,66 . A partir da equação anterior, segue que a temperatura de saída do gás, T4 , real , é:
Veja também: Relação de Mayer
Processo adiabático em turbina a gás

Vamos assumir o ciclo de Brayton que descreve o funcionamento de um motor de calor com pressão constante . Os modernos motores de turbina a gás e os motores a jato de respiração também seguem o ciclo de Brayton.
O ciclo de Brayton consiste em quatro processos termodinâmicos. Dois processos adiabáticos e dois processos isobáricos.
- compressão adiabática – o ar ambiente é aspirado para o compressor, onde é pressurizado (1 → 2). O trabalho necessário para o compressor é dado por W C = H 2 – H 1 .
- adição de calor isobárico – o ar comprimido passa por uma câmara de combustão, onde o combustível é queimado e o ar ou outro meio é aquecido (2 → 3). É um processo de pressão constante, já que a câmara está aberta para entrar e sair. O calor líquido adicionado é dado por Q add = H 3 – H 2
- expansão adiabática – o ar aquecido e pressurizado se expande na turbina, gasta sua energia. O trabalho realizado pela turbina é dado por W T = H 4 – H 3
- rejeição de calor isobárica – o calor residual deve ser rejeitado para fechar o ciclo. O calor líquido rejeitado é dado por Q re = H 4 – H 1
Como pode ser visto, podemos descrever e calcular (por exemplo, eficiência térmica ) esses ciclos (da mesma forma para o ciclo de Rankine ) usando entalpias .
Veja também: Eficiência térmica do ciclo de Brayton
Eficiência isentrópica – turbina, compressor, bocal
Nos capítulos anteriores assumiu-se que a expansão do gás é isentrópica e, portanto, utilizou-se o t 4, é como a temperatura de saída do gás. Essas premissas são aplicáveis apenas aos ciclos ideais.
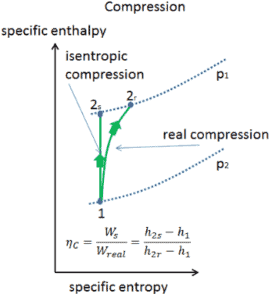
A maioria dos dispositivos de fluxo constante (turbinas, compressores, bicos) opera em condições adiabáticas , mas não são verdadeiramente isentrópicos, mas são idealizados como isentrópicos para fins de cálculo. Definimos os parâmetros η T , η C , η N , como uma razão entre o trabalho real realizado por dispositivo e o trabalho por dispositivo quando operado em condições isentrópicas (no caso de turbinas). Essa relação é conhecida como eficiência isentrópica de turbina / compressor / bico .
Esses parâmetros descrevem com que eficiência uma turbina, compressor ou bico se aproxima de um dispositivo isentrópico correspondente. Este parâmetro reduz a eficiência geral e a produção do trabalho. Para turbinas, o valor de η T é tipicamente de 0,7 a 0,9 (70-90%).
Exemplo: Eficiência isentrópica da turbina
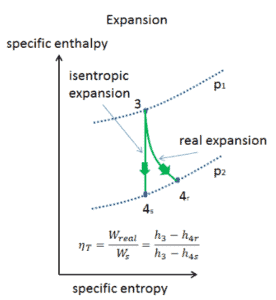
Assuma uma expansão isentrópica de hélio (3 → 4) em uma turbina a gás. Nessas turbinas, o estágio de alta pressão recebe gás (ponto 3 na figura; p 3 = 6,7 MPa ; T 3 = 1190 K (917 ° C)) de um trocador de calor e o esgota em outro trocador de calor, onde a pressão de saída é p 4 = 2,78 MPa (ponto 4) . A temperatura (para o processo isentrópico) do gás na saída da turbina é T 4s = 839 K (566 ° C).
Calcule o trabalho realizado por esta turbina e calcule a temperatura real na saída da turbina, quando a eficiência isentrópica da turbina for η T = 0,91 (91%) .
Solução:
A partir da primeira lei da termodinâmica, o trabalho realizado pela turbina em um processo isentrópico pode ser calculado a partir de:
W T = h 3 – h 4s → W Ts = c p (T 3 – T 4s )
Pela Lei do Gás Ideal, sabemos que o calor molar específico de um gás ideal monatômico é:
C v = 3 / 2R = 12,5 J / mol K e C p = C v + R = 5 / 2R = 20,8 J / mol K
Transferimos as capacidades de calor específicas em unidades de J / kg K via:
c p = C p . 1 / M (peso molar de hélio) = 20,8 x 4,10 -3 = 5200 J / kg K
O trabalho realizado pela turbina a gás no processo isentrópico é então:
W T, s = c p ( T3 – T4s ) = 5200 x (1190 – 839) = 1,825 MJ / kg
O trabalho real realizado pela turbina a gás no processo adiabático é então:
WT , real = cp ( T3 – T4s ). η T = 5200 x (1190 – 839) x 0,91 = 1,661 MJ / kg
Expansão Livre – Expansão Joule
Esses são processos adiabáticos nos quais nenhuma transferência de calor ocorre entre o sistema e seu ambiente e nenhum trabalho é realizado no sistema. Esses tipos de processos adiabáticos são chamados de expansão livre . É um processo irreversível no qual um gás se expande para uma câmara evacuada isolada. É também chamado de expansão Joule . Para um gás ideal, a temperatura não muda (consulte: Segunda Lei de Joule ), no entanto, gases reais sofrem uma mudança de temperatura durante a expansão livre. Na expansão livre Q = W = 0, e a primeira lei exige que:
dE int = 0
Uma expansão livre não pode ser plotada em um diagrama PV, porque o processo é rápido, não quase estático. Os estados intermediários não são estados de equilíbrio e, portanto, a pressão não está claramente definida.
……………………………………………………………………………………………………………………………….
Este artigo é baseado na tradução automática do artigo original em inglês. Para mais informações, consulte o artigo em inglês. Você pode nos ajudar. Se você deseja corrigir a tradução, envie-a para: translations@nuclear-power.com ou preencha o formulário de tradução on-line. Agradecemos sua ajuda, atualizaremos a tradução o mais rápido possível. Obrigado.