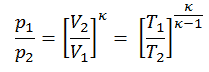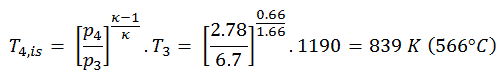Processo isentrópico
Um processo isentrópico é um processo termodinâmico , no qual a entropia do fluido ou gás permanece constante. Isso significa que o processo isentrópico é um caso especial de um processo adiabático no qual não há transferência de calor ou matéria. É um processo adiabático reversível . Um processo isentrópico também pode ser chamado de processo de entropia constante. Na engenharia, esse processo idealizado é muito útil para comparação com processos reais.
Como existem mudanças na energia interna (dU) e no volume do sistema (∆V), os engenheiros costumam usar a entalpia do sistema, que é definida como:
H = U + pV
Em muitas análises termodinâmicas, é conveniente usar a entalpia em vez da energia interna. Especialmente no caso da primeira lei da termodinâmica .
Processo isentrópico e a primeira lei
A primeira lei da termodinâmica em termos de entalpia :
dH = dQ + Vdp
ou
dH = TdS + Vdp

Veja também: Primeira lei da termodinâmica
Veja também: Lei do gás ideal
Veja também: O que é entalpia
dH = Vdp → W = H 2 – H 1 → H 2 – H 1 = C P (T 2 – T 1 ) (para gás ideal )
Expansão Isentrópica – Compressão Isentrópica
Veja também: O que é um gás ideal
Num gás ideal , as moléculas não têm volume e não interagem. De acordo com a lei ideal dos gases , a pressão varia linearmente com a temperatura e a quantidade e inversamente com o volume .
pV = nRT
Onde:
- p é a pressão absoluta do gás
- n é a quantidade de substância
- T é a temperatura absoluta
- V é o volume
- R é a constante de gás ideal, ou universal, igual ao produto da constante de Boltzmann e da constante de Avogadro,
Nesta equação, o símbolo R é uma constante chamada constante universal de gás que tem o mesmo valor para todos os gases – ou seja, R = 8,31 J / mol K.
O processo isentrópico (um caso especial de processo adiabático) pode ser expresso com a lei dos gases ideais como:
pV κ = constante
ou
p 1 V 1 k = p 2 V 2 k
em que κ = c p / c v é a proporção de aquecimentos específicos (ou capacidades de calor ) para o gás. Um para pressão constante (c p ) e outro para volume constante (c v ) . Observe que essa razão κ = c p / c v é um fator na determinação da velocidade do som em um gás e em outros processos adiabáticos.
Outra relação p, V, T
Em um diagrama de pV , o processo ocorre ao longo de uma linha (chamada adiabat ) que possui a equação p = constante / V κ . Para um gás ideal e um processo politrópico, o caso n = κ corresponde a um processo isentrópico.
Exemplo: Expansão Isentrópica na Turbina a Gás
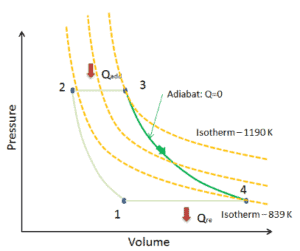
Assuma uma expansão isentrópica de hélio ( 3 → 4 ) em uma turbina a gás . Como o hélio se comporta quase como um gás ideal , use a lei do gás ideal para calcular a temperatura de saída do gás ( T 4, é ). Nessas turbinas, o estágio de alta pressão recebe gás (ponto 3 na figura; p 3 = 6,7 MPa ; T 3 = 1190 K (917 ° C)) de um trocador de calor e o esgota em outro trocador de calor, onde a pressão de saída é p 4 = 2,78 MPa (ponto 4) .
Solução:
A temperatura de saída do gás, T 4, é , pode ser calculada usando a relação p, V, T para o processo isentrópico (processo adiabático reversível):
Nesta equação, o fator para o hélio é igual a κ = c p / c v = 1,66 . A partir da equação anterior, segue que a temperatura de saída do gás, T 4 , é:
Exemplo: Expansão Isentrópica na Turbina a Gás

Vamos assumir o ciclo de Brayton ideal que descreve o funcionamento de um motor de calor com pressão constante . Os modernos motores de turbina a gás e os motores a jato de respiração também seguem o ciclo de Brayton.
O ciclo ideal de Brayton consiste em quatro processos termodinâmicos. Dois processos isentrópicos e dois processos isobáricos.
- compressão isentrópica – o ar ambiente é aspirado para o compressor, onde é pressurizado (1 → 2). O trabalho necessário para o compressor é dado por W C = H 2 – H 1 .
- adição de calor isobárico – o ar comprimido passa por uma câmara de combustão, onde o combustível é queimado e o ar ou outro meio é aquecido (2 → 3). É um processo de pressão constante, já que a câmara está aberta para entrar e sair. O calor líquido adicionado é dado por Q add = H 3 – H 2
- expansão isentrópica – o ar aquecido e pressurizado se expande na turbina, gasta sua energia. O trabalho realizado pela turbina é dado por W T = H 4 – H 3
- rejeição de calor isobárica – o calor residual deve ser rejeitado para fechar o ciclo. O calor líquido rejeitado é dado por Q re = H 4 – H 1
Como pode ser visto, podemos descrever e calcular (por exemplo, eficiência térmica ) esses ciclos (da mesma forma para o ciclo de Rankine ) usando entalpias .
Veja também: Eficiência térmica do ciclo de Brayton
Processos isentrópicos em ciclos termodinâmicos
Ciclo de Carnot ideal
- Compressão isentrópica
- Expansão isentrópica
Ciclo Rankine Ideal
- Compressão isentrópica em uma bomba
- Expansão isentrópica em uma turbina
Ciclo de Brayton ideal
- Compressão isentrópica em um compressor
- Expansão isentrópica em uma turbina
Ciclo Otto Ideal
- Compressão isentrópica
- Expansão isentrópica
Ciclo Diesel Ideal
- Compressão isentrópica
- Expansão isentrópica
Eficiência isentrópica – turbina, compressor, bocal
Nos capítulos anteriores assumiu-se que a expansão do gás é isentrópica e, portanto, utilizou-se o t 4, é como a temperatura de saída do gás. Essas premissas são aplicáveis apenas aos ciclos ideais.
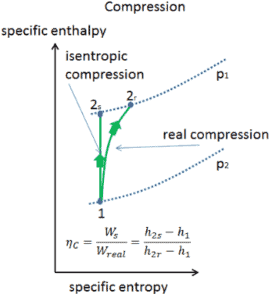
A maioria dos dispositivos de fluxo constante (turbinas, compressores, bicos) opera em condições adiabáticas , mas não são verdadeiramente isentrópicos, mas são idealizados como isentrópicos para fins de cálculo. Definimos os parâmetros η T , η C , η N , como uma razão entre o trabalho real realizado por dispositivo e o trabalho por dispositivo quando operado em condições isentrópicas (no caso de turbinas). Essa relação é conhecida como eficiência isentrópica de turbina / compressor / bico .
Esses parâmetros descrevem com que eficiência uma turbina, compressor ou bico se aproxima de um dispositivo isentrópico correspondente. Este parâmetro reduz a eficiência geral e a produção do trabalho. Para turbinas, o valor de η T é tipicamente de 0,7 a 0,9 (70-90%).
Exemplo: Eficiência isentrópica da turbina
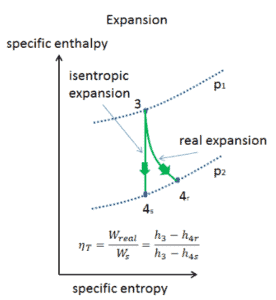
Assuma uma expansão isentrópica de hélio (3 → 4) em uma turbina a gás. Nessas turbinas, o estágio de alta pressão recebe gás (ponto 3 na figura; p 3 = 6,7 MPa ; T 3 = 1190 K (917 ° C)) de um trocador de calor e o esgota em outro trocador de calor, onde a pressão de saída é p 4 = 2,78 MPa (ponto 4) . A temperatura (para o processo isentrópico) do gás na saída da turbina é T 4s = 839 K (566 ° C).
Calcule o trabalho realizado por esta turbina e calcule a temperatura real na saída da turbina, quando a eficiência isentrópica da turbina for η T = 0,91 (91%) .
Solução:
A partir da primeira lei da termodinâmica, o trabalho realizado pela turbina em um processo isentrópico pode ser calculado a partir de:
W T = h 3 – h 4s → W Ts = c p (T 3 – T 4s )
Pela Lei do Gás Ideal, sabemos que o calor molar específico de um gás ideal monatômico é:
C v = 3 / 2R = 12,5 J / mol K e C p = C v + R = 5 / 2R = 20,8 J / mol K
Transferimos as capacidades de calor específicas em unidades de J / kg K via:
c p = C p . 1 / M (peso molar de hélio) = 20,8 x 4,10 -3 = 5200 J / kg K
O trabalho realizado pela turbina a gás no processo isentrópico é então:
W T, s = c p ( T3 – T4s ) = 5200 x (1190 – 839) = 1,825 MJ / kg
O trabalho real realizado pela turbina a gás no processo adiabático é então:
WT , real = cp ( T3 – T4s ). η T = 5200 x (1190 – 839) x 0,91 = 1,661 MJ / kg
……………………………………………………………………………………………………………………………….
Este artigo é baseado na tradução automática do artigo original em inglês. Para mais informações, consulte o artigo em inglês. Você pode nos ajudar. Se você deseja corrigir a tradução, envie-a para: translations@nuclear-power.com ou preencha o formulário de tradução on-line. Agradecemos sua ajuda, atualizaremos a tradução o mais rápido possível. Obrigado.