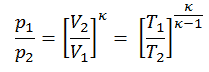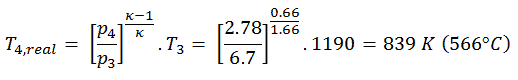Processus adiabatique
Un processus adiabatique est un processus thermodynamique , dans lequel il n’y a pas de transfert de chaleur dans ou hors du système (Q = 0). Le système peut être considéré comme parfaitement isolé . Dans un processus adiabatique, l’énergie n’est transférée que sous forme de travail. L’hypothèse d’absence de transfert de chaleur est très importante, car nous ne pouvons utiliser l’approximation adiabatique que dans des processus très rapides . Dans ces processus rapides, il n’y a pas assez de temps pour que le transfert d’énergie sous forme de chaleur ait lieu vers ou depuis le système.
Dans les appareils réels (tels que les turbines, les pompes et les compresseurs), des pertes de chaleur et des pertes dans le processus de combustion se produisent, mais ces pertes sont généralement faibles par rapport au flux d’énergie global et nous pouvons approximer certains processus thermodynamiques par le processus adiabatique.
Processus adiabatique et première loi
Pour un système fermé, on peut écrire la première loi de la thermodynamique en termes d’enthalpie :
dH = dQ + Vdp
Dans cette équation, le terme Vdp est un travail de processus d’écoulement . Ce travail, Vdp, est utilisé pour des systèmes à flux ouvert comme une turbine ou une pompe dans lesquels il y a un «dp», c’est-à-dire un changement de pression. Comme on peut le voir, cette forme de loi simplifie la description du transfert d’énergie . Dans le processus adiabatique, le changement d’enthalpie est égal au travail du processus d’écoulement effectué sur ou par le système:
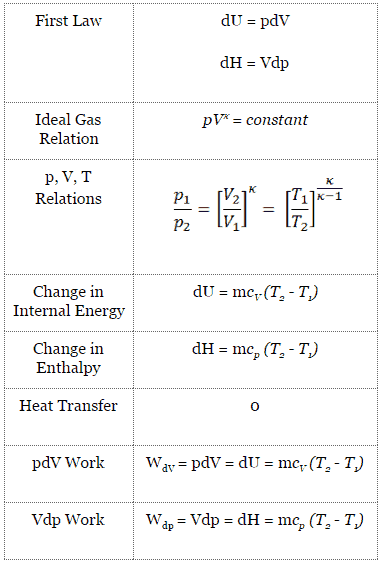
Voir aussi: Première loi de la thermodynamique
Voir aussi: Loi sur les gaz parfaits
Voir aussi: Qu’est-ce que l’enthalpie
Expansion adiabatique – Compression adiabatique
Voir aussi: Qu’est-ce qu’un gaz parfait
Dans un gaz parfait , les molécules n’ont pas de volume et n’interagissent pas. Selon la loi du gaz parfait , la pression varie linéairement avec la température et la quantité, et inversement avec le volume .
pV = nRT
où:
- p est la pression absolue du gaz
- n est la quantité de substance
- T est la température absolue
- V est le volume
- R est la constante de gaz parfaite ou universelle, égale au produit de la constante de Boltzmann et de la constante d’Avogadro,
Dans cette équation, le symbole R est une constante appelée constante de gaz universelle qui a la même valeur pour tous les gaz, à savoir R = 8,31 J / mol K.
Le processus adiabatique peut s’exprimer avec la loi du gaz parfait comme:
pV κ = constant
ou
p 1 V 1 κ = p 2 V 2 κ
dans laquelle κ = c p / c v est le rapport des chaleurs spécifiques (ou capacités calorifiques ) pour le gaz. Un pour une pression constante (c p ) et un pour un volume constant (c v ) . Notez que ce rapport κ = c p / c v est un facteur déterminant la vitesse du son dans un gaz et d’autres processus adiabatiques.
Autre relation p, V, T
Sur un diagramme pV , le processus se produit le long d’une ligne (appelée adiabat ) qui a l’équation p = constante / V κ . Pour un gaz parfait et un processus polytropique, le cas n = κ correspond à un processus adiabatique.
Exemple d’expansion adiabatique
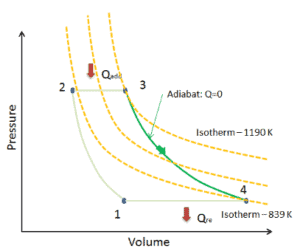
Supposons une expansion adiabatique d’hélium ( 3 → 4 ) dans une turbine à gaz . L’hélium se comportant presque comme un gaz parfait , utilisez la loi du gaz parfait pour calculer la température de sortie du gaz ( T 4, réel ). Dans ces turbines, l’étage haute pression reçoit du gaz (point 3 sur la figure; p 3 = 6,7 MPa ; T 3 = 1190 K (917 ° C)) d’un échangeur de chaleur et l’évacue vers un autre échangeur de chaleur, où la pression de sortie est p 4 = 2,78 MPa (point 4) .
Solution:
La température de sortie du gaz, T 4, réel , peut être calculée en utilisant la relation p, V, T pour le processus adiabatique. Notez que, c’est la même relation que pour le processus isentropique , donc les résultats doivent être identiques. Dans ce cas, nous calculons l’expansion pour différentes turbines à gaz (moins efficaces) comme dans le cas d’une expansion isentropique dans une turbine à gaz.
Dans cette équation, le facteur pour l’hélium est égal à κ = c p / c v = 1,66 . Il résulte de l’équation précédente que la température de sortie du gaz, T 4, réel , est:
Voir aussi: la relation de Mayer
Processus adiabatique dans les turbines à gaz

Supposons le cycle de Brayton qui décrit le fonctionnement d’un moteur thermique à pression constante . Les moteurs à turbine à gaz modernes et les moteurs à réaction à respiration aérodynamique suivent également le cycle de Brayton.
Le cycle de Brayton comprend quatre processus thermodynamiques. Deux processus adiabatiques et deux processus isobares.
- compression adiabatique – l’air ambiant est aspiré dans le compresseur, où il est mis sous pression (1 → 2). Le travail requis pour le compresseur est donné par W C = H 2 – H 1 .
- addition de chaleur isobare – l’air comprimé traverse ensuite une chambre de combustion, où le combustible est brûlé et l’air ou un autre milieu est chauffé (2 → 3). Il s’agit d’un processus à pression constante, car la chambre est ouverte pour entrer et sortir. La chaleur nette ajoutée est donnée par Q add = H 3 – H 2
- expansion adiabatique – l’air chauffé sous pression se détend ensuite sur la turbine, cède son énergie. Le travail effectué par turbine est donné par W T = H 4 – H 3
- rejet de chaleur isobare – la chaleur résiduelle doit être rejetée afin de fermer le cycle. La chaleur nette rejetée est donnée par Q re = H 4 – H 1
Comme on peut le voir, nous pouvons décrire et calculer (par exemple l’ efficacité thermique ) de tels cycles (de même pour le cycle de Rankine ) en utilisant des enthalpies .
Voir aussi: Efficacité thermique du cycle de Brayton
Efficacité isentropique – Turbine, compresseur, buse
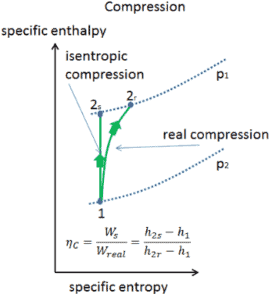
Dans les chapitres précédents, nous avons supposé que l’expansion du gaz est isentropique et, par conséquent, nous avons utilisé T 4, soit la température de sortie du gaz. Ces hypothèses ne sont applicables qu’avec des cycles idéaux.
La plupart des dispositifs à flux constant (turbines, compresseurs, buses) fonctionnent dans des conditions adiabatiques , mais ils ne sont pas vraiment isentropiques mais sont plutôt idéalisés comme isentropiques à des fins de calcul. Nous définissons les paramètres η T , η C , η N , comme un rapport entre le travail réel effectué par appareil et le travail par appareil lorsqu’il est utilisé dans des conditions isentropiques (dans le cas d’une turbine). Ce rapport est connu sous le nom d’ efficacité turbine isentropique / compresseur / buse .
Ces paramètres décrivent l’efficacité avec laquelle une turbine, un compresseur ou une buse se rapproche d’un dispositif isentropique correspondant. Ce paramètre réduit l’efficacité globale et le rendement de travail. Pour les turbines, la valeur de η T est généralement de 0,7 à 0,9 (70–90%).
Exemple: efficacité de la turbine isentropique
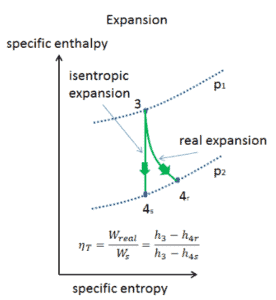
Supposons une expansion isentropique de l’hélium (3 → 4) dans une turbine à gaz. Dans ces turbines, l’étage haute pression reçoit du gaz (point 3 sur la figure; p 3 = 6,7 MPa ; T 3 = 1190 K (917 ° C)) d’un échangeur de chaleur et l’évacue vers un autre échangeur de chaleur, où la pression de sortie est p 4 = 2,78 MPa (point 4) . La température (pour le processus isentropique) du gaz à la sortie de la turbine est T 4s = 839 K (566 ° C).
Calculez le travail effectué par cette turbine et calculez la température réelle à la sortie de la turbine, lorsque le rendement de la turbine isentropique est η T = 0,91 (91%) .
Solution:
A partir de le première principe de la thermodynamique, le travail effectué par turbine dans un processus isentropique peut être calculé à partir de:
W T = h 3 – h 4s → W Ts = c p (T 3 – T 4s )
D’après la loi des gaz parfaits, nous savons que la chaleur spécifique molaire d’un gaz parfait monoatomique est:
C v = 3 / 2R = 12,5 J / mol K et C p = C v + R = 5 / 2R = 20,8 J / mol K
Nous transférons les capacités calorifiques spécifiques en unités de J / kg K via:
c p = C p . 1 / M (poids molaire de l’hélium) = 20,8 x 4,10 -3 = 5200 J / kg K
Le travail effectué par turbine à gaz en procédé isentropique est alors:
W T, s = c p (T 3 – T 4s ) = 5200 x (1190 – 839) = 1,825 MJ / kg
Le travail réel effectué par la turbine à gaz en processus adiabatique est alors:
W T, réel = c p (T 3 – T 4s ). η T = 5200 x (1190 – 839) x 0,91 = 1,661 MJ / kg
Expansion gratuite – Expansion Joule
Ce sont des processus adiabatiques dans lesquels aucun transfert de chaleur ne se produit entre le système et son environnement et aucun travail n’est effectué sur ou par le système. Ces types de processus adiabatiques sont appelés expansion libre . Il s’agit d’un processus irréversible dans lequel un gaz se détend dans une chambre sous vide isolée. Il est également appelé expansion Joule . Pour un gaz parfait, la température ne change pas (voir: Deuxième loi de Joule ), cependant, les vrais gaz subissent un changement de température pendant la détente libre. En expansion libre Q = W = 0, et le première principe exige que:
dE int = 0
Une expansion libre ne peut pas être tracée sur un diagramme PV, car le processus est rapide et non quasi statique. Les états intermédiaires ne sont pas des états d’équilibre, et donc la pression n’est pas clairement définie.
……………………………………………………………………………………………………………………………….
Cet article est basé sur la traduction automatique de l’article original en anglais. Pour plus d’informations, voir l’article en anglais. Pouvez vous nous aider Si vous souhaitez corriger la traduction, envoyez-la à l’adresse: translations@nuclear-power.com ou remplissez le formulaire de traduction en ligne. Nous apprécions votre aide, nous mettrons à jour la traduction le plus rapidement possible. Merci