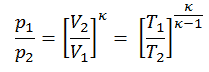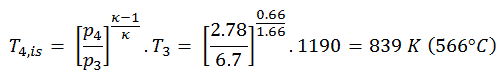Isentropischer Prozess
Ein isentropischer Prozess ist ein thermodynamischer Prozess , bei dem die Entropie des Fluids oder Gases konstant bleibt. Dies bedeutet, dass der isentrope Prozess ein Sonderfall eines adiabatischen Prozesses ist, bei dem keine Wärme- oder Materieübertragung stattfindet. Es ist ein reversibler adiabatischer Prozess . Ein isentropischer Prozess kann auch als konstanter Entropieprozess bezeichnet werden. In der Technik ist ein solcher idealisierter Prozess sehr nützlich für den Vergleich mit realen Prozessen.
Da sich die innere Energie (dU) und das Systemvolumen (∆V) ändern, verwenden Ingenieure häufig die Enthalpie des Systems, die wie folgt definiert ist:
H = U + pV
In vielen thermodynamischen Analysen ist es zweckmäßig, die Enthalpie anstelle der inneren Energie zu verwenden. Besonders im Fall des ersten Hauptsatzes der Thermodynamik .
Isentropischer Prozess und das erste Gesetz
Der erste Hauptsatz der Thermodynamik in Bezug auf die Enthalpie :
dH = dQ + Vdp
oder
dH = TdS + Vdp

Siehe auch: Erster Hauptsatz der Thermodynamik
Siehe auch: Ideales Gasgesetz
Siehe auch: Was ist Enthalpie?
dH = Vdp → W = H 2 – H 1 → H 2 – H 1 = C p (T 2 – T 1 ) (für ideales Gas )
Isentropische Expansion – Isentropische Kompression
Siehe auch: Was ist ein ideales Gas?
In einem idealen Gas haben Moleküle kein Volumen und interagieren nicht. Nach dem idealen Gasgesetz ändert sich der Druck linear mit Temperatur und Menge und umgekehrt mit dem Volumen .
pV = nRT
wo:
- p ist der absolute Druck des Gases
- n ist die Substanzmenge
- T ist die absolute Temperatur
- V ist die Lautstärke
- R ist die ideale oder universelle Gaskonstante, die dem Produkt der Boltzmann-Konstante und der Avogadro-Konstante entspricht.
In dieser Gleichung ist das Symbol R eine Konstante, die als universelle Gaskonstante bezeichnet wird und für alle Gase den gleichen Wert hat, nämlich R = 8,31 J / mol K.
Der isentrope Prozess (ein Sonderfall des adiabatischen Prozesses) kann mit dem idealen Gasgesetz ausgedrückt werden als:
pV κ = konstant
oder
p 1 V 1 κ = p 2 V 2 κ
wobei κ = c p / c v das Verhältnis der spezifischen Wärme (oder Wärmekapazitäten ) für das Gas ist. Eine für konstanten Druck (c p ) und eine für konstantes Volumen (c v ) . Es ist zu beachten, dass dieses Verhältnis κ = c p / c v ein Faktor bei der Bestimmung der Schallgeschwindigkeit in einem Gas und anderen adiabatischen Prozessen ist.
Andere p, V, T-Beziehung
In einem pV-Diagramm erfolgt der Prozess entlang einer Linie ( Adiabat genannt ) mit der Gleichung p = Konstante / V κ . Für ein ideales Gas und einen polytropischen Prozess entspricht der Fall n = κ einem isentropischen Prozess.
Beispiel: Isentropische Expansion in Gasturbinen
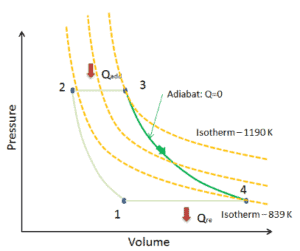
Nehmen Sie eine isentrope Expansion von Helium ( 3 → 4 ) in einer Gasturbine an . Da sich Helium fast wie ein ideales Gas verhält , verwenden Sie das ideale Gasgesetz , um die Austrittstemperatur des Gases zu berechnen ( T 4, ist ). In diesen Turbinen erhält die Hochdruckstufe Gas (Punkt 3 in der Abbildung; p 3 = 6,7 MPa ; T 3 = 1190 K (917 ° C)) von einem Wärmetauscher und leitet es an einen anderen Wärmetauscher ab, wo der Ausgangsdruck beträgt ist p 4 = 2,78 MPa (Punkt 4) .
Lösung:
Die Austrittstemperatur des Gases T 4 kann unter Verwendung von p, V, T berechnet werden. Beziehung für isentropischen Prozess (reversibler adiabatischer Prozess):
In dieser Gleichung ist der Faktor für Helium gleich κ = c p / c v = 1,66 . Aus der vorhergehenden Gleichung folgt, dass die Austrittstemperatur des Gases T 4 ist:
Beispiel: Isentropische Expansion in Gasturbinen

Nehmen wir den idealen Brayton-Zyklus an , der die Funktionsweise einer Wärmekraftmaschine mit konstantem Druck beschreibt . Moderne Gasturbinentriebwerke und luftatmende Strahltriebwerke folgen ebenfalls dem Brayton-Zyklus.
Der ideale Brayton-Zyklus besteht aus vier thermodynamischen Prozessen. Zwei isentrope Prozesse und zwei isobare Prozesse.
- isentropische Kompression – Umgebungsluft wird in den Kompressor gesaugt und dort unter Druck gesetzt (1 → 2). Die für den Kompressor erforderliche Arbeit ist gegeben durch W C = H 2 – H 1 .
- isobare Wärmezufuhr – Die Druckluft strömt dann durch eine Brennkammer, in der Kraftstoff verbrannt und Luft oder ein anderes Medium erwärmt wird (2 → 3). Es ist ein Prozess mit konstantem Druck, da die Kammer zum Ein- und Ausströmen geöffnet ist. Die hinzugefügte Nettowärme ist gegeben durch Q add = H 3 – H 2
- isentropische Expansion – Die erwärmte Druckluft dehnt sich dann auf der Turbine aus und gibt ihre Energie ab. Die von der Turbine geleistete Arbeit ist gegeben durch W T = H 4 – H 3
- isobare Wärmeabgabe – Die Restwärme muss abgeführt werden, um den Kreislauf zu schließen. Die abgegebene Nettowärme ist gegeben durch Q re = H 4 – H 1
Wie zu sehen ist, können wir solche Kreisprozessen (ähnlich für den Rankine-Zyklus ) unter Verwendung von Enthalpien beschreiben und berechnen (z. B. thermische Effizienz ) .
Siehe auch: Thermische Effizienz des Brayton-Zyklus
Isentrope Prozesse in thermodynamischen Kreisprozessen
Idealer Carnot-Zyklus
- Isentropische Kompression
- Isentropische Expansion
Idealer Rankine-Zyklus
- Isentrope Kompression in einer Pumpe
- Isentropische Expansion in einer Turbine
Idealer Brayton-Zyklus
- Isentropische Kompression in einem Kompressor
- Isentropische Expansion in einer Turbine
Idealer Otto-Zyklus
- Isentropische Kompression
- Isentropische Expansion
Idealer Dieselzyklus
- Isentropische Kompression
- Isentropische Expansion
Isentropische Effizienz – Turbine, Kompressor, Düse
In den vorhergehenden Kapiteln haben wir angenommen, dass die Gasexpansion isentrop ist, und deshalb haben wir T 4 als Austrittstemperatur des Gases verwendet. Diese Annahmen gelten nur für ideale Kreisprozessen.
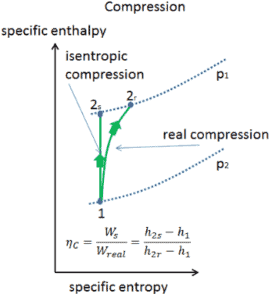
Die meisten Steady-Flow-Geräte (Turbinen, Kompressoren, Düsen) arbeiten unter adiabatischen Bedingungen , sind jedoch nicht wirklich isentrop, sondern für Berechnungszwecke eher als isentrop idealisiert. Wir definieren Parameter η T , η C , η N , als ein Verhältnis der realen Arbeit durch die Vorrichtung zu der Arbeit von Gerät , wenn es unter Bedingungen betrieben isentropen (im Falle der Turbine). Dieses Verhältnis ist als Wirkungsgrad von Isentropenturbine / Kompressor / Düse bekannt .
Diese Parameter beschreiben, wie effizient sich eine Turbine, ein Kompressor oder eine Düse einer entsprechenden isentropischen Vorrichtung annähert. Dieser Parameter reduziert die Gesamteffizienz und die Arbeitsleistung. Für Turbinen beträgt der Wert von η T typischerweise 0,7 bis 0,9 (70–90%).
Beispiel: Wirkungsgrad isentropischer Turbinen
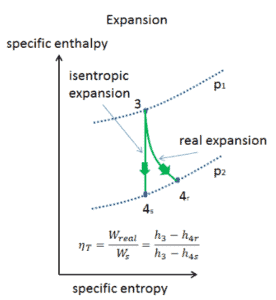
Nehmen Sie eine isentrope Expansion von Helium (3 → 4) in einer Gasturbine an. In diesen Turbinen erhält die Hochdruckstufe Gas (Punkt 3 in der Abbildung; p 3 = 6,7 MPa ; T 3 = 1190 K (917 ° C)) von einem Wärmetauscher und leitet es an einen anderen Wärmetauscher ab, wo der Ausgangsdruck beträgt ist p 4 = 2,78 MPa (Punkt 4) . Die Temperatur (für den isentropischen Prozess) des Gases am Ausgang der Turbine beträgt T 4s = 839 K (566 ° C).
Berechnen Sie die von dieser Turbine geleistete Arbeit und die tatsächliche Temperatur am Ausgang der Turbine, wenn der Wirkungsgrad der isentropischen Turbine η T = 0,91 (91%) beträgt .
Lösung:
Aus dem ersten Hauptsatz der Thermodynamik kann die Arbeit der Turbine in einem isentropischen Prozess berechnet werden aus:
W T = h 3 – h 4 s → W Ts = c p (T 3 – T 4 s )
Aus dem Idealgasgesetz wissen wir, dass die molare spezifische Wärme eines einatomigen Idealgases ist:
C v = 3 / 2R = 12,5 J / mol K und C p = C v + R = 5 / 2R = 20,8 J / mol K.
Wir übertragen die spezifischen Wärmekapazitäten in Einheiten von J / kg K über:
c p = C p . 1 / M (Molgewicht von Helium) = 20,8 · 4,10 & supmin; ³ = 5200 J / kg K.
Die Arbeit der Gasturbine im isentropischen Prozess ist dann:
W T, s = c p (T 3 – T 4 s ) = 5200 × (1190–839) = 1,825 MJ / kg
Die eigentliche Arbeit der Gasturbine im adiabatischen Prozess ist dann:
W T, real = c p (T 3 – T 4s ). η T = 5200 x (1190 – 839) x 0,91 = 1,661 MJ / kg
Dieser Artikel basiert auf der maschinellen Übersetzung des englischen Originalartikels. Weitere Informationen finden Sie im Artikel auf Englisch. Sie können uns helfen. Wenn Sie die Übersetzung korrigieren möchten, senden Sie diese bitte an: translations@nuclear-power.com oder füllen Sie das Online-Übersetzungsformular aus. Wir bedanken uns für Ihre Hilfe und werden die Übersetzung so schnell wie möglich aktualisieren. Danke.