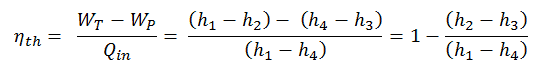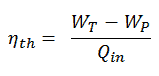Eficiência térmica da turbina a vapor
Em geral, a eficiência térmica , η th , de qualquer motor de calor é definida como a razão entre o trabalho que faz, W , para o calor de entrada a uma temperatura elevada, Q H .
A eficiência térmica , η th , representa a fração de calor , Q H , que é convertida em trabalho . Como a energia é conservada de acordo com a primeira lei da termodinâmica e a energia não pode ser convertida para funcionar completamente, a entrada de calor, Q H , deve ser igual ao trabalho realizado, W, mais o calor que deve ser dissipado como calor residual Q C no meio Ambiente. Portanto, podemos reescrever a fórmula da eficiência térmica como:
Essa é uma fórmula muito útil, mas aqui expressamos a eficiência térmica usando a primeira lei em termos de entalpia .
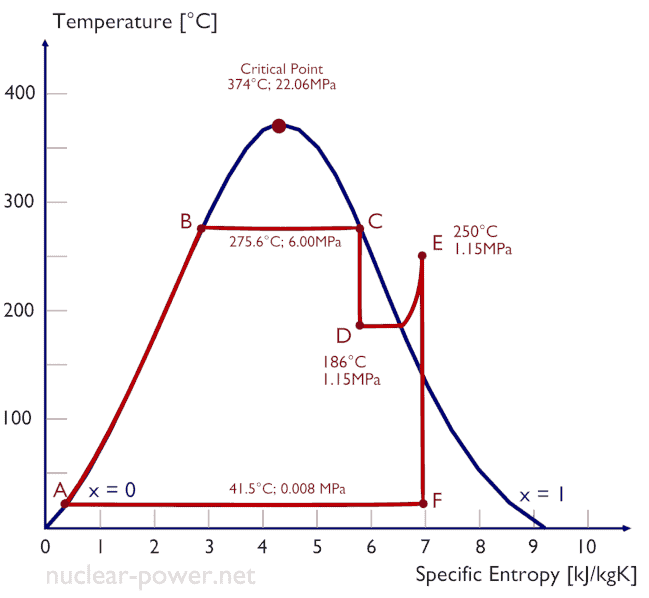
Normalmente, a maioria das usinas nucleares opera turbinas a vapor de condensação de vários estágios . Nessas turbinas, o estágio de alta pressão recebe vapor (esse vapor é quase saturado – x = 0,995 – ponto C na figura; 6 MPa ; 275,6 ° C) de um gerador de vapor e o esgota para o separador-reaquecedor de umidade (ponto D ) O vapor deve ser reaquecido para evitar danos que possam ser causados às pás da turbina a vapor por vapor de baixa qualidade . O reaquecedor aquece o vapor (ponto D) e, em seguida, o vapor é direcionado para o estágio de baixa pressão da turbina a vapor, onde se expande (pontos E a F). O vapor exaurido condensa no condensador e está a uma pressão bem abaixo da atmosférica (pressão absoluta de0,008 MPa ) e está em um estado parcialmente condensado (ponto F), tipicamente com uma qualidade próxima a 90%.
onde a temperatura do reservatório quente é de 275,6 ° C (548,7 K), a temperatura do reservatório frio é de 41,5 ° C (314,7 K). Mas a usina nuclear é o verdadeiro motor térmico , no qual os processos termodinâmicos são de alguma forma irreversíveis. Eles não são feitos infinitamente devagar. Em dispositivos reais (como turbinas, bombas e compressores), um atrito mecânico e perdas de calor causam mais perdas de eficiência.
Para calcular a eficiência térmica do ciclo Rankine mais simples (sem reaquecimento), os engenheiros usam a primeira lei da termodinâmica em termos de entalpia e não em energia interna.
A primeira lei em termos de entalpia é:
dH = dQ + Vdp
Nesta equação, o termo Vdp é um trabalho de processo de fluxo. Este trabalho, Vdp , é usado para sistemas de fluxo aberto, como uma turbina ou uma bomba na qual existe um “dp” , ou seja, mudança de pressão. Não há alterações no volume de controle . Como pode ser visto, essa forma de lei simplifica a descrição da transferência de energia . A pressão constante , a mudança de entalpia é igual à energia transferida do ambiente através do aquecimento:
Processo isobárico (Vdp = 0):
dH = dQ → Q = H 2 – H 1
Na entropia constante , ou seja, no processo isentrópico, a mudança de entalpia é igual ao trabalho do processo de fluxo realizado no ou pelo sistema:
Processo isentrópico (dQ = 0):
dH = Vdp → W = H 2 – H 1
É óbvio que será muito útil na análise de ambos os ciclos termodinâmicos usados na engenharia de energia, ou seja, no ciclo de Brayton e no ciclo de Rankine.
A entalpia pode ser transformada em uma variável intensiva ou específica dividindo-se pela massa . Os engenheiros usam mais a entalpia específica na análise termodinâmica do que a própria entalpia. Ele é tabulado nas tabelas de vapor, juntamente com o volume específico e a energia interna específica . A eficiência térmica desse ciclo simples de Rankine e em termos de entalpias específicas seria:
É uma equação muito simples e, para determinar a eficiência térmica, você pode usar os dados das tabelas de vapor .
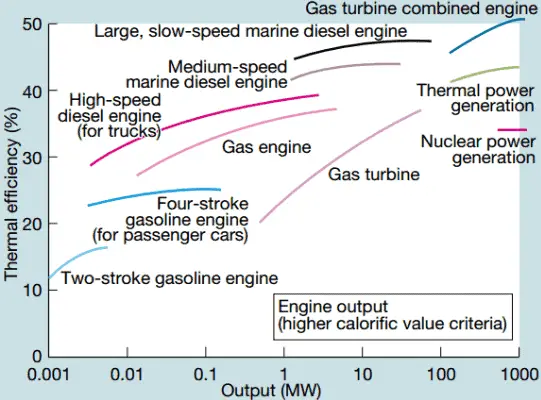
Eficiência térmica da turbina a vapor
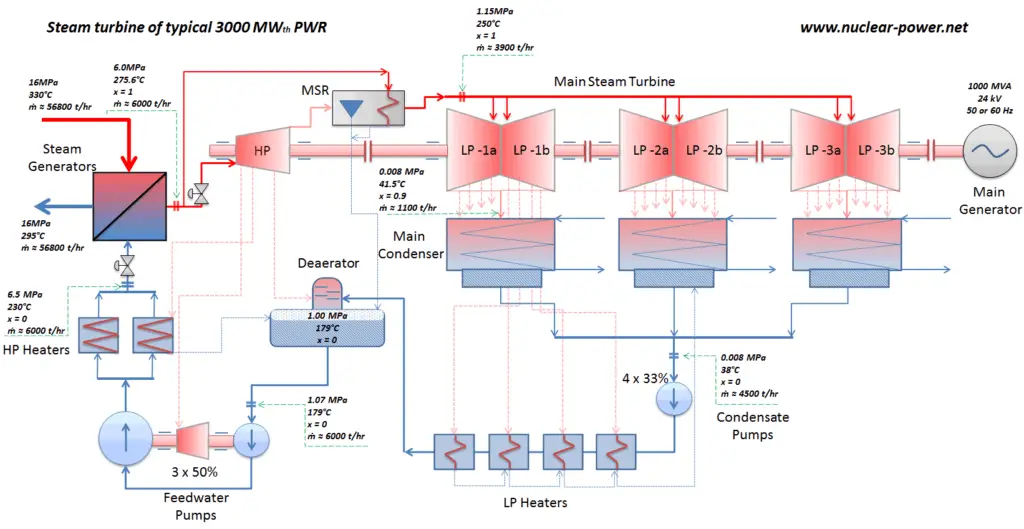
Nas modernas usinas nucleares, a eficiência térmica geral é de cerca de um terço (33%), de modo que são necessários 3000 MWth de energia térmica da reação de fissão para gerar 1000 MWe de energia elétrica. O motivo está na temperatura do vapor relativamente baixa ( 6 MPa ; 275,6 ° C). Eficiências mais altas podem ser alcançadas aumentando a temperaturado vapor. Mas isso requer um aumento nas pressões dentro de caldeiras ou geradores de vapor. No entanto, considerações metalúrgicas impõem limites superiores a essas pressões. Em comparação com outras fontes de energia, a eficiência térmica de 33% não é grande. Mas deve-se notar que as usinas nucleares são muito mais complexas que as usinas de combustíveis fósseis e é muito mais fácil queimar combustíveis fósseis do que gerar energia a partir de combustíveis nucleares. As usinas subcríticas de combustíveis fósseis, que são operadas sob pressão crítica (ou seja, inferiores a 22,1 MPa), podem atingir uma eficiência de 36 a 40%.
Causas de ineficiência
Como foi discutido, uma eficiência pode variar entre 0 e 1. Cada mecanismo térmico é de alguma forma ineficiente. Essa ineficiência pode ser atribuída a três causas.
- Irreversibilidade de processos . Existe um limite superior teórico geral para a eficiência da conversão de calor em trabalho em qualquer motor térmico. Esse limite superior é chamado de eficiência de Carnot . De acordo com o princípio Carnot , nenhum motor pode ser mais eficiente que um motor reversível ( um motor térmico Carnot ) operando entre os mesmos reservatórios de alta e baixa temperatura. Por exemplo, quando o reservatório quente tem T quente de 400 ° C (673K) e T frio de cerca de 20 ° C (293K), a eficiência máxima (ideal) será: = 1 – T frio / T quente = 1 – 293 / 673 = 56%. Mas todos os processos termodinâmicos reais são de alguma forma irreversíveis. Eles não são feitos infinitamente devagar. Portanto, os motores térmicos devem ter eficiências mais baixas do que os limites de eficiência devido à irreversibilidade inerente ao ciclo dos motores térmicos que utilizam.
- Presença de fricção e perdas de calor. Em sistemas termodinâmicos reais ou em motores térmicos reais, parte da ineficiência geral do ciclo é devida às perdas dos componentes individuais. Em dispositivos reais (como turbinas, bombas e compressores), um atrito mecânico , perdas de calor e perdas no processo de combustão causam mais perdas de eficiência.
- Ineficiência do projeto . Finalmente, a última e também importante fonte de ineficiências provém dos compromissos assumidos pelos engenheiros ao projetar um motor térmico (por exemplo, usina). Eles devem considerar o custo e outros fatores no design e operação do ciclo. Como exemplo, considere um projeto do condensador nas usinas termelétricas. Idealmente, o vapor descarregado no condensador não teria sub-resfriamento . Mas os condensadores reais são projetados para sub-resfriar o líquido em alguns graus Celsius, a fim de evitar a cavitação de sucção nas bombas de condensado. Porém, esse sub-resfriamento aumenta a ineficiência do ciclo, porque é necessária mais energia para reaquecer a água.
Melhoria da eficiência térmica – Turbina a vapor
Existem vários métodos, como pode ser melhorada a eficiência térmica do ciclo Rankine. Assumindo que a temperatura máxima seja limitada pela pressão dentro do vaso de pressão do reator, esses métodos são:
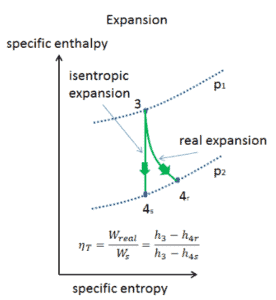
Eficiência isentrópica – turbina, bomba
Nos capítulos anteriores assumiu-se que a expansão do vapor é isentrópica e, portanto, utilizou-se o t 4, é como a temperatura de saída do gás. Essas premissas são aplicáveis apenas aos ciclos ideais.
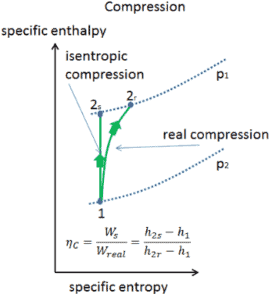
A maioria dos dispositivos de fluxo constante (turbinas, compressores, bicos) opera em condições adiabáticas, mas não são verdadeiramente isentrópicos, mas são idealizados como isentrópicos para fins de cálculo. Definimos os parâmetros η T , η P , η N , como uma razão entre o trabalho real realizado pelo dispositivo e o trabalho por dispositivo quando operado em condições isentrópicas (no caso de turbinas). Essa relação é conhecida como Eficiência de turbina isentrópica / bomba / bico . Esses parâmetros descrevem com que eficiência uma turbina, compressor ou bico se aproxima de um dispositivo isentrópico correspondente. Este parâmetro reduz a eficiência geral e a produção do trabalho. Para turbinas, o valor de η T é tipicamente de 0,7 a 0,9 (70-90%).
Veja também: Processo isentrópico
Turbina a Vapor – Problema com a Solução
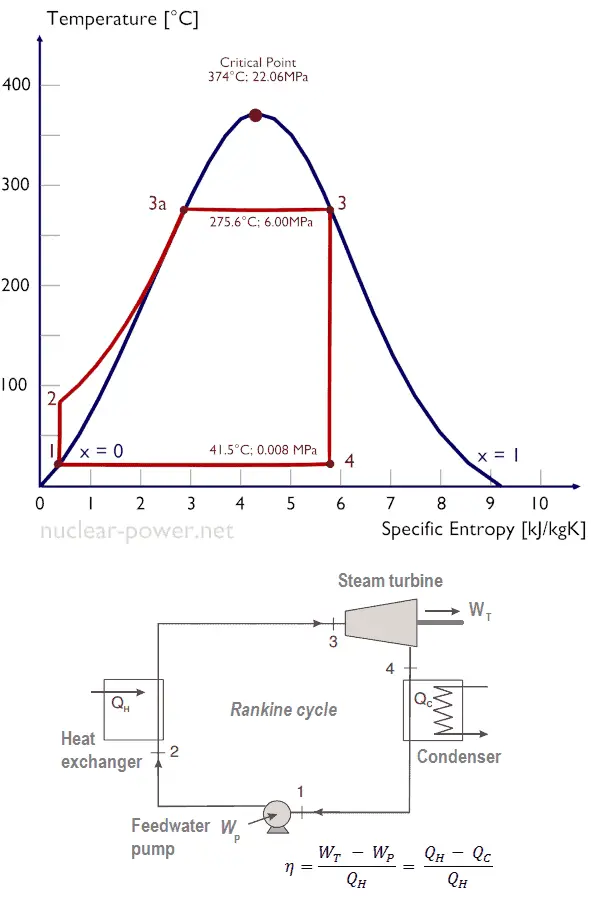 Vamos assumir o ciclo Rankine , que é um dos ciclos termodinâmicos mais comuns em usinas termelétricas. Nesse caso, assuma um ciclo simples, sem reaquecimento e sem a turbina a vapor de condensação funcionando com vapor saturado (vapor seco). Nesse caso, a turbina opera em estado estacionário com condições de entrada de 6 MPa, t = 275,6 ° C, x = 1 (ponto 3). O vapor sai deste estágio da turbina a uma pressão de 0,008 MPa, 41,5 ° C e x = ??? (ponto 4)
Vamos assumir o ciclo Rankine , que é um dos ciclos termodinâmicos mais comuns em usinas termelétricas. Nesse caso, assuma um ciclo simples, sem reaquecimento e sem a turbina a vapor de condensação funcionando com vapor saturado (vapor seco). Nesse caso, a turbina opera em estado estacionário com condições de entrada de 6 MPa, t = 275,6 ° C, x = 1 (ponto 3). O vapor sai deste estágio da turbina a uma pressão de 0,008 MPa, 41,5 ° C e x = ??? (ponto 4)
Calcular:
- a qualidade do vapor do vapor de saída
- a diferença de entalpia entre estes dois estados (3 → 4), a qual corresponde ao trabalho realizado pelo vapor, W t .
- a diferença de entalpia entre estes dois estados (1 → 2), que corresponde ao trabalho feito por bombas, W P .
- a diferença de entalpia entre esses dois estados (2 → 3), que corresponde ao calor líquido adicionado no gerador de vapor
- a eficiência termodinâmica deste ciclo e compare esse valor com a eficiência de Carnot
1)
Como não sabemos a qualidade exata do vapor de saída, precisamos determinar esse parâmetro. O estado 4 é fixado pela pressão p 4 = 0,008 MPa e o fato de que a entropia específica é constante para a expansão isentrópica (s 3 = s 4 = 5,89 kJ / kgK para 6 MPa ). A entropia específica da água líquida saturada (x = 0) e do vapor seco (x = 1) pode ser selecionada nas tabelas de vapor . No caso de vapor úmido, a entropia real pode ser calculada com a qualidade do vapor, x, e as entropias específicas de água líquida saturada e vapor seco:
s 4 = s v x + (1 – x) s l
Onde
s 4 = entropia de vapor úmido (J / kg K) = 5,89 kJ / kgK
s v = entropia do vapor “seco” (J / kg K) = 8,227 kJ / kgK (para 0,008 MPa)
s l = entropia de água líquida saturada (J / kg K) = 0,592 kJ / kgK (para 0,008 MPa)
A partir desta equação, a qualidade do vapor é:
x 4 = ( s 4 – s l ) / ( s v – s l ) = (5,89 – 0,592) / (8,227 – 0,592) = 0,694 = 69,4%
2)
A entalpia para o estado 3 pode ser coletada diretamente das tabelas de vapor, enquanto a entalpia para o estado 4 deve ser calculada usando a qualidade do vapor:
h 3, v = 2785 kJ / kg
h 4, molhado = h 4, v x + (1 – x) h 4, l = 2576. 0,694 + (1 – 0,694). 174 = 1787 + 53,2 = 1840 kJ / kg
Então o trabalho realizado pelo vapor, W T, é
W T = Δh = 945 kJ / kg
3)
A entalpia para o estado 1 pode ser obtida diretamente das tabelas de vapor:
h 1, l = 174 kJ / kg
O estado 2 é fixado pela pressão p 2 = 6,0 MPa e pelo fato de a entropia específica ser constante para a compressão isentrópica (s 1 = s 2 = 0,592 kJ / kgK para 0,008 MPa ). Para esta entropia s 2 = 0,592 kJ / kgK ep 2 = 6,0 MPa, encontramos h 2, sub-resfriado em tabelas de vapor para água comprimida (usando interpolação entre dois estados).
h 2, sub-resfriado = 179,7 kJ / kg
Então, o trabalho realizado pelas bombas, W P, é
W P = Δh = 5,7 kJ / kg
4)
A diferença de entalpia entre (2 → 3), que corresponde ao calor líquido adicionado no gerador de vapor, é simplesmente:
Q add = h 3, v – h 2, sub-resfriado = 2785 – 179,7 = 2605,3 kJ / kg
Observe que, não há regeneração de calor neste ciclo. Por outro lado, a maior parte do calor adicionado é para a entalpia da vaporização (isto é, para a mudança de fase).
5)
Nesse caso, geradores de vapor, turbinas a vapor, condensadores e bombas de água de alimentação constituem um motor térmico, sujeito às limitações de eficiência impostas pela segunda lei da termodinâmica . No caso ideal (sem atrito, processos reversíveis, design perfeito), este motor térmico teria uma eficiência de Carnot de
η Carnot = 1 – T frio / T quente = 1 – 315/549 = 42,6%
onde a temperatura do reservatório quente é de 275,6 ° C (548,7 K), a temperatura do reservatório frio é de 41,5 ° C (314,7 K).
A eficiência termodinâmica deste ciclo pode ser calculada pela seguinte fórmula:
assim
η th = (945 – 5,7) / 2605,3 = 0,361 = 36,1%
……………………………………………………………………………………………………………………………….
Este artigo é baseado na tradução automática do artigo original em inglês. Para mais informações, consulte o artigo em inglês. Você pode nos ajudar. Se você deseja corrigir a tradução, envie-a para: translations@nuclear-power.com ou preencha o formulário de tradução on-line. Agradecemos sua ajuda, atualizaremos a tradução o mais rápido possível. Obrigado.