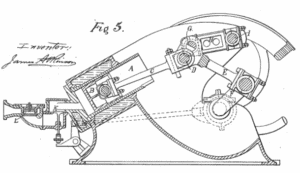
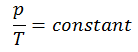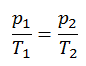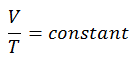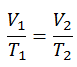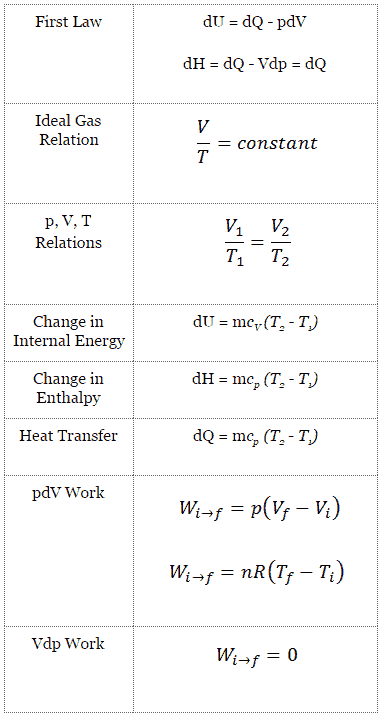Facebook Instagram Youtube Twitter

What is Atkinson Cycle – Processes – Definition

by
In an Atkinson cycle (modified Otto cycle), there is a series of four processes: two isentropic processes alternated with anisochoric process and an isobaric process. Thermal Engineering

Atkinson Cycle – Processes

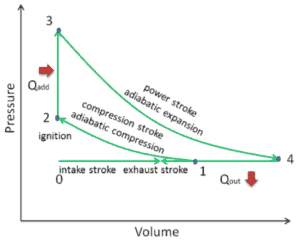
In an Atkinson cycle (modified Otto cycle), the system executing the cycle undergoes a series of four processes: two isentropic (reversible adiabatic) processes alternated with one isochoric process and one isobaric process:

  • Isentropic compression (compression stroke) – The gas (fuel-air mixture) is compressed adiabatically from state 1 to state 2, as the piston moves from intake valve closing point (1) to top dead center. The surroundings do work on the gas, increasing its internal energy (temperature) and compressing it. On the other hand the entropy remains unchanged. The changes in volumes and its ratio (V1 / V2) is known as the compression ratio. The compression ratio is smaller than the expansion ratio.
  • Isochoric compression (ignition phase) – In this phase (between state 2 and state 3) there is a constant-volume (the piston is at rest ) heat transfer to the air from an external source while the piston is at rest at top dead center. This process is similar to the isochoric process in the Otto cycle. It is intended to represent the ignition of the fuel–air mixture injected into the chamber and the subsequent rapid burning. The pressure rises and the ratio (P3 / P2) is known as the “explosion ratio”.
  • Isentropic expansion (power stroke) – The gas expands adiabatically from state 3 to state 4, as the piston moves from top dead center to bottom dead center. The gas does work on the surroundings (piston) and loses an amount of internal energy equal to the work that leaves the system. Again the entropy remains unchanged. The volume ratio (V4 / V3) is known as the isentropic expansion ratio.
  • Isobaric exhaust (exhaust stroke) – The main goal of the modern Atkinson cycle is to allow the pressure in the combustion chamber at the end of the power stroke to be equal to atmospheric pressure. Since there can be atmospheric pressure in the chamber, then there is no decompression as in an Otto cycle. The piston moves from bottom dead center (BDC) to top dead center (TDC) and the cycle passes points 4 → 1 → 0. In this stroke the exhaust valve is open while the piston pulls an exhaust gases out of the chamber.

During the Atkinson cycle, work is done on the gas by the piston between states 1 and 2 (isentropic compression). Work is done by the gas on the piston between stages 3 and 4 (isentropic expansion). The difference between the work done by the gas and the work done on the gas is the net work produced by the cycle and it corresponds to the area enclosed by the cycle curve. The work produced by the cycle times the rate of the cycle (cycles per second) is equal to the power produced by the Atkinson engine.

Atkinson gas engine
Atkinson gas engine as shown in US Patent 367496
Atkinson Cycle - pV diagram
Atkinson Cycle – pV diagram

Isentropic Process

An isentropic process is a thermodynamic process, in which the entropy of the fluid or gas remains constant. It means the isentropic process is a special case of an adiabatic process in which there is no transfer of heat or matter. It is a reversible adiabatic process. The assumption of no heat transfer is very important, since we can use the adiabatic approximation only in very rapid processes.

Isentropic Process and the First Law

For a closed system, we can write the first law of thermodynamics in terms of enthalpy:

dH = dQ + Vdp

or

dH = TdS + Vdp

Isentropic process (dQ = 0):

dH = Vdp     →     W = H2 – H1     →     H2 – H1 = Cp (T2 – T1)    (for ideal gas)

Isentropic Process of the Ideal Gas

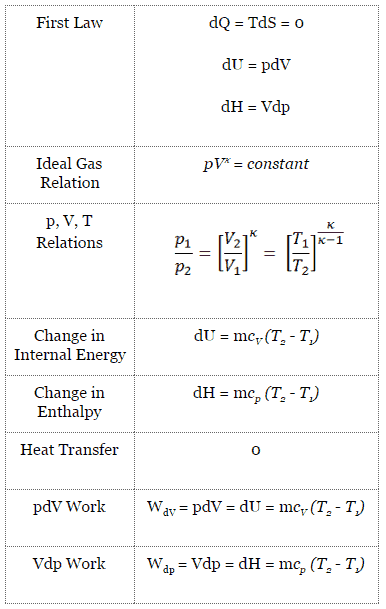
The isentropic process (a special case of adiabatic process) can be expressed with the ideal gas law as:

pVκ = constant

or

p1V1κ = p2V2κ

in which κ = cp/cv is the ratio of the specific heats (or heat capacities) for the gas. One for constant pressure (cp) and one for constant volume (cv). Note that, this ratio κ  = cp/cv is a factor in determining the speed of sound in a gas and other adiabatic processes.

Isochoric Process

An isochoric process is a thermodynamic process, in which the volume of the closed system remains constant (V = const). It describes the behavior of gas inside the container, that cannot be deformed. Since the volume remains constant, the heat transfer into or out of the system does not the p∆V work, but only changes the internal energy (the temperature) of the system.

Isochoric Process and the First Law

The classical form of the first law of thermodynamics is the following equation:

dU = dQ – dW

In this equation dW is equal to dW = pdV and is known as the boundary work. Then:

dU = dQ  – pdV

In isochoric process and the ideal gas, all of heat added to the system will be used to increase the internal energy.

Isochoric process (pdV = 0):

dU = dQ    (for ideal gas)

dU = 0 = Q – W    →     W = Q      (for ideal gas)

Isochoric Process of the Ideal Gas

The isochoric process can be expressed with the ideal gas law as:

isochoric process - equation 1

or

isochoric process - equation 2

On a p-V diagram, the process occurs along a horizontal line that has the equation V = constant.

See also: Guy-Lussac’s Law

Isobaric Process

An isobaric process is a thermodynamic process, in which the pressure of the system remains constant (p = const). The heat transfer into or out of the system does work, but also changes the internal energy of the system.

Since there are changes in internal energy (dU) and changes in system volume (∆V), engineers often use the enthalpy of the system, which is defined as:

H = U + pV

Isobaric Process and the First Law

The classical form of the first law of thermodynamics is the following equation:

dU = dQ – dW

In this equation dW is equal to dW = pdV and is known as the boundary work. In an isobaric process and the ideal gas, part of heat added to the system will be used to do work and part of heat added will increase the internal energy (increase the temperature). Therefore it is convenient to use the enthalpy instead of the internal energy.

Isobaric process (Vdp = 0):

dH = dQ → Q = H2 – H1

At constant entropy, i.e. in isentropic process, the enthalpy change equals the flow process work done on or by the system.

Isobaric Process of the Ideal Gas

The isobaric process can be expressed with the ideal gas law as:

isobaric process - equation - 2

or

isobaric process - equation - 3

On a p-V diagram, the process occurs along a horizontal line (called an isobar) that has the equation p = constant.

See also: Charles’s Law

Isentropic Process - characteristics
Isentropic process – main characteristics
Isochoric process - main characteristics
Isochoric process – main characteristics
Isobaric process - main characteristics
Isobaric process – main characteristics
 
References:
Nuclear and Reactor Physics:
  1. J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
  2. J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
  3. W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
  4. Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
  5. W.S.C. Williams. Nuclear and Particle Physics. Clarendon Press; 1 edition, 1991, ISBN: 978-0198520467
  6. Kenneth S. Krane. Introductory Nuclear Physics, 3rd Edition, Wiley, 1987, ISBN: 978-0471805533
  7. G.R.Keepin. Physics of Nuclear Kinetics. Addison-Wesley Pub. Co; 1st edition, 1965
  8. Robert Reed Burn, Introduction to Nuclear Reactor Operation, 1988.
  9. U.S. Department of Energy, Nuclear Physics and Reactor Theory. DOE Fundamentals Handbook, Volume 1 and 2. January 1993.

Advanced Reactor Physics:

  1. K. O. Ott, W. A. Bezella, Introductory Nuclear Reactor Statics, American Nuclear Society, Revised edition (1989), 1989, ISBN: 0-894-48033-2.
  2. K. O. Ott, R. J. Neuhold, Introductory Nuclear Reactor Dynamics, American Nuclear Society, 1985, ISBN: 0-894-48029-4.
  3. D. L. Hetrick, Dynamics of Nuclear Reactors, American Nuclear Society, 1993, ISBN: 0-894-48453-2.
  4. E. E. Lewis, W. F. Miller, Computational Methods of Neutron Transport, American Nuclear Society, 1993, ISBN: 0-894-48452-4.

See also:

Atkinson Cycle

We hope, this article, Atkinson Cycle – Processes, helps you. If so, give us a like in the sidebar. Main purpose of this website is to help the public to learn some interesting and important information about thermal engineering.

Related Posts