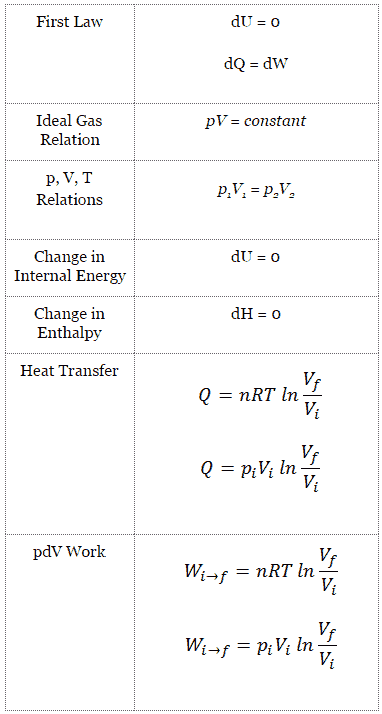What is Carnot Cycle – Types of Processes – Definition

Carnot Cycle – Processes

In a Carnot cycle, the system executing the cycle undergoes a series of four internally reversible processes: two isentropic processes (reversible adiabatic) alternated with two isothermal processes:

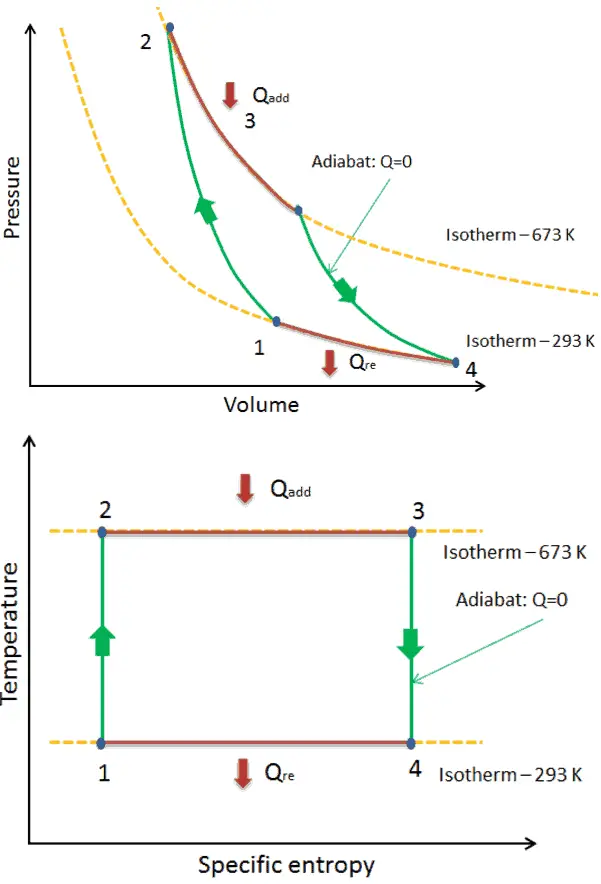
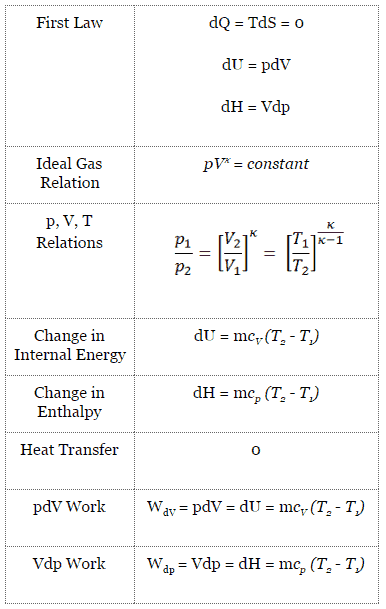
1. isentropic compression – The gas is compressed adiabatically from state 1 to state 2, where the temperature is T_H. The surroundings do work on the gas, increasing its internal energy and compressing it. On the other hand the entropy remains unchanged.
2. Isothermal  expansion – The system is placed in contact with the reservoir at T_H. The gas expands isothermally while receiving energy Q_H from the hot reservoir by heat transfer. The temperature of the gas does not change during the process. The gas does work on the surroundings. The total entropy change is given by: ∆S = S₁ – S₄ = Q_H/T_H
3. isentropic expansion – The gas expands adiabatically from state 3 to state 4, where the temperature is T_C. The gas does work on the surroundings and loses an amount of internal energy equal to the work that leaves the system. Again the entropy remains unchanged.
4. isothermal compression – The system is placed in contact with the reservoir at T_C. The gas compresses isothermally to its initial state while it discharges energy Q_C to the cold reservoir by heat transfer. In this process the surroundings do work on the gas. The total entropy change is given by: ∆S = S₃ – S₂ = Q_C/T_C

Isentropic Process

An isentropic process is a thermodynamic process, in which the entropy of the fluid or gas remains constant. It means the isentropic process is a special case of an adiabatic process in which there is no transfer of heat or matter. It is a reversible adiabatic process. The assumption of no heat transfer is very important, since we can use the adiabatic approximation only in very rapid processes.

Isentropic Process and the First Law

For a closed system, we can write the first law of thermodynamics in terms of enthalpy:

dH = dQ + Vdp

or

dH = TdS + Vdp

Isentropic process (dQ = 0):

dH = Vdp     →     W = H₂ – H₁     →     H₂ – H₁ = C_p (T₂ – T₁)    (for ideal gas)

Isentropic Process of the Ideal Gas

The isentropic process (a special case of adiabatic process) can be expressed with the ideal gas law as:

pV^κ = constant

or

p₁V₁^κ = p₂V₂^κ

in which κ = c_p/c_v is the ratio of the specific heats (or heat capacities) for the gas. One for constant pressure (c_p) and one for constant volume (c_v). Note that, this ratio κ  = c_p/c_v is a factor in determining the speed of sound in a gas and other adiabatic processes.

Isothermal Process

An isothermal process is a thermodynamic process, in which the temperature of the system remains constant (T = const). The heat transfer into or out of the system typically must happen at such a slow rate in order to continually adjust to the temperature of the reservoir through heat exchange. In each of these states the thermal equilibrium is maintained.

Isothermal Process and the First Law

The classical form of the first law of thermodynamics is the following equation:

dU = dQ – dW

In this equation dW is equal to dW = pdV and is known as the boundary work.

In isothermal process and the ideal gas, all heat added to the system will be used to do work:

Isothermal process (dU = 0):

dU = 0 = Q – W    →     W = Q      (for ideal gas)

Isothermal Process of the Ideal Gas

The isothermal process can be expressed with the ideal gas law as:

pV = constant

or

p₁V₁ = p₂V₂

On a p-V diagram, the process occurs along a line (called an isotherm) that has the equation p = constant / V.

See also: Boyle-Mariotte Law

See also:

Carnot Cycle