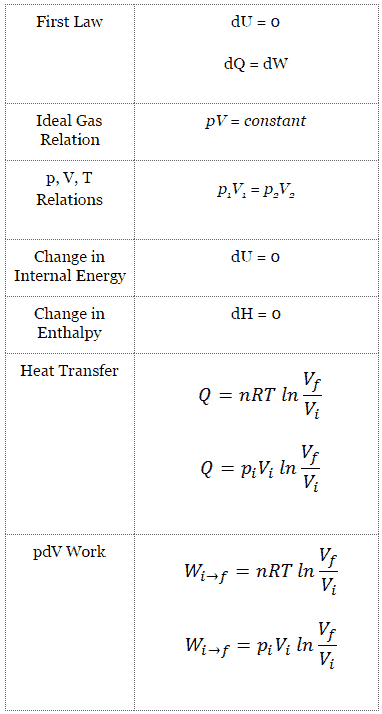Ciclo de Carnot – Processos
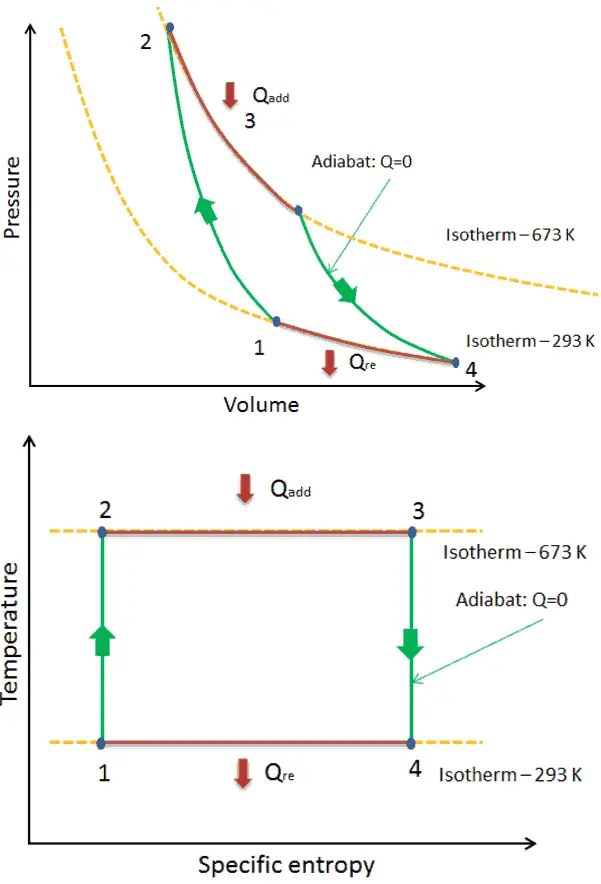Em um ciclo de Carnot , o sistema que executa o ciclo passa por uma série de quatro processos reversíveis internamente : dois processos isentrópicos (adiabáticos reversíveis) alternados com dois processos isotérmicos :
- compressão isentrópica – O gás é comprimido adiabaticamente a partir de um estado para o estado 2, onde a temperatura é T H . Os arredores trabalham com o gás, aumentando sua energia interna e comprimindo-a. Por outro lado, a entropia permanece inalterada .
- Expansão isotérmica – O sistema é colocado em contacto com o reservatório em T H . O gás se expande isotérmica enquanto recebe energia Q H do reservatório quente por transferência de calor. A temperatura do gás não muda durante o processo. O gás funciona nos arredores. A variação total da entropia é dada por: ∆S = S 1 – S 4 = Q H / T H
- expansão isentrópica – O gás expande-se adiabaticamente de estado 3 para o estado 4, onde a temperatura é T C . O gás trabalha nos arredores e perde uma quantidade de energia interna igual ao trabalho que sai do sistema. Novamente a entropia permanece inalterada.
- compressão isotérmica – O sistema é colocado em contacto com o reservatório em T C . O gás é comprimido isotérmica ao seu estado inicial enquanto descarrega energia Q C para o reservatório frio por transferência de calor. Nesse processo, o ambiente trabalha com o gás. A variação total da entropia é dada por: ∆S = S 3 – S 2 = Q C / T C
Processo isentrópico
Um processo isentrópico é um processo termodinâmico , no qual a entropia do fluido ou gás permanece constante. Isso significa que o processo isentrópico é um caso especial de um processo adiabático no qual não há transferência de calor ou matéria. É um processo adiabático reversível . A suposição de que não há transferência de calor é muito importante, pois podemos usar a aproximação adiabática apenas em processos muito rápidos .
Processo isentrópico e a primeira lei
Para um sistema fechado, podemos escrever a primeira lei da termodinâmica em termos de entalpia :
dH = dQ + Vdp
ou
dH = TdS + Vdp
Processo isentrópico (dQ = 0):
dH = Vdp → W = H 2 – H 1 → H 2 – H 1 = C P (T 2 – T 1 ) (para gás ideal )
Processo isentrópico do gás ideal
O processo isentrópico (um caso especial de processo adiabático) pode ser expresso com a lei dos gases ideais como:
pV κ = constante
ou
p 1 V 1 k = p 2 V 2 k
em que κ = c p / c v é a proporção de aquecimentos específicos (ou capacidades de calor ) para o gás. Um para pressão constante (c p ) e outro para volume constante (c v ) . Observe que essa razão κ = c p / c v é um fator na determinação da velocidade do som em um gás e em outros processos adiabáticos.
Processo isotérmico
Um processo isotérmico é um processo termodinâmico , no qual a temperatura do sistema permanece constante (T = const). A transferência de calor para dentro ou para fora do sistema geralmente deve ocorrer a uma taxa tão lenta, a fim de se ajustar continuamente à temperatura do reservatório através da troca de calor. Em cada um desses estados, o equilíbrio térmico é mantido.
Processo isotérmico e a primeira lei
A forma clássica da primeira lei da termodinâmica é a seguinte equação:
dU = dQ – dW
Nesta equação, dW é igual a dW = pdV e é conhecido como trabalho de fronteira .
No processo isotérmico e no gás ideal , todo o calor adicionado ao sistema será usado para realizar o trabalho:
Processo isotérmico (dU = 0):
dU = 0 = Q – W → W = Q (para gás ideal)
Processo isotérmico do gás ideal
O processo isotérmico pode ser expresso com a lei do gás ideal como:
pV = constante
ou
p 1 V 1 = p 2 V 2
Em um diagrama pV, o processo ocorre ao longo de uma linha (chamada uma isotérmica) que tem a equação p = constante / V .
Veja também: Lei de Boyle-Mariotte
……………………………………………………………………………………………………………………………….
Este artigo é baseado na tradução automática do artigo original em inglês. Para mais informações, consulte o artigo em inglês. Você pode nos ajudar. Se você deseja corrigir a tradução, envie-a para: translations@nuclear-power.com ou preencha o formulário de tradução on-line. Agradecemos sua ajuda, atualizaremos a tradução o mais rápido possível. Obrigado.
