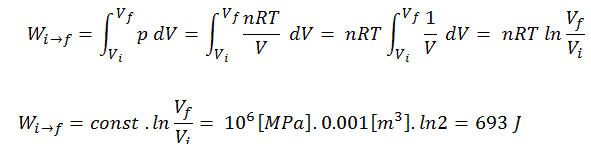Processus isotherme
Un processus isotherme est un processus thermodynamique , dans lequel la température du système reste constante (T = const). Le transfert de chaleur dans ou hors du système doit généralement se produire à un rythme aussi lent afin de s’adapter en permanence à la température du réservoir par échange de chaleur. Dans chacun de ces états, l’ équilibre thermique est maintenu.
Pour un gaz parfaitet un procédé polytropique, le cas n = 1 correspond à un procédé isotherme (à température constante). Contrairement au processus adiabatique , dans lequel n = κ et un système n’échange pas de chaleur avec son environnement (Q = 0; ∆T ≠ 0 ) , dans un processus isotherme, il n’y a pas de changement dans l’énergie interne (due à ∆T = 0 ) et donc ΔU = 0 (pour les gaz idéaux) et Q ≠ 0. Un processus adiabatique n’est pas nécessairement un processus isotherme, ni un processus isotherme nécessairement adiabatique.
En ingénierie, les changements de phase, tels que l’évaporation ou la fusion, sont des processus isothermes lorsque, comme c’est généralement le cas, ils se produisent à pression et température constantes.
Processus isotherme et première loi
La forme classique de la première loi de la thermodynamique est l’équation suivante:
dU = dQ – dW
Dans cette équation, dW est égal à dW = pdV et est connu comme le travail aux limites .
Dans le processus isotherme et le gaz parfait , toute la chaleur ajoutée au système sera utilisée pour effectuer les travaux:
Processus isotherme (dU = 0):
dU = 0 = Q – W → W = Q (pour le gaz parfait)
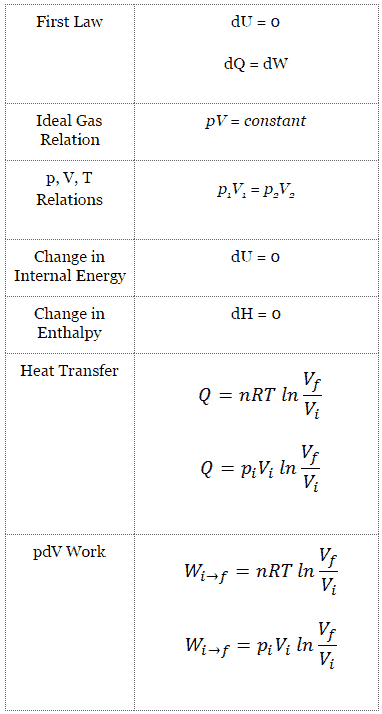
Expansion isotherme – Compression isotherme
Voir aussi: Qu’est-ce qu’un gaz parfait
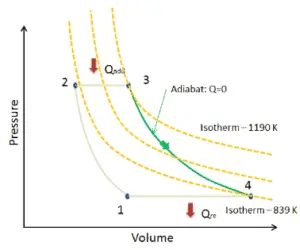Dans un gaz parfait , les molécules n’ont pas de volume et n’interagissent pas. Selon la loi du gaz parfait , la pression varie linéairement avec la température et la quantité, et inversement avec le volume .
pV = nRT
où:
- p est la pression absolue du gaz
- n est la quantité de substance
- T est la température absolue
- V est le volume
- R est la constante de gaz parfaite ou universelle, égale au produit de la constante de Boltzmann et de la constante d’Avogadro,
Dans cette équation, le symbole R est une constante appelée constante de gaz universelle qui a la même valeur pour tous les gaz, à savoir R = 8,31 J / mol K.
Le processus isotherme peut s’exprimer avec la loi du gaz parfait comme:
pV = constant
ou
p 1 V 1 = p 2 V 2
Sur un diagramme pV, le processus se produit le long d’ une ligne (appelée isotherme) qui a l’équation p = constante / V .
Loi Boyle – Mariotte
La loi de Boyle-Mariotte est l’une des lois sur le gaz . À la fin du XVIIe siècle, Robert William Boyle et Edme Mariotte ont étudié indépendamment la relation entre le volume et la pression d’un gaz à température constante . Les résultats de certaines expériences avec des gaz à relativement basse pression ont conduit Robert Boyle à formuler une loi bien connue. Il déclare que:
Pour une masse fixe de gaz à température constante, le volume est inversement proportionnel à la pression.
Cela signifie que, par exemple, si vous augmentez le volume 10 fois, la pression diminuera 10 fois. Si vous divisez par deux le volume, vous doublerez la pression.
Vous pouvez exprimer cela mathématiquement comme:
pV = constant
ou
p 1 V 1 = p 2 V 2
Oui, il semble être identique au processus isotherme du gaz parfait. En fait, pendant leurs expériences, la température reste constante comme l’avait supposé Mariotte. Ces résultats sont parfaitement cohérents avec la loi du gaz parfait , qui détermine que la constante est égale à nRT .
pV = nRT
où:
- p est la pression absolue du gaz
- n est la quantité de substance
- T est la température absolue
- V est le volume
- R est la constante de gaz parfaite ou universelle, égale au produit de la constante de Boltzmann et de la constante d’Avogadro,
Dans cette équation, le symbole R est une constante appelée constante de gaz universelle qui a la même valeur pour tous les gaz, à savoir R = 8,31 J / mol K.
Exemple de processus isotherme
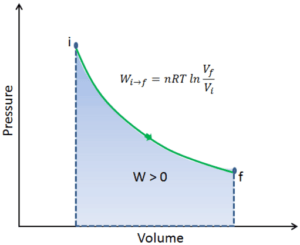
Supposons une expansion isotherme de l’hélium (i → f) dans un piston sans friction (système fermé). La détente du gaz est propulsée par absorption d’énergie thermique Q add . Le gaz se détend à partir d’un volume initial de 0,001 m3 et simultanément la charge externe du piston diminue lentement et en continu de 1 MPa à 0,5 MPa. L’hélium se comportant presque comme un gaz parfait, utilisez la loi du gaz parfait pour calculer le volume final de la chambre, puis calculez le travail effectué par le système, lorsque la température du gaz est égale à 400 K.
Solution:
Le volume final du gaz, V f , peut être calculé en utilisant la relation p, V, T pour le processus isotherme:
p i V i = p f V f ⇒ V f = p i V i / p f = 2 x 0,001 m 3 = 0,002 m 3
Pour calculer de tels processus, nous aurions besoin de savoir comment la pression varie avec le volume pour le processus réel par lequel le système passe de l’état i à l’état f . Étant donné que pendant ce processus, la pression interne n’était pas constante, le travail p∆V effectué par le piston doit être calculé en utilisant l’intégrale suivante:
Par convention, une valeur positive pour le travail indique que le travail est effectué par le système sur son environnement. Une valeur négative indique que le travail est effectué sur le système par son environnement. Le travail pΔV est égal à l’aire sous la courbe de processus tracée sur le diagramme pression-volume.
Expansion gratuite – Expansion Joule
Ce sont des processus adiabatiques dans lesquels aucun transfert de chaleur ne se produit entre le système et son environnement et aucun travail n’est effectué sur ou par le système. Ces types de processus adiabatiques sont appelés expansion libre . Il s’agit d’un processus irréversible dans lequel un gaz se détend dans une chambre sous vide isolée. Il est également appelé expansion Joule . Pour un gaz parfait, la température ne change pas (cela signifie que le processus est également isotherme ) , cependant, les vrais gaz subissent un changement de température pendant la détente libre. En expansion libre Q = W = 0, et le première principe exige que:
dE int = 0
Une expansion libre ne peut pas être tracée sur un diagramme PV, car le processus est rapide et non quasi statique. Les états intermédiaires ne sont pas des états d’équilibre, et donc la pression n’est pas clairement définie.
……………………………………………………………………………………………………………………………….
Cet article est basé sur la traduction automatique de l’article original en anglais. Pour plus d’informations, voir l’article en anglais. Pouvez vous nous aider Si vous souhaitez corriger la traduction, envoyez-la à l’adresse: translations@nuclear-power.com ou remplissez le formulaire de traduction en ligne. Nous apprécions votre aide, nous mettrons à jour la traduction le plus rapidement possible. Merci
