What is Rankine Cycle – Processes – Expansion and Compression – Definition

Rankine Cycle – Processes

In an ideal Rankine cycle, the system executing the cycle undergoes a series of four processes: two isentropic (reversible adiabatic) processes alternated with two isobaric processes.

Rankine Cycle – Processes

• 

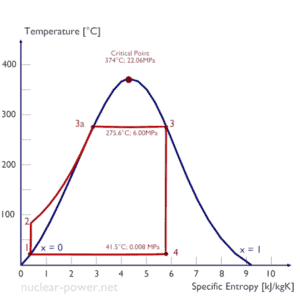
  Isentropic compression (compression in centrifugal pumps) – The liquid condensate is compressed adiabatically from state 1 to state 2 by centrifugal pumps (usually by condensate pumps and then by feedwater pumps). The liquid condensatei s pumped from the condenser into the higher pressure boiler. In this process, the surroundings do work on the fluid, increasing its enthalpy (h = u+pv) and compressing it (increasing its pressure). On the other hand the entropy remains unchanged. The work required for the compressor is given by W_Pumps = H₂ – H₁.

• Isobaric heat addition (in a heat exchanger – boiler) – In this phase (between state 2 and state 3) there is a constant-pressure heat transfer to the liquid condensate from an external source, since the chamber is open to flow in and out.  The feedwater (secondary circuit) is heated from to the boiling point (2 → 3a) of that fluid and then evaporated in the boiler (3a → 3). The net heat added is given by Q_add = H₃ – H₂
• Isentropic expansion (expansion in a steam turbine) – Steam from the boiler expands adiabatically from state 3 to state 4 in a steam turbine to produce work and then is discharged to the condenser (partially condensed). The steam does work on the surroundings (blades of the turbine) and loses an amount of enthalpy equal to the work that leaves the system. The work done by turbine is given by W_T = H₄ – H₃. Again the entropy remains unchanged.
• Isobaric heat rejection (in a heat exchanger) – In this phase the cycle completes by a constant-pressure process in which heat is rejected from the partially condensed steam. There is heat transfer from the vapor to cooling water flowing in a cooling circuit. The vapor condenses and the temperature of the cooling water increases. The net heat rejected is given by Q_re = H₄ – H₁

During a Rankine cycle, work is done on the fluid by the pumps between states 1 and 2 (isentropic compression). Work is done by the fluid in the turbine between stages 3 and 4 (isentropic expansion). The difference between the work done by the fluid and the work done on the fluid is the net work produced by the cycle and it corresponds to the area enclosed by the cycle curve (in pV diagram). The working fluid in a Rankine cycle follows a closed loop and is reused constantly.

As can be seen, it is convenient to use enthalpy and the first law in terms of enthalpy in analysis of this thermodynamic cycle. This form of the law simplifies the description of energy transfer. At constant pressure, the enthalpy change equals the energy transferred from the environment through heating:

Isobaric process (Vdp = 0):

dH = dQ     →     Q = H₂ – H₁

At constant entropy, i.e. in isentropic process, the enthalpy change equals the flow process work done on or by the system:

Isentropic process (dQ = 0):

dH = Vdp     →     W = H₂ – H₁

See also: Why power engineers use enthalpy? Answer: dH = dQ + Vdp

Isentropic Process

An isentropic process is a thermodynamic process, in which the entropy of the fluid or gas remains constant. It means the isentropic process is a special case of an adiabatic process in which there is no transfer of heat or matter. It is a reversible adiabatic process. The assumption of no heat transfer is very important, since we can use the adiabatic approximation only in very rapid processes.

Isentropic Process and the First Law

For a closed system, we can write the first law of thermodynamics in terms of enthalpy:

dH = dQ + Vdp

or

dH = TdS + Vdp

Isentropic process (dQ = 0):

dH = Vdp     →     W = H₂ – H₁    

Isobaric Process

An isobaric process is a thermodynamic process, in which the pressure of the system remains constant (p = const). The heat transfer into or out of the system does work, but also changes the internal energy of the system.

Since there are changes in internal energy (dU) and changes in system volume (∆V), engineers often use the enthalpy of the system, which is defined as:

H = U + pV

Isobaric Process and the First Law

The classical form of the first law of thermodynamics is the following equation:

dU = dQ – dW

In this equation dW is equal to dW = pdV and is known as the boundary work. In an isobaric process and the ideal gas, part of heat added to the system will be used to do work and part of heat added will increase the internal energy (increase the temperature). Therefore it is convenient to use the enthalpy instead of the internal energy.

Isobaric process (Vdp = 0):

dH = dQ → Q = H₂– H₁

At constant entropy, i.e. in isentropic process, the enthalpy change equals the flow process work done on or by the system.

Rankine Cycle – pV, Ts diagram

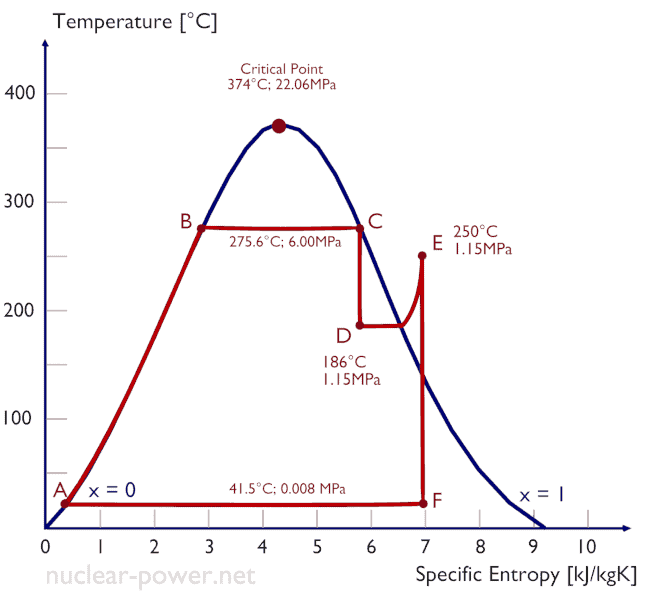
The Rankine cycle is often plotted on a pressure volume diagram (pV diagram) and on a temperature-entropy diagram (Ts diagram).

When plotted on a pressure volume diagram, the isobaric processes follow the isobaric lines for the gas (the horizontal lines), adiabatic processes move between these horizontal lines and the area bounded by the complete cycle path represents the total work that can be done during one cycle.

The temperature-entropy diagram (Ts diagram) in which the thermodynamic state is specified by a point on a graph with specific entropy (s) as the horizontal axis and absolute temperature (T) as the vertical axis. Ts diagrams are a useful and common tool, particularly because it helps to visualize the heat transfer during a process. For reversible (ideal) processes, the area under the T-s curve of a process is the heat transferred to the system during that process.

See also:

Rankine Cycle