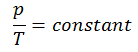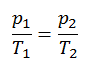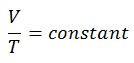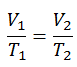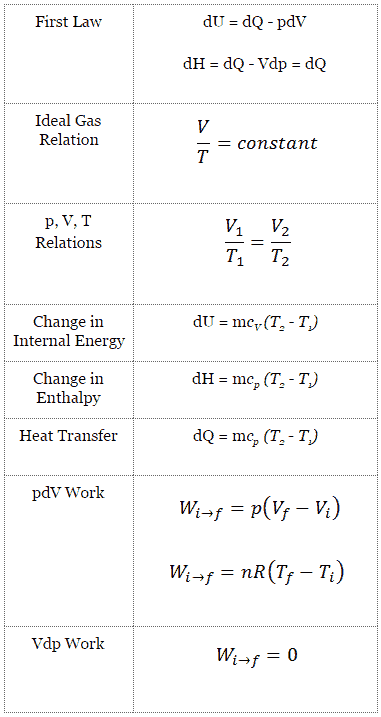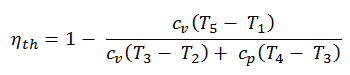Dieselzyklus – Dieselmotor
Dual-Zyklus oder begrenzter Druckzyklus ist ein thermodynamischer Zyklus , der den Otto-Zyklus und den Diesel-Zyklus kombiniert . Im Doppelzyklus erfolgt die Verbrennung teilweise bei konstantem Volumen und teilweise bei konstantem Druck. Es kann verwendet werden, um Verbrennungsmotoren zu beschreiben. Die Druck-Volumen-Diagramme der tatsächlichen Verbrennungsmotoren werden in den Zyklen Otto und Diesel nicht gut beschrieben. Ein Luftstandardzyklus, der durchgeführt werden kann, um die Druckschwankungen genauer zu approximieren, ist der Luftstandard-Doppelzyklus. Ein leistungsfähigerer Ansatz wäre die Modellierung des Verbrennungsprozesses sowohl bei Otto- als auch bei Dieselmotoren als Kombination von zwei Wärmeübertragungsprozessen, einem isochoren Prozess und einemisobarer Prozess .
Im Vergleich zu einem Otto-Zyklus, der eine sofortige Wärmezufuhr (isochore Wärmezufuhr) voraussetzt, wird in einem Doppelzyklus Wärme teilweise mit konstantem Volumen und teilweise mit konstantem Druck zugeführt . Daher besteht der Vorteil darin, dass mehr Zeit zur Verfügung steht, damit der Kraftstoff vollständig verbrennen kann. Andererseits ist die Verwendung eines Doppelzyklus etwas komplexer . Der thermische Wirkungsgrad liegt zwischen Otto- und Dieselkreislauf.
Seiliger-Kreisprozess – Prozesse
In einem Doppelzyklus durchläuft das System, das den Zyklus ausführt, eine Reihe von fünf Prozessen: zwei isentrope (reversible adiabatische) Prozesse, die sich mit zwei isochoren Prozessen und einem isobaren Prozess abwechseln:
-
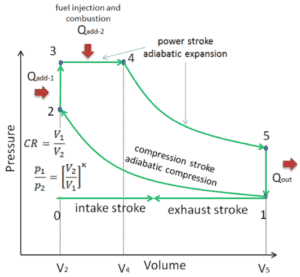
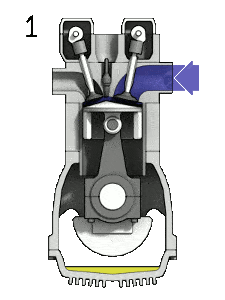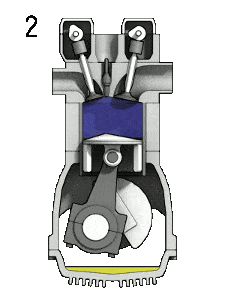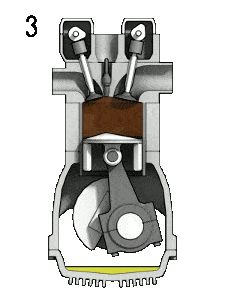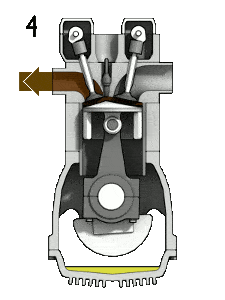
Doppelzyklus – pV-Diagramm Isentropische Kompression (Kompressionshub) – Das Gas wird adiabatisch von Zustand 1 nach Zustand 2 komprimiert, wenn sich der Kolben vom Einlassventilschließpunkt (1) zum oberen Totpunkt bewegt. Die Umgebung arbeitet am Gas, erhöht seine innere Energie (Temperatur) und komprimiert es. Andererseits bleibt die Entropie unverändert. Die Volumenänderungen und ihr Verhältnis ( V 1 / V 2 ) werden als Kompressionsverhältnis bezeichnet. Das Kompressionsverhältnis ist kleiner als das Expansionsverhältnis.
- Isochore Kompression (Zündphase) – In dieser Phase (zwischen Zustand 2 und Zustand 3) erfolgt eine Wärmeübertragung mit konstantem Volumen (der Kolben befindet sich in Ruhe) von einer externen Quelle auf die Luft, während sich der Kolben im oberen Totpunkt in Ruhe befindet . Dieser Prozess ähnelt dem isochoren Prozess im Otto-Zyklus. Es soll die Zündung des in die Kammer eingespritzten Kraftstoff-Luft-Gemisches und das anschließende schnelle Verbrennen darstellen. Der Druck steigt und das Verhältnis ( P 3 / P 2 ) wird als “Explosionsverhältnis” bezeichnet.
- Isobare Expansion (Arbeitstakt) – In dieser Phase (zwischen Zustand 3 und Zustand 4) erfolgt eine Wärmeübertragung mit konstantem Druck (idealisiertes Modell) von einer externen Quelle (Verbrennung des Kraftstoffs) an die Luft, während sich der Kolben in Richtung bewegt V 4 . Während des Konstantdruckprozesses tritt Energie in das System ein, wenn Wärme Q hinzugefügt wird , und ein Teil der Arbeit wird durch Bewegen des Kolbens erledigt.
- Isentropische Expansion (Krafthub) – Das Gas expandiert adiabatisch von Zustand 4 zu Zustand 5, wenn sich der Kolben von V 3 zum unteren Totpunkt bewegt . Das Gas wirkt auf die Umgebung (Kolben) und verliert eine Menge an interner Energie, die der Arbeit entspricht, die das System verlässt. Auch hier bleibt die Entropie unverändert.
- Isochore Dekompression (Abgashub) – In dieser Phase wird der Zyklus durch einen Prozess mit konstantem Volumen abgeschlossen, bei dem der Luft Wärme entzogen wird, während sich der Kolben im unteren Totpunkt befindet. Der Arbeitsgasdruck fällt augenblicklich von Punkt 5 auf Punkt 1 ab. Das Auslassventil öffnet an Punkt 5. Der Auslasshub erfolgt unmittelbar nach dieser Dekompression. Wenn sich der Kolben bei geöffnetem Auslassventil vom unteren Totpunkt (Punkt 1) zum oberen Totpunkt (Punkt 0) bewegt, wird das Gasgemisch in die Atmosphäre abgelassen und der Prozess beginnt von neuem.
Während des Doppelzyklus wird vom Gas zwischen den Zuständen 1 und 2 ( i sentropische Kompression ) am Gas gearbeitet . Die Arbeit am Kolben erfolgt zwischen den Stufen 2 und 3 ( i sobarische Wärmezufuhr ) und zwischen den Stufen 2 und 3 ( i sentropische Expansion ). Der Unterschied zwischen der vom Gas geleisteten Arbeit und der am Gas geleisteten Arbeit ist das vom Kreislauf erzeugte Netz und entspricht der von der Kreislaufkurve umschlossenen Fläche. Die durch die Zykluszeiten erzeugte Arbeit multipliziert mit der Geschwindigkeit des Zyklus (Zyklen pro Sekunde) entspricht der vom Dieselmotor erzeugten Leistung.
Isentropischer Prozess
Ein isentropischer Prozess ist ein thermodynamischer Prozess , bei dem die Entropie des Fluids oder Gases konstant bleibt. Dies bedeutet, dass der isentrope Prozess ein Sonderfall eines adiabatischen Prozesses ist, bei dem keine Wärme- oder Materieübertragung stattfindet. Es ist ein reversibler adiabatischer Prozess . Die Annahme, dass keine Wärmeübertragung stattfindet, ist sehr wichtig, da wir die adiabatische Näherung nur in sehr schnellen Prozessen verwenden können .
Isentropischer Prozess und das erste Gesetz
Für ein geschlossenes System können wir den ersten Hauptsatz der Thermodynamik in Bezug auf die Enthalpie schreiben :
dH = dQ + Vdp
oder
dH = TdS + Vdp
Isentropischer Prozess (dQ = 0):
dH = Vdp → W = H 2 – H 1 → H 2 – H 1 = C p (T 2 – T 1 ) (für ideales Gas )
Isentropischer Prozess des idealen Gases
Der isentrope Prozess (ein Sonderfall des adiabatischen Prozesses) kann mit dem idealen Gasgesetz ausgedrückt werden als:
pV κ = konstant
oder
p 1 V 1 κ = p 2 V 2 κ
wobei κ = c p / c v das Verhältnis der spezifischen Wärme (oder Wärmekapazitäten ) für das Gas ist. Eine für konstanten Druck (c p ) und eine für konstantes Volumen (c v ) . Es ist zu beachten, dass dieses Verhältnis & kgr; = c p / c v ein Faktor bei der Bestimmung der Schallgeschwindigkeit in einem Gas und anderen adiabatischen Prozessen ist.
Isochorischer Prozess
Ein isochorer Prozess ist ein thermodynamischer Prozess, bei dem das Volumen des geschlossenen Systems konstant bleibt (V = const). Es beschreibt das Verhalten von Gas im Behälter, das nicht verformt werden kann. Da das Volumen konstant bleibt, funktioniert der Wärmeübergang in oder aus dem System nicht mit dem p∆V , sondern ändert nur die innere Energie (die Temperatur) des Systems.
Isochorischer Prozess und das erste Gesetz
Die klassische Form des ersten Hauptsatzes der Thermodynamik ist die folgende Gleichung:
dU = dQ – dW
In dieser Gleichung ist dW gleich dW = pdV und ist bekannt als die Grenz Arbeit . Dann:
dU = dQ – pdV
Beim isochoren Prozess und beim idealen Gas wird die gesamte dem System zugeführte Wärme zur Erhöhung der inneren Energie verwendet.
Isochorischer Prozess (pdV = 0):
dU = dQ (für ideales Gas)
dU = 0 = Q – W → W = Q (für ideales Gas)
Isochorischer Prozess des idealen Gases
Der isochore Prozess kann mit dem idealen Gasgesetz ausgedrückt werden als:
oder
In einem pV-Diagramm erfolgt der Prozess entlang einer horizontalen Linie mit der Gleichung V = konstant.
Siehe auch: Guy-Lussacs Gesetz
Isobarer Prozess
Ein isobarer Prozess ist ein thermodynamischer Prozess , bei dem der Druck des Systems konstant bleibt (p = const). Die Wärmeübertragung in oder aus dem System funktioniert zwar, verändert aber auch die innere Energie des Systems.
Da sich die innere Energie (dU) und das Systemvolumen (∆V) ändern, verwenden Ingenieure häufig die Enthalpie des Systems, die wie folgt definiert ist:
H = U + pV
Isobarer Prozess und das erste Gesetz
Die klassische Form des ersten Hauptsatzes der Thermodynamik ist die folgende Gleichung:
dU = dQ – dW
In dieser Gleichung ist dW gleich dW = pdV und ist bekannt als die Grenz Arbeit . Bei einem isobaren Prozess und dem idealen Gas wird ein Teil der dem System zugeführten Wärme für die Arbeit verwendet, und ein Teil der zugeführten Wärme erhöht die innere Energie (erhöht die Temperatur). Daher ist es zweckmäßig, die Enthalpie anstelle der inneren Energie zu verwenden.
Isobarer Prozess (Vdp = 0):
dH = dQ → Q = H 2 – H 1
Bei konstanter Entropie , dh im isentropischen Prozess, entspricht die Enthalpieänderung der Flussprozessarbeit, die am oder vom System ausgeführt wird.
Isobarer Prozess des idealen Gases
Der isobare Prozess kann mit dem idealen Gasgesetz ausgedrückt werden als:
oder
In einem pV-Diagramm erfolgt der Prozess entlang einer horizontalen Linie (Isobare genannt) mit der Gleichung p = Konstante.
Siehe auch: Charles ‘Gesetz
Wärmewirkungsgrad für Doppelzyklus
Im allgemeinen wird die thermischen Wirkungsgrad , η th , ein Wärmekraftmaschine ist als das Verhältnis der definierten Arbeits es tut, W , an den Wärmeeingang bei der hohen Temperatur, Q H .
Der thermische Wirkungsgrad , η th , stellt den Anteil an Wärme , Q H , die konvertiert wird , zu arbeiten . Da Energie nach dem ersten Hauptsatz der Thermodynamik eingespart wird und Energie nicht vollständig in Arbeit umgewandelt werden kann , muss der Wärmeeintrag Q H gleich der geleisteten Arbeit W plus der Wärme sein, die als Abwärme Q C an die abgegeben werden muss Umgebung. Daher können wir die Formel für den thermischen Wirkungsgrad wie folgt umschreiben:
Daher ist die hinzugefügte und abgegebene Wärme gegeben durch:
Q add-1 = mc v (T 3 – T 2 )
Q add-2 = mc p (T 4 – T 3 )
Q out = mc v (T 5 – T 1 )
Daher beträgt der thermische Wirkungsgrad für einen Doppelzyklus:
……………………………………………………………………………………………………………………………….
Dieser Artikel basiert auf der maschinellen Übersetzung des englischen Originalartikels. Weitere Informationen finden Sie im Artikel auf Englisch. Sie können uns helfen. Wenn Sie die Übersetzung korrigieren möchten, senden Sie diese bitte an: translations@nuclear-power.com oder füllen Sie das Online-Übersetzungsformular aus. Wir bedanken uns für Ihre Hilfe und werden die Übersetzung so schnell wie möglich aktualisieren. Danke.