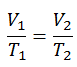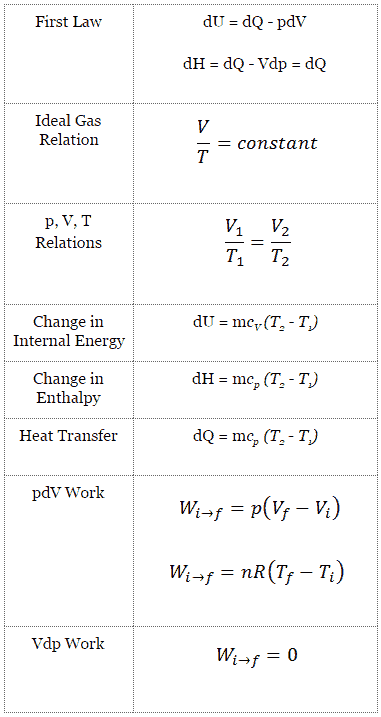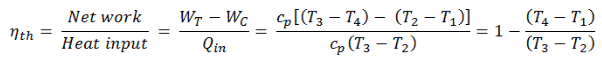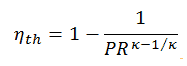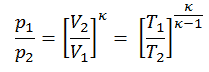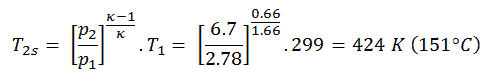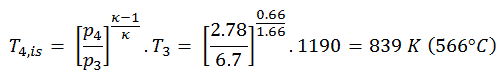Joule-Kreisprozess – Brayton-Kreisprozess – Turbinenmotor
1872 brachte der amerikanische Ingenieur George Bailey Brayton die Untersuchung von Wärmekraftmaschinen voran , indem er einen Verbrennungsmotor mit konstantem Druck patentierte, bei dem zunächst verdampftes Gas, später flüssige Brennstoffe wie Kerosin verwendet wurden. Diese Wärmekraftmaschine ist als ” Brayton’s Ready Motor ” bekannt . Dies bedeutet, dass der ursprüngliche Brayton-Motor anstelle einer Gasturbine und eines Gaskompressors einen Kolbenkompressor und einen Kolbenexpander verwendete.
Heute moderne Gasturbinenmotoren und Luftholen Strahltriebwerke sind auch ein Konstantdruck – Wärmemotoren, deshalb wir ihre Thermodynamik vom beschreiben Zyklus Brayton . Im Allgemeinen beschreibt der Brayton-Zyklus die Funktionsweise einer Wärmekraftmaschine mit konstantem Druck .
Es ist einer der häufigsten thermodynamischen Zyklen , die in Gasturbinenkraftwerken oder in Flugzeugen zu finden sind. Im Gegensatz zum Carnot-Zyklus führt der Brayton-Zyklus keine isothermen Prozesse aus , da diese sehr langsam ausgeführt werden müssen. In einem idealen Brayton- Zyklus durchläuft das System, das den Zyklus ausführt, eine Reihe von vier Prozessen: zwei isentrope (reversible adiabatische) Prozesse, die sich mit zwei isobaren Prozessen abwechseln.
Da das Carnot-Prinzip besagt, dass kein Motor effizienter sein kann als ein reversibler Motor ( eine Carnot-Wärmekraftmaschine ), der zwischen denselben Hochtemperatur- und Niedertemperaturspeichern betrieben wird, muss eine auf dem Brayton-Zyklus basierende Gasturbine einen geringeren Wirkungsgrad aufweisen als der Carnot-Wirkungsgrad.
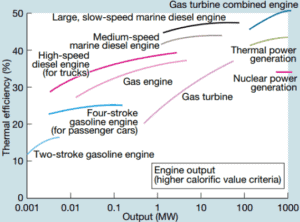
Eine große einzyklische Gasturbine erzeugt typischerweise beispielsweise 300 Megawatt Strom und hat einen thermischen Wirkungsgrad von 35–40%. Moderne kombinierte Gasturbinenanlagen (CCGT), bei denen der thermodynamische Zyklus aus zwei Kraftwerkszyklen besteht (z. B. der Brayton-Zyklus und der Rankine-Zyklus), können einen thermischen Wirkungsgrad von etwa 55% erreichen.
Arten von Gasturbinen
Im Allgemeinen werden Wärmekraftmaschinen und auch Gasturbinen nach einem Verbrennungsort wie folgt eingeteilt:
- Turbinen mit innerer Verbrennung . Die meisten Gasturbinen sind Verbrennungsmotoren. In diesen Turbinen wird die hohe Temperatur durch Verbrennen des Kraftstoff-Luft-Gemisches in der Brennkammer erreicht.
- Turbinen mit externer Verbrennung . In diesen Turbinen wird normalerweise ein Wärmetauscher verwendet und nur sauberes Medium ohne Verbrennungsprodukte wandert durch die Leistungsturbine. Da die Turbinenschaufeln keinen Verbrennungsprodukten ausgesetzt sind, können Kraftstoffe von viel geringerer Qualität (und daher billiger) verwendet werden. Diese Turbinen haben normalerweise einen geringeren thermischen Wirkungsgrad als Turbinen mit innerer Verbrennung.
Arten des Brayton-Zyklus
Öffnen Sie den Brayton-Zyklus (Schlüsselwörter)
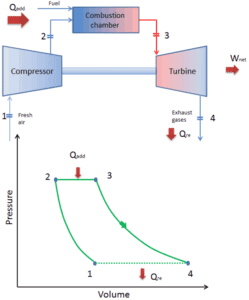
Da die meisten Gasturbinen auf dem Brayton-Zyklus mit innerer Verbrennung basieren (z. B. Strahltriebwerke), basieren sie auf dem offenen Brayton-Zyklus . In diesem Zyklus wird Luft aus der Umgebungsatmosphäre durch den Kompressor auf einen höheren Druck und eine höhere Temperatur komprimiert. In der Brennkammer wird Luft weiter erhitzt, indem das Kraftstoff-Luft-Gemisch im Luftstrom verbrannt wird. Verbrennungsprodukte und Gase dehnen sich in der Turbine entweder auf nahezu atmosphärischen Druck (Triebwerke, die mechanische oder elektrische Energie erzeugen) oder auf einen von den Strahltriebwerken benötigten Druck aus. Durch den offenen Brayton-Kreislauf werden die Gase direkt in die Atmosphäre abgegeben .
Geschlossener Brayton-Zyklus
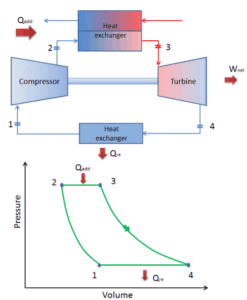
In einem geschlossenen Brayton-Kreislauf zirkuliert das Arbeitsmedium (z. B. Helium) in der Schleife und das aus der Turbine ausgestoßene Gas wird wieder in den Kompressor eingeleitet. In diesen Turbinen wird üblicherweise ein Wärmetauscher (externe Verbrennung) verwendet und nur sauberes Medium ohne Verbrennungsprodukte wandert durch die Leistungsturbine. Der geschlossene Brayton-Kreislauf wird beispielsweise in Gasturbinen mit geschlossenem Kreislauf und gasgekühlten Hochtemperaturreaktoren verwendet.
Reverse Brayton Cycle – Brayton Refrigeration Cycle
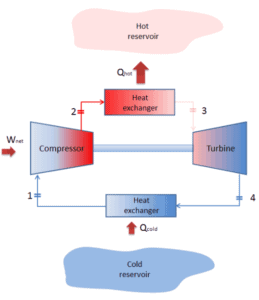
Ein Brayton-Zyklus, der in umgekehrter Richtung gefahren wird, ist als umgekehrter Brayton-Zyklus bekannt. Sein Zweck ist es, Wärme von einem kälteren zu einem heißeren Körper zu transportieren, anstatt Arbeit zu produzieren. In Übereinstimmung mit dem zweiten Hauptsatz der Thermodynamik kann Wärme nicht spontan vom kalten zum heißen System fließen , ohne dass externe Arbeiten am System durchgeführt werden. Wärme kann vom kälteren zum heißeren Körper fließen, jedoch nur, wenn sie durch eine externe Arbeit gezwungen wird. Genau das leisten Kühlschränke und Wärmepumpen. Diese werden von Elektromotoren angetrieben, für deren Betrieb Arbeiten aus ihrer Umgebung erforderlich sind. Einer der möglichen Zyklen ist ein umgekehrter Brayton-Zyklus, der dem gewöhnlichen Brayton-Zyklus ähnlich ist, jedoch über die Netzwerkeingabe rückwärts gefahren wird. Dieser Kreislauf wird auch als Gaskühlkreislauf oder Bell-Coleman-Kreislauf bezeichnet. Diese Art von Zyklus wird häufig in Düsenflugzeugen für Klimaanlagen verwendet, die Luft von den Triebwerkskompressoren verwenden. Es ist auch in der LNG-Industrie weit verbreitet, wo der größte umgekehrte Brayton-Zyklus zum Unterkühlen von LNG unter Verwendung von 86 MW Leistung aus einem Gasturbinen-Kompressor und Stickstoff-Kältemittel dient.
Brayton-Zyklus – Prozesse
In einem geschlossenen idealen Brayton- Zyklus durchläuft das System, das den Zyklus ausführt, eine Reihe von vier Prozessen: zwei isentrope (reversible adiabatische) Prozesse, die sich mit zwei isobaren Prozessen abwechseln:
-
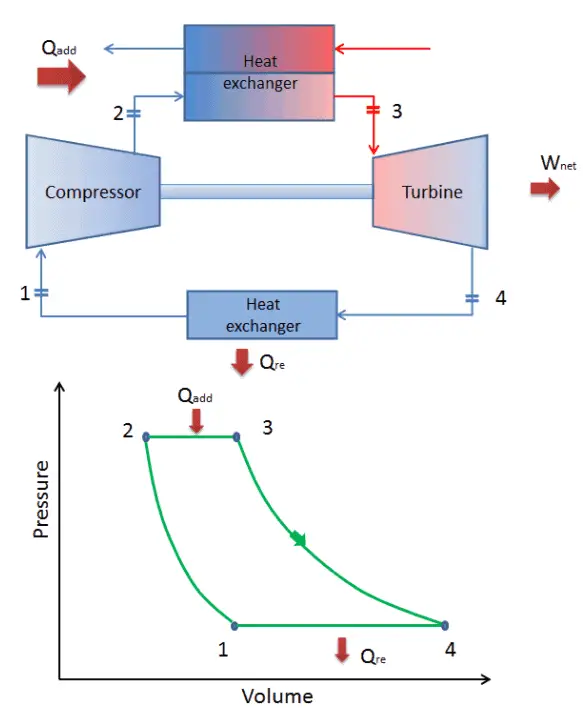
geschlossener Brayton-Zyklus Isentropische Kompression (Kompression in einem Kompressor) – Das Arbeitsgas (z. B. Helium) wird vom Kompressor (normalerweise einem Axialkompressor) adiabatisch von Zustand 1 in Zustand 2 komprimiert. Die Umgebung arbeitet am Gas, erhöht seine innere Energie (Temperatur) und komprimiert es (erhöht seinen Druck). Andererseits bleibt die Entropie unverändert. Die für den Kompressor erforderliche Arbeit ist gegeben durch W C = H 2 – H 1 .
- Isobare Wärmezufuhr (in einem Wärmetauscher) – In dieser Phase (zwischen Zustand 2 und Zustand 3) erfolgt eine Wärmeübertragung mit konstantem Druck von einer externen Quelle auf das Gas, da die Kammer zum Ein- und Ausströmen geöffnet ist. In einem offenen idealen Brayton-Zyklus läuft die Druckluft dann durch eine Brennkammer, in der Kraftstoff verbrannt und Luft oder ein anderes Medium erwärmt wird (2 → 3). Es ist ein Prozess mit konstantem Druck, da die Kammer zum Ein- und Ausströmen geöffnet ist. Die hinzugefügte Nettowärme ist gegeben durch Q add = H 3 – H 2
- Isentropische Expansion (Expansion in einer Turbine) – Das komprimierte und erhitzte Gas expandiert adiabatisch von Zustand 3 zu Zustand 4 in einer Turbine. Das Gas wirkt auf die Umgebung (Schaufeln der Turbine) und verliert eine Menge an interner Energie, die der Arbeit entspricht, die das System verlässt. Die von der Turbine geleistete Arbeit ist gegeben durch W T = H 4 – H 3 . Auch hier bleibt die Entropie unverändert.
- Isobare Wärmeabgabe (in einem Wärmetauscher) – In dieser Phase wird der Zyklus durch einen Prozess mit konstantem Druck abgeschlossen, bei dem Wärme aus dem Gas abgegeben wird. Die Arbeitsgastemperatur sinkt von Punkt 4 auf Punkt 1. Die abgegebene Nettowärme ergibt sich aus Q re = H 4 – H 1
Während eines Brayton-Zyklus wird vom Kompressor zwischen den Zuständen 1 und 2 ( i sentropische Kompression ) am Gas gearbeitet . Die Arbeit wird durch das Gas in der Turbine zwischen den Stufen 3 und 4 erledigt ( i sentropische Expansion ). Die Differenz zwischen der vom Gas geleisteten Arbeit und der am Gas geleisteten Arbeit ist das vom Zyklus erzeugte Netz und entspricht der von der Zykluskurve eingeschlossenen Fläche (im pV-Diagramm).
Wie zu sehen ist, ist es zweckmäßig, bei der Analyse dieses thermodynamischen Zyklus die Enthalpie oder die spezifische Enthalpie zu verwenden und das erste Gesetz in Bezug auf die Enthalpie auszudrücken . Diese Form des Gesetzes vereinfacht die Beschreibung der Energieübertragung . Bei konstantem Druck entspricht die Enthalpieänderung der Energie , die durch Erhitzen aus der Umgebung übertragen wird:
Isobarer Prozess (Vdp = 0):
dH = dQ → Q = H 2 – H 1
Bei konstanter Entropie , dh im isentropischen Prozess, entspricht die Enthalpieänderung der am oder vom System durchgeführten Flussprozessarbeit :
Isentropischer Prozess (dQ = 0):
dH = Vdp → W = H 2 – H 1
Siehe auch: Warum verwenden Energieingenieure Enthalpie? Antwort: dH = dQ + Vdp
Isentropischer Prozess
Ein isentropischer Prozess ist ein thermodynamischer Prozess , bei dem die Entropie des Fluids oder Gases konstant bleibt. Dies bedeutet, dass der isentrope Prozess ein Sonderfall eines adiabatischen Prozesses ist, bei dem keine Wärme- oder Materieübertragung stattfindet. Es ist ein reversibler adiabatischer Prozess . Die Annahme, dass keine Wärmeübertragung stattfindet, ist sehr wichtig, da wir die adiabatische Näherung nur in sehr schnellen Prozessen verwenden können .
Isentropischer Prozess und das erste Gesetz
Für ein geschlossenes System können wir den ersten Hauptsatz der Thermodynamik in Bezug auf die Enthalpie schreiben :
dH = dQ + Vdp
oder
dH = TdS + Vdp
Isentropischer Prozess (dQ = 0):
dH = Vdp → W = H 2 – H 1 → H 2 – H 1 = C p (T 2 – T 1 ) (für ideales Gas )
Isentropischer Prozess des idealen Gases
Der isentrope Prozess (ein Sonderfall des adiabatischen Prozesses) kann mit dem idealen Gasgesetz ausgedrückt werden als:
pV κ = konstant
oder
p 1 V 1 κ = p 2 V 2 κ
wobei κ = c p / c v das Verhältnis der spezifischen Wärme (oder Wärmekapazitäten ) für das Gas ist. Eine für konstanten Druck (c p ) und eine für konstantes Volumen (c v ) . Es ist zu beachten, dass dieses Verhältnis & kgr; = c p / c v ein Faktor bei der Bestimmung der Schallgeschwindigkeit in einem Gas und anderen adiabatischen Prozessen ist.
Isobarer Prozess
Ein isobarer Prozess ist ein thermodynamischer Prozess , bei dem der Druck des Systems konstant bleibt (p = const). Die Wärmeübertragung in oder aus dem System funktioniert zwar, verändert aber auch die innere Energie des Systems.
Da sich die innere Energie (dU) und das Systemvolumen (∆V) ändern, verwenden Ingenieure häufig die Enthalpie des Systems, die wie folgt definiert ist:
H = U + pV
Isobarer Prozess und das erste Gesetz
Die klassische Form des ersten Hauptsatzes der Thermodynamik ist die folgende Gleichung:
dU = dQ – dW
In dieser Gleichung ist dW gleich dW = pdV und ist bekannt als die Grenz Arbeit . Bei einem isobaren Prozess und dem idealen Gas wird ein Teil der dem System zugeführten Wärme für die Arbeit verwendet, und ein Teil der zugeführten Wärme erhöht die innere Energie (erhöht die Temperatur). Daher ist es zweckmäßig, die Enthalpie anstelle der inneren Energie zu verwenden.
Isobarer Prozess (Vdp = 0):
dH = dQ → Q = H 2 – H 1
Bei konstanter Entropie , dh im isentropischen Prozess, entspricht die Enthalpieänderung der Flussprozessarbeit, die am oder vom System ausgeführt wird.
Isobarer Prozess des idealen Gases
Der isobare Prozess kann mit dem idealen Gasgesetz ausgedrückt werden als:
oder
In einem pV-Diagramm erfolgt der Prozess entlang einer horizontalen Linie (Isobare genannt) mit der Gleichung p = Konstante.
Siehe auch: Charles ‘Gesetz
Brayton-Zyklus – pV, Ts-Diagramm
Der Brayton-Zyklus wird häufig in einem Druckvolumendiagramm ( pV-Diagramm ) und in einem Temperatur-Entropie-Diagramm ( Ts-Diagramm ) aufgezeichnet .
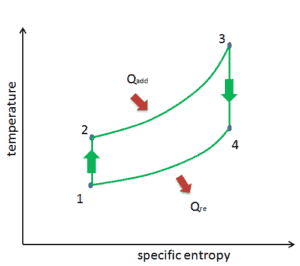
Wenn sie auf einem aufgetragen P-V-Diagramm , die isobare Verfahren der isobare Leitungen für das Gas (die horizontalen Linien) folgen, adiabatische Prozesse zwischen diesen horizontalen Linien bewegen , und die durch den gesamten Zyklus hinweg Pfad begrenzt Bereich stellt die gesamte Arbeit , die während einem getan werden kann , Zyklus.
Das Temperatur-Entropie-Diagramm (Ts-Diagramm), in dem der thermodynamische Zustand durch einen Punkt in einem Diagramm mit spezifischen Entropien als horizontale Achse und absoluter Temperatur (T) als vertikaler Achse angegeben wird. Ts-Diagramme sind ein nützliches und allgemeines Werkzeug, insbesondere weil sie dazu beitragen, die Wärmeübertragung während eines Prozesses zu visualisieren . Bei reversiblen (idealen) Prozessen ist die Fläche unter der Ts-Kurve eines Prozesses die Wärme , die während dieses Prozesses auf das System übertragen wird.
Thermische Effizienz des Brayton-Zyklus
Im allgemeinen wird die thermischen Wirkungsgrad , η th , ein Wärmekraftmaschine ist als das Verhältnis der definierten Arbeits es tut, W , an den Wärmeeingang bei der hohen Temperatur, Q H .
Der thermische Wirkungsgrad , η th , stellt den Anteil an Wärme , Q H , die konvertiert wird , zu arbeiten . Da Energie nach dem ersten Hauptsatz der Thermodynamik eingespart wird und Energie nicht vollständig in Arbeit umgewandelt werden kann , muss der Wärmeeintrag Q H gleich der geleisteten Arbeit W plus der Wärme sein, die als Abwärme Q C an die abgegeben werden muss Umgebung. Daher können wir die Formel für den thermischen Wirkungsgrad wie folgt umschreiben:
Dies ist eine sehr nützliche Formel, aber hier drücken wir den thermischen Wirkungsgrad unter Verwendung des ersten Gesetzes in Bezug auf die Enthalpie aus .
Um den thermischen Wirkungsgrad des Brayton-Zyklus (einzelner Kompressor und einzelne Turbine) zu berechnen, verwenden Ingenieure den ersten Hauptsatz der Thermodynamik eher in Bezug auf die Enthalpie als in Bezug auf die innere Energie.
Das erste Gesetz in Bezug auf die Enthalpie lautet:
dH = dQ + Vdp
In dieser Gleichung ist der Begriff Vdp eine Flussprozessarbeit. Diese Arbeit, Vdp , wird für Open-Flow-Systeme wie eine Turbine oder eine Pumpe verwendet, bei denen ein „dp“ vorliegt , dh eine Druckänderung. Es gibt keine Änderungen in der Lautstärke . Wie zu sehen ist, vereinfacht diese Form des Gesetzes die Beschreibung der Energieübertragung .
Es gibt Ausdrücke in Bezug auf bekanntere Variablen wie Temperatur und Druck :
dH = C p dT + V (1-αT) dp
Dabei ist C p die Wärmekapazität bei konstantem Druck und α der Koeffizient der (kubischen) Wärmeausdehnung. Für ideales Gas ist αT = 1 und daher:
dH = C p dT
Bei konstantem Druck entspricht die Enthalpieänderung der Energie , die durch Erhitzen aus der Umgebung übertragen wird:
Isobarer Prozess (Vdp = 0):
dH = dQ → Q = H 3 – H 2 → H 3 – H 2 = C p (T 3 – T 2 )
Bei konstanter Entropie , dh im isentropischen Prozess, entspricht die Enthalpieänderung der am oder vom System durchgeführten Flussprozessarbeit :
Isentropischer Prozess (dQ = 0):
dH = Vdp → W = H 4 – H 3 → H 4 – H 3 = C p (T 4 – T 3 )
Die Enthalpie kann durch Teilen durch die Masse zu einer intensiven oder spezifischen Variablen gemacht werden . Ingenieure verwenden die spezifische Enthalpie in der thermodynamischen Analyse mehr als die Enthalpie selbst.
Nehmen wir nun den idealen Brayton-Zyklus an , der die Funktionsweise einer Wärmekraftmaschine mit konstantem Druck beschreibt. Moderne Gasturbinentriebwerke und luftatmende Strahltriebwerke folgen ebenfalls dem Brayton-Zyklus. Dieser Zyklus besteht aus vier thermodynamischen Prozessen:
-

Brayton-Zyklus – Ts-Diagramm isentropische Kompression – Umgebungsluft wird in den Kompressor gesaugt und dort unter Druck gesetzt (1 → 2). Die für den Kompressor erforderliche Arbeit ist gegeben durch W C = H 2 – H 1 .
- isobare Wärmezufuhr – Die Druckluft strömt dann durch eine Brennkammer, in der Kraftstoff verbrannt und Luft oder ein anderes Medium erwärmt wird (2 → 3). Es ist ein Prozess mit konstantem Druck, da die Kammer zum Ein- und Ausströmen geöffnet ist. Die hinzugefügte Nettowärme ist gegeben durch Q add = H 3 – H 2
- isentropische Expansion – Die erwärmte Druckluft dehnt sich dann auf der Turbine aus und gibt ihre Energie ab. Die von der Turbine geleistete Arbeit ist gegeben durch W T = H 4 – H 3
- isobare Wärmeabgabe – Die Restwärme muss abgeführt werden, um den Kreislauf zu schließen. Die abgegebene Nettowärme ist gegeben durch Q re = H 4 – H 1
Wie zu sehen ist, können wir solche Zyklen (ähnlich für den Rankine-Zyklus) unter Verwendung von Enthalpien vollständig beschreiben und berechnen.
Der thermische Wirkungsgrad eines solchen einfachen Brayton-Zyklus für ideales Gas und in Bezug auf spezifische Enthalpien kann nun in Form der Temperaturen ausgedrückt werden:
wo
- W T die Arbeit des Gases in der Turbine
- W C die Arbeit am Gas im Kompressor
- c p ist das Wärmekapazitätsverhältnis
Druckverhältnis – Brayton-Zyklus – Gasturbine
Der thermische Wirkungsgrad hinsichtlich des Verdichterdruckverhältnisses (PR = p 2 / p 1 ), welches der Parameter ist häufig verwendet:
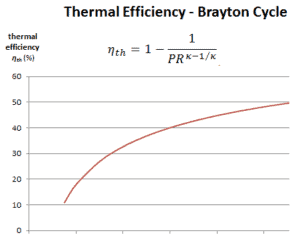 Im Allgemeinen ist das Erhöhen des Druckverhältnisses der direkteste Weg, um den thermischen Gesamtwirkungsgrad eines Brayton-Zyklus zu erhöhen, da sich der Zyklus dem Carnot-Zyklus nähert.
Im Allgemeinen ist das Erhöhen des Druckverhältnisses der direkteste Weg, um den thermischen Gesamtwirkungsgrad eines Brayton-Zyklus zu erhöhen, da sich der Zyklus dem Carnot-Zyklus nähert.
Nach dem Carnotschen Prinzip können durch Erhöhen der Gastemperatur höhere Wirkungsgrade erreicht werden.
Es gibt aber auch Grenzen für die Druckverhältnisse , die im Zyklus verwendet werden können. Die höchste Temperatur im Zyklus tritt am Ende des Verbrennungsprozesses auf und ist durch die maximale Temperatur begrenzt , der die Turbinenschaufeln standhalten können. Wie üblich setzen metallurgische Überlegungen (ca. 1700 K) dem thermischen Wirkungsgrad Obergrenzen.
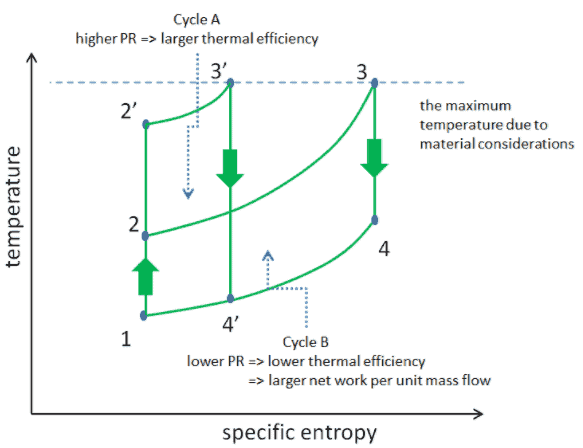
Berücksichtigen Sie die Auswirkung des Kompressordruckverhältnisses auf den thermischen Wirkungsgrad, wenn die Turbineneintrittstemperatur auf die maximal zulässige Temperatur beschränkt ist. Es gibt zwei Ts-Diagramme von Brayton-Zyklen mit der gleichen Turbineneintrittstemperatur, aber unterschiedlichen Kompressordruckverhältnissen auf dem Bild. Wie für eine Einlasstemperatur mit fester Turbine ersichtlich ist, nimmt die Nettoarbeitsleistung pro Zyklus (W net = W T – W C ) mit dem Druckverhältnis ( Zyklus A ) ab. Der Zyklus A hat jedoch die größere Effizienz.
Andererseits hat der Zyklus B eine größere Netzleistung pro Zyklus (im Diagramm eingeschlossener Bereich) und somit die größere entwickelte Netzleistung pro Einheit des Massenstroms. Die durch den Zyklus erzeugte Arbeit mal einem Massendurchsatz durch den Zyklus ist gleich der von der Gasturbine erzeugten Leistung.
Daher ist bei weniger Arbeitsleistung pro Zyklus (Zyklus A) ein größerer Massendurchsatz (also ein größeres System ) erforderlich, um die gleiche Leistungsabgabe aufrechtzuerhalten, was möglicherweise nicht wirtschaftlich ist. Dies ist die zentrale Überlegung bei der Auslegung von Gasturbinen, da hier Ingenieure den thermischen Wirkungsgrad und die Kompaktheit in Einklang bringen müssen. Bei den meisten gängigen Konstruktionen liegt das Druckverhältnis einer Gasturbine im Bereich von etwa 11 bis 16.
Verbesserung der thermischen Effizienz – Brayton-Zyklus
Es gibt verschiedene Methoden, wie der thermische Wirkungsgrad des Brayton-Zyklus verbessert werden kann. Unter der Annahme, dass die maximale Temperatur durch metallurgische Überlegungen begrenzt ist, sind diese Methoden:
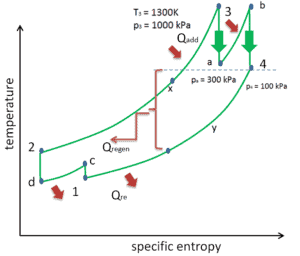
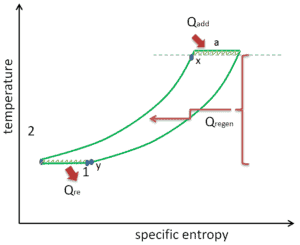
Aufwärmen, Ladeluftkühlung und Regeneration im Brayton-Zyklus
Wie bereits erwähnt, ergänzen Wiedererwärmung und Zwischenkühlung die Wärmerückgewinnung . An sich würden sie den thermischen Wirkungsgrad nicht notwendigerweise erhöhen. Wenn jedoch Zwischenkühlung oder Wiedererwärmung in Verbindung mit Wärmerückgewinnung verwendet wird, kann eine signifikante Steigerung des thermischen Wirkungsgrads erreicht werden und die Nettoarbeitsleistung wird ebenfalls erhöht. Dies erfordert eine Gasturbine mit zwei Kompressionsstufen und zwei Turbinenstufen.
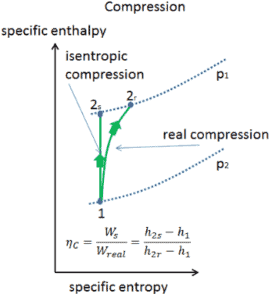
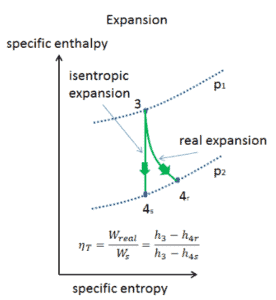
Isentropische Effizienz – Turbine, Kompressor
Die meisten Steady-Flow-Geräte (Turbinen, Kompressoren, Düsen) arbeiten unter adiabatischen Bedingungen , sind jedoch nicht wirklich isentrop, sondern für Berechnungszwecke eher als isentrop idealisiert. Wir definieren Parameter η T , η C , η N , als ein Verhältnis der realen Arbeit durch die Vorrichtung zu der Arbeit von Gerät , wenn es unter Bedingungen betrieben isentropen (im Falle der Turbine). Dieses Verhältnis ist als Wirkungsgrad von Isentropenturbine / Kompressor / Düse bekannt .
Siehe auch: Irreversibilität natürlicher Prozesse
Diese Parameter beschreiben, wie effizient sich eine Turbine, ein Kompressor oder eine Düse einer entsprechenden isentropischen Vorrichtung annähert. Dieser Parameter reduziert die Gesamteffizienz und die Arbeitsleistung. Für Turbinen beträgt der Wert von η T typischerweise 0,7 bis 0,9 (70–90%).
Brayton-Zyklus – Problem mit der Lösung
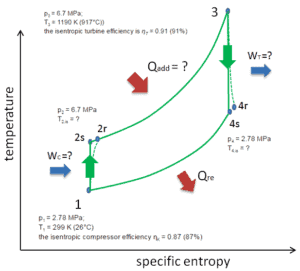
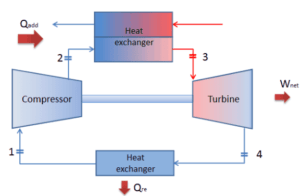 Nehmen wir den geschlossenen Brayton-Zyklus an , der einer der häufigsten thermodynamischen Zyklen ist, die in modernen Gasturbinentriebwerken zu finden sind. In diesem Fall wird eine Heliumgasturbine mit Einzelkompressor- und Einzelturbinenanordnung angenommen. Einer der Schlüsselparameter solcher Motoren ist die maximale Turbineneintrittstemperatur und das Kompressordruckverhältnis (PR = p 2 / p 1 ), die den thermischen Wirkungsgrad eines solchen Motors bestimmen.
Nehmen wir den geschlossenen Brayton-Zyklus an , der einer der häufigsten thermodynamischen Zyklen ist, die in modernen Gasturbinentriebwerken zu finden sind. In diesem Fall wird eine Heliumgasturbine mit Einzelkompressor- und Einzelturbinenanordnung angenommen. Einer der Schlüsselparameter solcher Motoren ist die maximale Turbineneintrittstemperatur und das Kompressordruckverhältnis (PR = p 2 / p 1 ), die den thermischen Wirkungsgrad eines solchen Motors bestimmen.
In dieser Turbine erhält die Hochdruckstufe Gas (Punkt 3 in der Abbildung) von einem Wärmetauscher:
- p 3 = 6,7 MPa;
- T 3 = 1190 K (917 ° C))
- der Wirkungsgrad der isentropischen Turbine beträgt η T = 0,91 (91%)
und entlüften Sie es zu einem anderen Wärmetauscher, wo der Ausgangsdruck ist (Punkt 4):
- p 4 = 2,78 MPa
- T 4 ist =?
Somit ist das Kompressordruckverhältnis gleich PR = 2,41. Außerdem wissen wir, dass der Kompressor in der Abbildung Gas (Punkt 1) erhält:
- p 1 = 2,78 MPa;
- T 1 = 299 K (26 ° C)
- der Wirkungsgrad des isentropischen Kompressors η K = 0,87 (87%).
Das Wärmekapazitätsverhältnis für Helium ist gleich = c p / c v = 1,66
- die vom Wärmetauscher zugeführte Wärme (zwischen 2 → 3)
- die Kompressorauslasstemperatur des Gases (T 2, ist )
- die eigentliche Arbeit an diesem Kompressor, wenn der Wirkungsgrad des isentropischen Kompressors η K = 0,87 (87%) beträgt
- die Turbinenaustrittstemperatur des Gases (T 4, ist )
- die eigentliche Arbeit dieser Turbine, wenn der Wirkungsgrad der isentropischen Turbine η T = 0,91 (91%) beträgt
- der thermische Wirkungsgrad dieses Zyklus
Lösung:
1) + 2)
Nach dem ersten Hauptsatz der Thermodynamik ist die hinzugefügte Nettowärme gegeben durch Q add, ex = H 3 – H 2 [kJ] oder Q add = C p (T 3 -T 2s ) , aber in diesem Fall wissen wir es nicht die Temperatur (T 2s ) am Auslass des Kompressors. Wir werden dieses Problem in intensiven Variablen lösen . Wir müssen die vorherige Gleichung (um η K einzuschließen ) unter Verwendung des Terms ( + h 1 – h 1 ) umschreiben, um:
Q add = h 3 – h 2 = h 3 – h 1 – (h 2s – h 1 ) / η K [kJ / kg]
Q addiere = c p (T 3 -T 1 ) – (c p (T 2s -T 1 ) / η K )
Dann berechnen wir die Temperatur T 2s unter Verwendung der p, V, T-Beziehung (aus dem idealen Gasgesetz ) für den adiabatischen Prozess zwischen (1 → 2).
In dieser Gleichung ist der Faktor für Helium gleich = c p / c v = 1,66. Aus der vorherigen Gleichung folgt, dass die Kompressorauslasstemperatur T 2s ist:
Mit dieser Temperatur und dem Wirkungsgrad des isentropischen Kompressors können wir die vom Wärmetauscher zugeführte Wärme berechnen:Q add = c p (T 3 -T 1 ) – (c p (T 2s -T 1 ) / η K ) = 5200. (1190 – 299) – 5200. (424-299) / 0,87 = 4,633 MJ / kg – 0,747 MJ / kg = 3,886 MJ / kg
3)
Die Arbeit des Kompressors am Gas im isentropischen Kompressionsprozess ist:
W C, s = c p (T 2s – T 1 ) = 5200 × (424 – 299) = 0,650 MJ / kg
Die eigentliche Arbeit, die der Kompressor bei der adiabatischen Kompression am Gas leistet, ist dann:
W C, real = c p (T 2s – T 1 ). η C = 5200 x (424 – 299) / 0,87 = 0,747 MJ / kg
4)
Die Turbinenaustrittstemperatur des Gases T 4 kann unter Verwendung der gleichen p, V, T-Beziehung wie in 2) berechnet werden , jedoch zwischen den Zuständen 3 und 4:
Aus der vorhergehenden Gleichung folgt, dass die Austrittstemperatur des Gases T 4 ist:
5)
Die Arbeit der Gasturbine bei der isentropischen Expansion ist dann:
W T, s = c p (T 3 – T 4 s ) = 5200 × (1190–839) = 1,825 MJ / kg
Die eigentliche Arbeit der Gasturbine bei der adiabatischen Expansion ist dann:
W T, real = c p (T 3 – T 4 s ). η T = 5200 x (1190 – 839) x 0,91 = 1,661 MJ / kg
6)
Wie im vorherigen Abschnitt abgeleitet, ist der thermische Wirkungsgrad eines idealen Brayton-Zyklus eine Funktion des Druckverhältnisses und von κ :
deshalb
η th = 0,295 = 29,5%
Der thermische Wirkungsgrad kann auch anhand der Arbeit und der Wärme (ohne η K ) berechnet werden :
η th, s = ( W T, s – W C, s ) / Q add, s = (1,825 – 0,650) / 3,983 = 0,295 = 29,5%
Schließlich beträgt der thermische Wirkungsgrad einschließlich des Wirkungsgrads der isentropischen Turbine / des Kompressors:
η th, real = ( W T, real – W C, real ) / Q add = (1,661 – 0,747) / 3,886 = 0,235 = 23,5%
……………………………………………………………………………………………………………………………….
Dieser Artikel basiert auf der maschinellen Übersetzung des englischen Originalartikels. Weitere Informationen finden Sie im Artikel auf Englisch. Sie können uns helfen. Wenn Sie die Übersetzung korrigieren möchten, senden Sie diese bitte an: translations@nuclear-power.com oder füllen Sie das Online-Übersetzungsformular aus. Wir bedanken uns für Ihre Hilfe und werden die Übersetzung so schnell wie möglich aktualisieren. Danke.