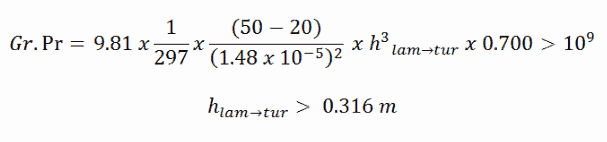Was ist Rayleigh-Zahl
Die Rayleigh-Zahl ist eine dimensionslose Zahl, benannt nach Lord Rayleigh. Die Rayleigh-Zahl ist eng mit der Grashof-Zahl verwandt, und beide Zahlen werden verwendet, um die natürliche Konvektion (Gr) und die Wärmeübertragung durch natürliche Konvektion (Ra) zu beschreiben. Die Rayleigh-Zahl ist einfach definiert als das Produkt der Grashof-Zahl , die die Beziehung zwischen Auftrieb und Viskosität innerhalb einer Flüssigkeit beschreibt, und der Prandtl-Zahl , die die Beziehung zwischen Impulsdiffusionsvermögen und thermischem Diffusionsvermögen beschreibt.
Ra x = Gr x . Pr
Die Grashof-Zahl ist definiert als das Verhältnis von Auftriebskraft zu viskoser Kraft, die auf ein Fluid in der Geschwindigkeitsgrenzschicht einwirkt. Ihre Rolle bei der natürlichen Konvektion entspricht in etwa der der Reynolds-Zahl bei der erzwungenen Konvektion. Natürliche Konvektion tritt auf, wenn diese Bewegung und Vermischung durch Dichteschwankungen verursacht wird, die sich aus Temperaturunterschieden innerhalb der Flüssigkeit ergeben. In der Regel nimmt die Dichte durch Temperaturanstieg ab und die Flüssigkeit steigt an. Diese Bewegung wird durch die Auftriebskraft verursacht. Die Hauptkraft, die sich der Bewegung widersetzt, ist die viskose Kraft. Die Grashof-Zahl ist ein Weg, um die entgegengesetzten Kräfte zu quantifizieren.
Die Rayleigh-Zahl wird verwendet, um die Wärmeübertragung in natürlicher Konvektion auszudrücken. Die Größe der Rayleigh-Zahl ist ein guter Hinweis darauf, ob die natürliche Konvektionsgrenzschicht laminar oder turbulent ist. Die einfachen empirischen Korrelationen für die durchschnittliche Nusselt-Zahl Nu in natürlicher Konvektion lauten wie folgt:
Nu x = C. Ra x n
Die Werte der Konstanten C und n hängen von der Geometrie der Oberfläche und dem Strömungsregime ab , das durch den Bereich der Rayleigh-Zahl charakterisiert ist . Der Wert von n beträgt normalerweise n = 1/4 für laminare Strömung und n = 1/3 für turbulente Strömung.
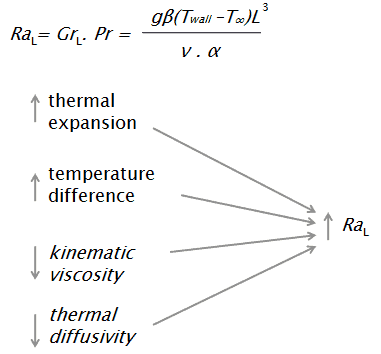
Die Rayleigh-Nummer ist wie folgt definiert:
wo:
g ist die Beschleunigung aufgrund der Schwerkraft der Erde
β ist der Wärmeausdehnungskoeffizient
T Wand ist die Wandtemperatur
T ∞ ist die Massentemperatur
L ist die vertikale Länge
α ist die Wärmeleitfähigkeit
ν ist die kinematische Viskosität.
Für Gase β = 1 / T, bei denen die Temperatur in K ist. Für Flüssigkeiten kann β berechnet werden, wenn eine Variation der Dichte mit der Temperatur bei konstantem Druck bekannt ist. Bei einer vertikalen flachen Platte wird die Strömung turbulent für den Wert von:
Ra x = Gr x . Pr> 10 9
Wie bei der erzwungenen Konvektion unterscheiden sich die mikrospischen Eigenschaften der Strömungs- und Konvektionskorrelationen im laminaren und im turbulenten Bereich deutlich.
Beispiel: Rayleigh-Nummer
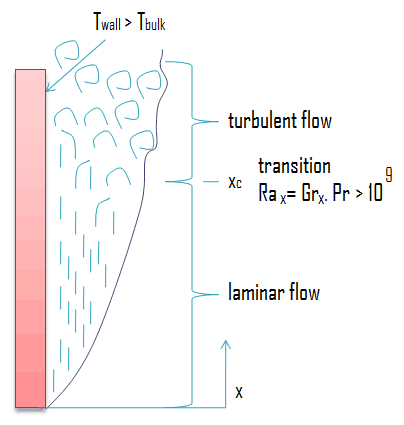Eine vertikale Platte wird in 20 ° C Luft bei 50 ° C gehalten. Bestimmen Sie die Höhe, in der die Grenzschicht turbulent wird, wenn bei Ra = Gr.Pr = 10 9 Turbulenzen auftreten .
Lösung:
Die für dieses Beispiel erforderlichen Eigenschaftswerte sind:
ν = 1,48 x 10 -5 m 2 / s
ρ = 1,17 kg / m 3
Pr = 0,700
β = 1 / (273 + 20) = 1/293
Wir wissen, dass die natürliche Zirkulation bei ungefähr Ra = Gr.Pr> 10 9 turbulent wird , was in der folgenden Höhe erfüllt ist:
……………………………………………………………………………………………………………………………….
Dieser Artikel basiert auf der maschinellen Übersetzung des englischen Originalartikels. Weitere Informationen finden Sie im Artikel auf Englisch. Sie können uns helfen. Wenn Sie die Übersetzung korrigieren möchten, senden Sie diese bitte an: translations@nuclear-power.com oder füllen Sie das Online-Übersetzungsformular aus. Wir bedanken uns für Ihre Hilfe und werden die Übersetzung so schnell wie möglich aktualisieren. Danke.
