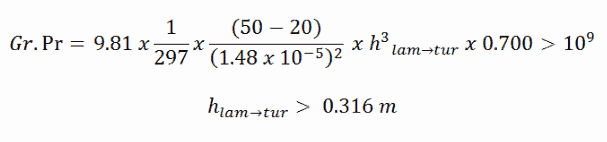Qu’est-ce que Nombre de Rayleigh? Définition

Quel est le nombre de Rayleigh

Le nombre de Rayleigh est un nombre sans dimension, nommé d’après Lord Rayleigh. Le nombre de Rayleigh  est étroitement lié au nombre de Grashof et les deux chiffres sont utilisés pour décrire la convection naturelle (Gr) et le transfert de chaleur par convection naturelle (Ra). Le  nombre de Rayleigh  est simplement défini comme le produit du nombre Grashof , qui décrit la relation entre la flottabilité et la viscosité dans un fluide, et le nombre de Prandtl , qui décrit la relation entre la diffusivité du moment et la diffusivité thermique.

Ra _x = Gr _x . Pr

Le  nombre de Grashof  est défini comme le rapport entre la force de flottabilité et la force visqueuse agissant sur un fluide dans la couche limite de vitesse. Son rôle dans la convection naturelle est à peu près identique à celui du  nombre de Reynolds  en convection forcée. La convection naturelle se produit si ce mouvement et ce mélange sont causés par des variations de densité résultant de différences de température dans le fluide. Habituellement, la densité diminue en raison d’une augmentation de la température et entraîne la montée du fluide. Ce mouvement est provoqué par la force de flottabilité. La force majeure qui résiste au mouvement est la force visqueuse. Le nombre Grashof est un moyen de quantifier les forces en présence.

Le nombre de Rayleigh est utilisé pour exprimer le transfert de chaleur en convection naturelle. La magnitude du nombre de Rayleigh indique bien si la couche limite de convection naturelle est laminaire ou turbulente. Les corrélations empiriques simples pour le nombre moyen de Nusselt, Nu, en convection naturelle sont de la forme:

Nu _x  = C. Ra _x ⁿ

Les valeurs des constantes C et n dépendent de la géométrie de la surface et du régime d’écoulement , qui est caractérisé par la plage du nombre de Rayleigh . La valeur de n est généralement n = 1/4 pour un écoulement laminaire et n = 1/3 pour un écoulement turbulent.

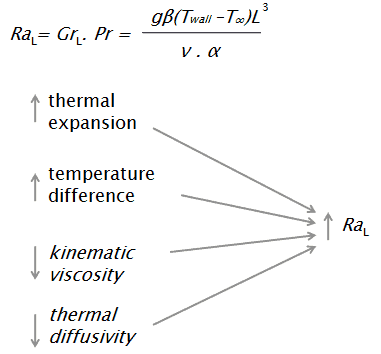
Le  nombre de Rayleigh est défini comme suit:

où:

g est l’accélération due à la gravité de la Terre

β est le coefficient de dilatation thermique

T _mur est la température du mur

T _∞ est la température globale

L est la longueur verticale

α est  la diffusivité thermique

ν est la viscosité cinématique.

Pour les gaz β = 1 / T où la température est en K. Pour les liquides, β peut être calculé si la variation de densité avec la température à pression constante est connue. Pour une plaque plane verticale, le flux devient turbulent pour une valeur de:

Ra _x  = Gr _x  . Pr> 10 ⁹ 

Comme dans la convection forcée, la nature microspique des corrélations d’écoulement et de convection est distinctement différente dans les régions laminaires et turbulentes .

Exemple: nombre de Rayleigh

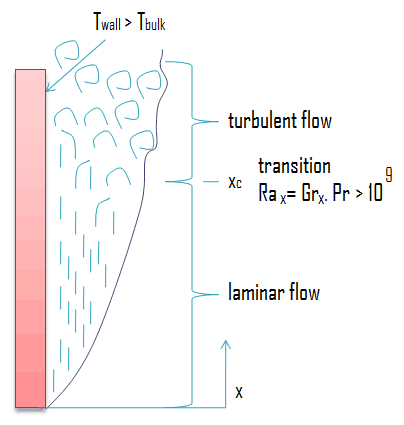Une plaque verticale est maintenue à 50 ° C dans 20 ° C d’air. Déterminez la hauteur à laquelle la couche limite deviendra turbulente si la turbulence s’installe à Ra = Gr.Pr = 10 ⁹ .

Solution:

Les valeurs de propriété requises pour cet exemple sont:

ν = 1,48 x 10 ^-5 m ² / s

ρ = 1,17 kg / m ³

Pr = 0,700

β = 1 / (273 + 20) = 1/293

Nous savons que la circulation naturelle devient turbulente à environ Ra = Gr.Pr> 10 ⁹ , ce qui est accompli à la hauteur suivante: