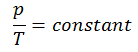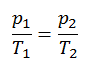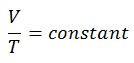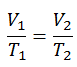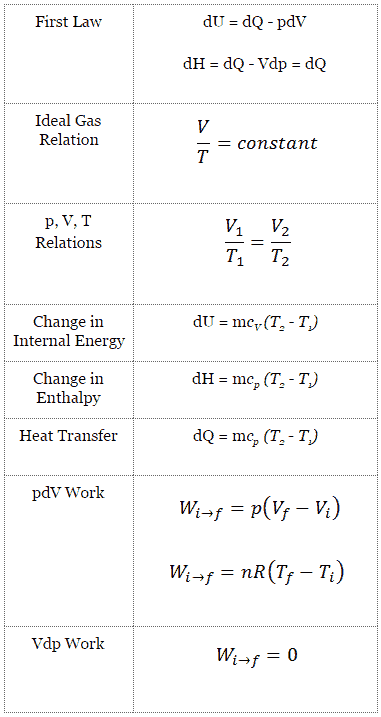Processus thermodynamiques en cycle diesel
Dans un cycle Diesel idéal, le système qui exécute le cycle est soumis à quatre processus: deux processus isentropiques (adiabatiques réversibles) alternés avec un processus isochore et un processus isobare.
Processus thermodynamiques en cycle diesel:
-
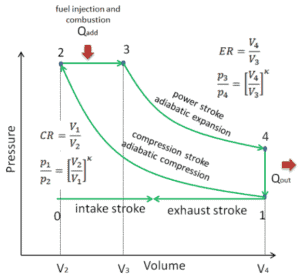
Diagramme pv d’un cycle diesel idéal Compression isentropique (course de compression) – L’air est comprimé de manière adiabatique de l’état 1 à l’état 2, le piston se déplaçant du point mort inférieur au point mort haut. Les environs travaillent sur le gaz, en augmentant son énergie interne (température) et en le comprimant. Par contre, l’entropie reste inchangée. L’évolution des volumes et de son rapport ( V 1 / V 2 ) est appelée taux de compression.
- Expansion isobare (phase d’allumage) – Dans cette phase (entre les états 2 et 3), un transfert de chaleur à pression constante (modèle idéalisé) s’effectue dans l’air à partir d’une source externe (combustion de carburant injecté) pendant que le piston se déplace vers la V 3 . Pendant le processus de pression constante, l’ énergie pénètre dans le système en tant que chaleur Q complément , et une partie de travail est effectué par le piston mobile.
- Expansion isentropique (course de puissance) – Le gaz se dilate de manière adiabatique de l’état 3 à l’état 4, le piston se déplaçant de V 3 au point mort bas. Le gaz fonctionne sur l’environnement (piston) et perd une quantité d’énergie interne égale au travail qui quitte le système. Encore une fois, l’entropie reste inchangée. Le rapport volumique ( V 4 / V 3 ) est appelé rapport de dilatation isentropique.
- Décompression isochorique (course d’échappement) – Dans cette phase, le cycle se termine par un processus à volume constant dans lequel la chaleur est rejetée de l’air pendant que le piston est au point mort bas. La pression de gaz de travail chute instantanément du point 4 au point 1. La soupape d’échappement s’ouvre au point 4. La course d’échappement se fait immédiatement après cette décompression. Lorsque le piston se déplace du point mort bas (point 1) au point mort haut (point 0) avec la soupape d’échappement ouverte, le mélange gazeux est évacué dans l’atmosphère et le processus recommence à nouveau.
Pendant le cycle Diesel, un travail est effectué sur le gaz par le piston entre les états 1 et 2 ( i compression sentropique ). Le travail se fait par le gaz sur le piston entre les étapes 2 et 3 ( i addition de chaleur sobarique ) et entre les étapes 2 et 3 ( i expansion sentropique ). La différence entre le travail effectué par le gaz et le travail effectué sur le gaz est le travail net produit par le cycle et il correspond à la zone délimitée par la courbe du cycle. Le travail produit par le cycle multiplie la vitesse du cycle (cycles par seconde) par la puissance produite par le moteur Diesel.
Processus isentropique
Un processus isentropique est un processus thermodynamique , dans lequel l’ entropie du fluide ou du gaz reste constante. Cela signifie que le processus isentropique est un cas particulier d’un processus adiabatique dans lequel il n’y a pas de transfert de chaleur ou de matière. Il s’agit d’un processus adiabatique réversible . L’hypothèse d’absence de transfert de chaleur est très importante, car nous ne pouvons utiliser l’approximation adiabatique que dans des processus très rapides .
Processus isentropique et première loi
Pour un système fermé, on peut écrire la première loi de la thermodynamique en termes d’enthalpie :
dH = dQ + Vdp
ou
dH = TdS + Vdp
Processus isentropique (dQ = 0):
dH = Vdp → W = H 2 – H 1 → H 2 – H 1 = C p (T 2 – T 1 ) (pour le gaz parfait )
Processus isentropique du gaz parfait
Le processus isentropique (un cas particulier du processus adiabatique) peut être exprimé avec la loi du gaz parfait comme:
pV κ = constant
ou
p 1 V 1 κ = p 2 V 2 κ
dans laquelle κ = c p / c v est le rapport des chaleurs spécifiques (ou capacités calorifiques ) pour le gaz. Un pour une pression constante (c p ) et un pour un volume constant (c v ) . Notez que ce rapport κ = c p / c v est un facteur déterminant la vitesse du son dans un gaz et d’autres processus adiabatiques.
Processus isochorique
Un processus isochore est un processus thermodynamique, dans lequel le volume du système fermé reste constant (V = const). Il décrit le comportement du gaz à l’intérieur du conteneur, qui ne peut pas être déformé. Étant donné que le volume reste constant, le transfert de chaleur dans ou hors du système ne fonctionne pas avec le p∆V , mais modifie uniquement l’ énergie interne (la température) du système.
Processus isochorique et première loi
La forme classique de la première loi de la thermodynamique est l’équation suivante:
dU = dQ – dW
Dans cette équation, dW est égal à dW = pdV et est connu comme le travail aux limites . Alors:
dU = dQ – pdV
Dans le processus isochore et le gaz parfait , toute la chaleur ajoutée au système sera utilisée pour augmenter l’énergie interne.
Processus isochorique (pdV = 0):
dU = dQ (pour le gaz parfait)
dU = 0 = Q – W → W = Q (pour le gaz parfait)
Processus isochorique du gaz parfait
Le processus isochore peut s’exprimer avec la loi du gaz parfait comme:
ou
Sur un diagramme pV , le processus se produit le long d’une ligne horizontale qui a l’équation V = constante.
Voir aussi: Loi de Guy-Lussac
Processus isobare
Un processus isobare est un processus thermodynamique , dans lequel la pression du système reste constante (p = const). Le transfert de chaleur dans ou hors du système fonctionne, mais modifie également l’énergie interne du système.
Puisqu’il y a des changements d’ énergie interne (dU) et des changements de volume du système (∆V), les ingénieurs utilisent souvent l’ enthalpie du système, qui est définie comme:
H = U + pV
Processus isobare et première loi
La forme classique de la première loi de la thermodynamique est l’équation suivante:
dU = dQ – dW
Dans cette équation, dW est égal à dW = pdV et est connu comme le travail aux limites . Dans un procédé isobare et le gaz parfait, une partie de la chaleur ajoutée au système sera utilisée pour faire le travail et une partie de la chaleur ajoutée augmentera l’ énergie interne (augmentera la température). Par conséquent, il est commode d’utiliser l’ enthalpie au lieu de l’énergie interne.
Processus isobare (Vdp = 0):
dH = dQ → Q = H 2 – H 1
À entropie constante , c’est-à-dire dans un processus isentropique, le changement d’enthalpie est égal au travail de processus d’écoulement effectué sur ou par le système.
Processus isobare du gaz parfait
Le processus isobare peut s’exprimer avec la loi du gaz parfait comme:
ou
Sur un diagramme pV , le processus se produit le long d’une ligne horizontale (appelée isobare) qui a l’équation p = constante.
Voir aussi: Charles’s Law
……………………………………………………………………………………………………………………………….
Cet article est basé sur la traduction automatique de l’article original en anglais. Pour plus d’informations, voir l’article en anglais. Pouvez vous nous aider Si vous souhaitez corriger la traduction, envoyez-la à l’adresse: translations@nuclear-power.com ou remplissez le formulaire de traduction en ligne. Nous apprécions votre aide, nous mettrons à jour la traduction le plus rapidement possible. Merci