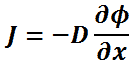Quel est le nombre de Schmidt
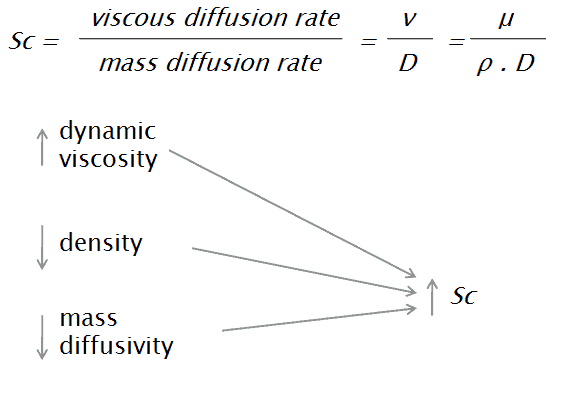
Le nombre de Schmidt est un nombre sans dimension, du nom de l’ingénieur allemand Ernst Heinrich Wilhelm Schmidt (1892-1975). Le nombre de Schmidt est défini comme le rapport de la diffusivité du moment (viscosité cinématique) et de la diffusivité de la masse . Il est utilisé pour caractériser les écoulements de fluide dans lesquels se produisent simultanément des processus de convection par diffusion du moment et de la masse. Le nombre de Schmidt décrit le transfert de masse en masse, et les équations peuvent être vues ci-dessous:
où:
- ν est la diffusivité du moment (viscosité cinématique) [m 2 / s]
- μ est la viscosité dynamique [Ns / m 2 ]
- D est la diffusivité de masse [m 2 / s]
- ρ est la densité [kg / m 3 ]
Il relie physiquement l’épaisseur relative de la couche hydrodynamique et de la couche limite de transfert de masse. Le nombre de Schmidt correspond au nombre de Prandtl en transfert de chaleur. Un nombre d’unité de Schmidt indique que le transfert de masse et d’impulsion par diffusion sont comparables, et que les couches limites de vitesse et de concentration coïncident presque les unes avec les autres. La diffusivité de masse ou le coefficient de diffusion est une constante de proportionnalité entre le flux molaire dû à la diffusion moléculaire et le gradient de concentration de l’espèce (ou la force motrice de diffusion). La diffusion de masse dans les liquides augmente avec la température, variation de viscosité inversement proportionnelle à la température, de sorte que le nombre de Schmidt, Sc = ν / D, diminue rapidement avec la température. Par exemple, le coefficient de diffusion de l’éthanol dans l’eau est D éthanol, eau = 1,6 × 10 – 9 et donne le nombre de Schmidt Sc = 540, ce qui est typique pour les liquides.
La loi de Fick énonce la diffusivité:
Si la concentration d’un soluté dans une région est supérieure à celle d’une autre solution, le soluté diffuse de la région à concentration supérieure à la région de concentration inférieure, avec une magnitude proportionnelle au gradient de concentration.
Dans une dimension (spatiale), la loi est:
où:
- J est le flux de diffusion,
- D est le coefficient de diffusion,
- φ (pour les mélanges idéaux) est la concentration.
L’utilisation de cette loi dans la théorie des réacteurs nucléaires conduit à l’ approximation de diffusion .
Nombre de Schmidt turbulent
De même que pour le nombre de Prandtl, le nombre de Schmidt a également une formule spéciale pour l’ écoulement turbulent . Le nombre de Schmidt turbulent décrit le rapport entre les taux de transport turbulent de la quantité de mouvement et le transport turbulent de la masse. Le nombre de Schmidt turbulent est couramment utilisé dans la recherche sur la turbulence et est défini comme:
Sc = ν t / K
où:
- ν t est la viscosité des tourbillons [m2 / s]
- K est la diffusivité des tourbillons [m2 / s]
……………………………………………………………………………………………………………………………….
Cet article est basé sur la traduction automatique de l’article original en anglais. Pour plus d’informations, voir l’article en anglais. Pouvez vous nous aider Si vous souhaitez corriger la traduction, envoyez-la à l’adresse: translations@nuclear-power.com ou remplissez le formulaire de traduction en ligne. Nous apprécions votre aide, nous mettrons à jour la traduction le plus rapidement possible. Merci