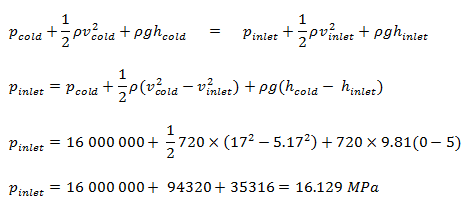Équation de Bernoulli
L’équation de Bernoulli peut être considérée comme une déclaration du principe de conservation de l’énergie approprié aux fluides en écoulement. C’est l’une des équations les plus importantes / utiles en mécanique des fluides . Il met en relation pression et vitesse dans un écoulement incompressible non invisible . L’équation de Bernoulli a quelques restrictions quant à son applicabilité, elles se résument comme suit:
- système à débit constant,
- la densité est constante (ce qui signifie également que le fluide est incompressible),
- aucun travail n’est fait sur ou par le fluide,
- aucune chaleur n’est transférée vers ou à partir du fluide,
- aucun changement ne se produit dans l’énergie interne,
- l’équation relie les états en deux points le long d’une même ligne de courant (pas de conditions sur deux lignes de courant différentes)
Dans ces conditions, l’équation d’énergie générale est simplifiée pour:
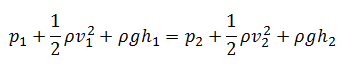
Cette équation est l’équation la plus célèbre de la dynamique des fluides . L’équation de Bernoulli décrit le comportement qualitatif du fluide en écoulement qui est habituellement désigné par le terme effet de Bernoulli . Cet effet provoque une baisse de la pression du fluide dans les régions où la vitesse d’écoulement est augmentée. Cet abaissement de la pression dans l’étranglement d’un chemin d’écoulement peut sembler contre-intuitif, mais moins quand on considère la pression comme une densité d’énergie. Dans le flux à grande vitesse à travers la constriction, l’énergie cinétique doit augmenter aux dépens de l’énergie de pression. Les dimensions des termes de l’équation sont l’énergie cinétique par unité de volume.
L’effet de Bernoulli – Relation entre pression et vitesse
Il s’agit d’un exemple illustratif, les données suivantes ne correspondent à aucune conception de réacteur.
Lorsque l’ équation de Bernoulli est combinée avec l’ équation de continuité, les deux peuvent être utilisées pour trouver des vitesses et des pressions à des points du flux reliés par une ligne de courant.
L’équation de continuité est simplement une expression mathématique du principe de conservation de la masse . Pour un volume de contrôle qui a une seule entrée et une seule sortie , le principe de conservation de la masse stipule que, pour un débit en régime permanent , le débit massique dans le volume doit être égal au débit massique sortant.
Exemple:
Déterminer la pression et la vitesse à l’ intérieur d’une branche froide de la tuyauterie primaire et déterminer la pression et la vitesse au fond d’un cœur de réacteur , qui est à environ 5 mètres en dessous de la branche froide de la tuyauterie primaire.
Supposons:
- Un fluide de densité constante ⍴ ~ 720 kg / m 3 (à 290 ° C) s’écoule régulièrement à travers la jambe froide et à travers le fond du cœur.
- La section transversale du débit de la tuyauterie primaire (boucle unique) est égale à 0,385 m 2 (diamètre de la tuyauterie ~ 700 mm)
- La vitesse d’écoulement dans la jambe froide est égale à 17 m / s .
- La section efficace d’écoulement du cœur du réacteur est égale à 5 m 2 .
- La pression manométrique à l’intérieur de la jambe froide est égale à 16 MPa .
En raison du principe de continuité, la vitesse au fond du noyau est:
v entrée = v froid . Une tuyauterie / un noyau A = 17 x 1,52 / 5 = 5,17 m / s
En raison du principe de Bernoulli, la pression au fond du cœur (entrée du cœur) est:
……………………………………………………………………………………………………………………………….
Cet article est basé sur la traduction automatique de l’article original en anglais. Pour plus d’informations, voir l’article en anglais. Pouvez vous nous aider Si vous souhaitez corriger la traduction, envoyez-la à l’adresse: translations@nuclear-power.com ou remplissez le formulaire de traduction en ligne. Nous apprécions votre aide, nous mettrons à jour la traduction le plus rapidement possible. Merci
