Quel est le théorème de Bernoulli – Définition

Conservation d’énergie

Ce principe est généralement appelé principe de conservation de l’énergie et stipule que l’ énergie totale d’un système isolé reste constante – on dit qu’elle est conservée dans le temps. Cela équivaut à la première loi de la thermodynamique , utilisée pour développer l’équation d’énergie générale en thermodynamique. Ce principe peut être utilisé dans l’analyse des fluides en écoulement et s’exprime mathématiquement par l’équation suivante: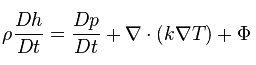où h est l’ enthalpie , k est la conductivité thermique du fluide, T est la température et est la fonction de dissipation visqueuse.

Théorème de Bernoulli

Le théorème de Bernoulli  peut être considéré comme un énoncé du principe de conservation de l’énergie approprié pour les fluides en circulation. C’est l’une des équations les plus importantes / utiles en mécanique des fluides . Il met en relation la pression et la vitesse dans un écoulement incompressible non visqueux . L’équation de Bernoulli a quelques restrictions dans son applicabilité, elles sont résumées dans les points suivants:

• système à débit constant,
• la densité est constante (ce qui signifie également que le fluide est incompressible),
• aucun travail n’est effectué sur ou par le fluide,
• aucune chaleur n’est transférée vers ou depuis le fluide,
• aucun changement ne se produit dans l’énergie interne,
• l’équation relie les états en deux points le long d’une même ligne de courant (pas les conditions sur deux lignes de courant différentes)

Dans ces conditions, l’équation générale de l’énergie est simplifiée pour:

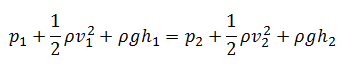
Cette équation est l’équation la plus connue en dynamique des fluides . L’équation de Bernoulli décrit le comportement qualitatif qui coule du fluide qui est généralement étiqueté avec le terme effet de Bernoulli . Cet effet provoque l’ abaissement de la pression du fluide dans les régions où la vitesse d’écoulement est augmentée. Cette baisse de pression dans une constriction d’un chemin d’écoulement peut sembler contre-intuitive, mais elle l’est moins quand on considère la pression comme étant la densité d’énergie. Dans le flux à grande vitesse à travers la constriction, l’énergie cinétique doit augmenter aux dépens de l’énergie de pression. Les dimensions des termes dans l’équation sont l’énergie cinétique par unité de volume.