Facebook Instagram Youtube Twitter

What is Bernoulli’s Effect – Relation between Pressure and Velocity – Definition

by
Bernoulli’s Effect – Relation between Pressure and Velocity. In this example flow rates through reactor and through primary reactor piping is calculated. Thermal Engineering

Bernoulli’s Equation

Bernoulli Equation; PrincipleThe Bernoulli’s equation can be considered to be a statement of the conservation of energy principle appropriate for flowing fluids. It is one of the most important/useful equations in fluid mechanics. It puts into a relation pressure and velocity in an inviscid incompressible flow. Bernoulli’s equation has some restrictions in its applicability, they summarized in following points:

  • steady flow system,
  • density is constant (which also means the fluid is incompressible),
  • no work is done on or by the fluid,
  • no heat is transferred to or from the fluid,
  • no change occurs in the internal energy,
  • the equation relates the states at two points along a single streamline (not conditions on two different streamlines)

Under these conditions, the general energy equation is simplified to:

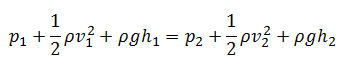
Bernoulli Theorem - Equation
This equation is the most famous equation in fluid dynamics. The Bernoulli’s equation describes the qualitative behavior flowing fluid that is usually labeled with the term Bernoulli’s effect. This effect causes the lowering of fluid pressure in regions where the flow velocity is increased. This lowering of pressure in a constriction of a flow path may seem counterintuitive, but seems less so when you consider pressure to be energy density. In the high velocity flow through the constriction, kinetic energy must increase at the expense of pressure energy. The dimensions of terms in the equation are kinetic energy per unit volume.

Bernoulli’s Effect – Relation between Pressure and Velocity

It is an illustrative example, following data do not correspond to any reactor design.

Continuity Equation - Flow Rates through Reactor
Example of flow rates in a reactor. It is an illustrative example, data do not represent any reactor design.

When the Bernoulli’s equation is combined with the continuity equation the two can be used to find velocities and pressures at points in the flow connected by a streamline.

The continuity equation is simply a mathematical expression of the principle of conservation of mass. For a control volume that has a single inlet and a single outlet, the principle of conservation of mass states that, for steady-state flow, the mass flow rate into the volume must equal the mass flow rate out.

Example:

Determine pressure and velocity within a cold leg of primary piping and determine pressure and velocity at a bottom of a reactor core, which is about 5 meters below the cold leg of primary piping.

Let assume:

  • Fluid of constant density ⍴ ~ 720 kg/m3 (at 290°C) is flowing steadily through the cold leg and through the core bottom.
  • Primary piping flow cross-section (single loop) is equal to 0.385 m2 (piping diameter ~ 700mm)
  • Flow velocity in the cold leg is equal to 17 m/s.
  • Reactor core flow cross-section is equal to 5m2.
  • The gauge pressure inside the cold leg is equal to 16 MPa.

As a result of the Continuity principle the velocity at the bottom of the core is:

vinlet =  vcold . Apiping / Acore = 17 x 1.52 / 5 = 5.17 m/s

As a result of the Bernoulli’s principle the pressure at the bottom of the core (core inlet) is:

Bernoulli Principle - Example

 
References:
Reactor Physics and Thermal Hydraulics:
  1. J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
  2. J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
  3. W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
  4. Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
  5. Todreas Neil E., Kazimi Mujid S. Nuclear Systems Volume I: Thermal Hydraulic Fundamentals, Second Edition. CRC Press; 2 edition, 2012, ISBN: 978-0415802871
  6. Zohuri B., McDaniel P. Thermodynamics in Nuclear Power Plant Systems. Springer; 2015, ISBN: 978-3-319-13419-2
  7. Moran Michal J., Shapiro Howard N. Fundamentals of Engineering Thermodynamics, Fifth Edition, John Wiley & Sons, 2006, ISBN: 978-0-470-03037-0
  8. Kleinstreuer C. Modern Fluid Dynamics. Springer, 2010, ISBN 978-1-4020-8670-0.
  9. U.S. Department of Energy, THERMODYNAMICS, HEAT TRANSFER, AND FLUID FLOW. DOE Fundamentals Handbook, Volume 1, 2 and 3. June 1992.

See also:

Bernoulli’s Principle

We hope, this article, Bernoulli’s Effect – Relation between Pressure and Velocity, helps you. If so, give us a like in the sidebar. Main purpose of this website is to help the public to learn some interesting and important information about thermal engineering.

Related Posts